Surface Area
Volume
Similar Solids
Mystery
100
Find the exact surface area of the cylinder (in terms of pi).
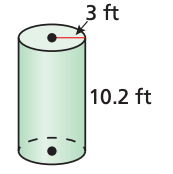
79.2pi
100
Find the exact volume of the oblique cylinder.
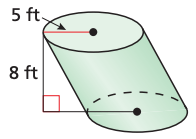
200pi
100
If the scale factor between the radii of two similar cylinders is k=3, what is the ratio of their volumes?
27:1
100
Name the shape of the cross section formed by the intersection of the plane and the solid.
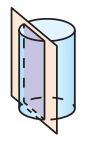
Rectangle
200
Find the exact surface area of the cone (in terms of pi).
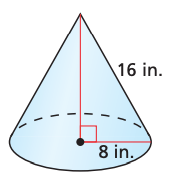
192pi
200
Given the volume of the prism below, find the unknown length 'w'.
w=4
200
The two prisms shown are similar. Find the value of 'x'.
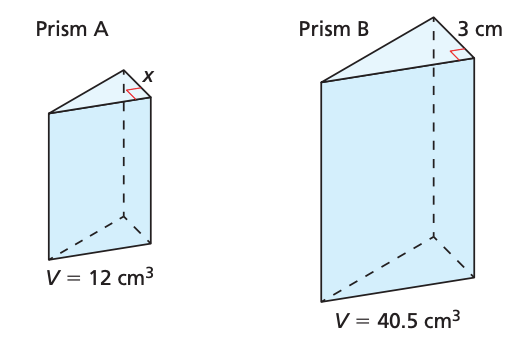
x=2
200
The 2D shape shown will be rotated 360 degrees about the vertical axis. Name and find the volume of the resulting solid (leave answer as simplified fraction).
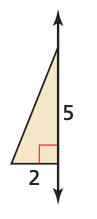
Cone.
V=(20pi)/3
300
Find the exact surface area of the hemisphere (simplified fraction in terms of pi).
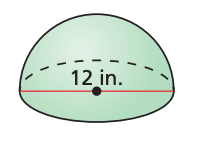
108pi
300
Find the exact volume of the hemisphere (simplified fraction in terms of pi).
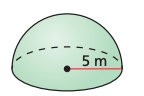
(250pi)/3
300
The two cones are similar. Find the exact volume of Cone B (simplified fraction in terms of pi).
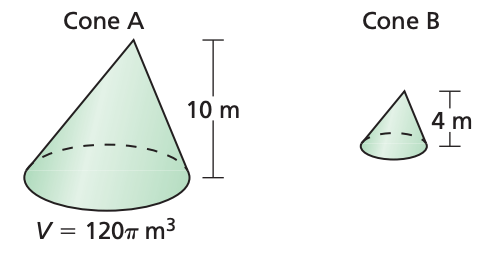
(192pi)/25
300
The 2D figure shown below will be rotated 180 degrees about the horizontal axis. Name the resulting 3D shape, and find its surface area.
Hemisphere.
147pi
400
Find the surface area of the square pyramid shown below.
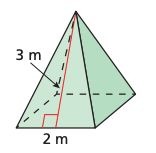
16
400
Find the exact volume of the cone (simplest radical form in terms of pi).
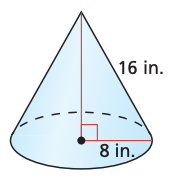
(512pisqrt3)/3
400
The two solids shown are similar. Find the height of Cylinder B.
h=10
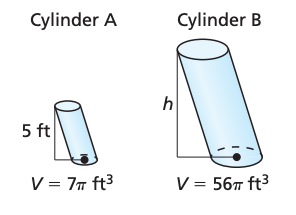
400
Completely simplify and factor the following expression.
pir^2+(2pir)/(2pil)*pil^2
pir(r+l)
500
Find the exact surface area of the composite solid shown below (simplest radical form, in terms of pi).
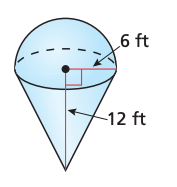
72pi+36pisqrt5
500
Find the exact volume of the composite solid.
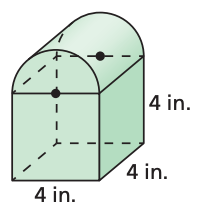
64+8pi
500
The two hexagonal pyramids shown below are similar. What is the ratio of their surface areas?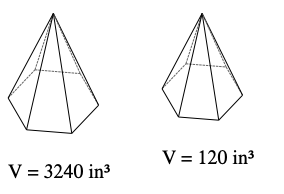
9:1
500
The two white circles are congruent and tangent to each other at the center of the blue circle. Find the ratio of the shaded region to the unshaded region.
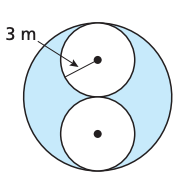
1:1