True or False: Volume is the amount of space that an object takes up.
True.
What is the area of this rectangle?
3 x 5 = 15 cm2
What is the formula for finding the volume of a rectangular prism?
Volume = length x width x height
or
Volume = Area of base x height
4 x (3 + 7) =
4 x 10 = 40
Why would filling a box with marbles and filling the same box with cubes be different amounts?
Sample answer:
They are different sizes and shapes. Marbles don't fit together as nicely as cubes.
Volume is measured in
A. Lines
B. Squared units
C. Cubic units
C
Area = length x width
I made a tower in the shape of a rectangular prism out of blocks. The length was 8 in, width was 2 in, and height was 4 in. What was the volume of the figure?
8x2x4 = 64 cubic inches
(4 x 3) + 7 =
12 + 7 = 19
Write an expression to show how you could play the following cards in Name That Number:
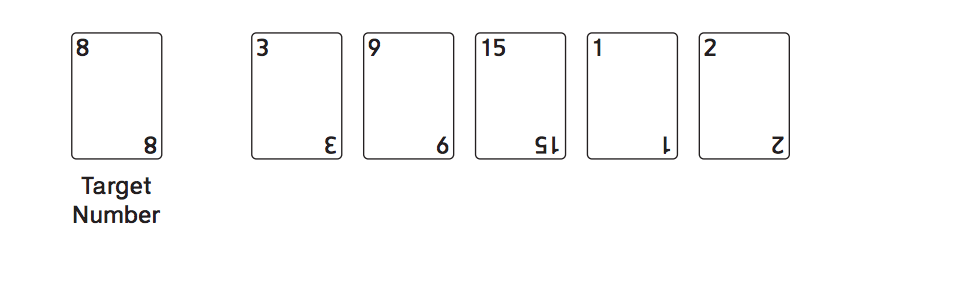
Sample answers:
2 x (3 + 1)
15 - 9 + 2 x 1
(15 + 1) / 2
The formula for volume of a rectangular prism is:
volume = length x width x height
What is the area of this rectangle?
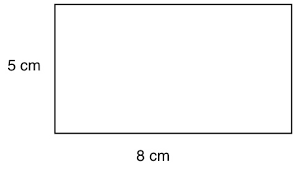
5 x 8 = 40 cm2
What is the volume of this figure?
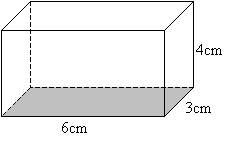
6 x 3 x 4 = 72 cm3
____ = (30 / 2 ) + 3
18 = 15 + 3
How many squares with the side of 1/7 inch would fit into 1 square inch?
1/7 x 1/7 = 1/49
49 squares
Centimeters x centimeters x centimeters = ?
cubic centimeters, or centimeters cubed, or cm3
Which ONE of the following demonstrates area?
- a kleenex box
- the top of a desk
- a line
The top of a desk
A box is 9 inches by 11 inches by 8 inches. What is the volume of the box?
792 cubic inches
____ = 30 / (2 + 3)
6 = 30 / 5
What is the volume of this prism?
4 x 6 x 3 = 72 units3
True or False: Another formula for volume is Area of the base x height.
True
What is the area of this rectangle?
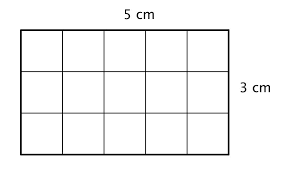
5 x 3 = 15 cm2
What is the volume of this prism?
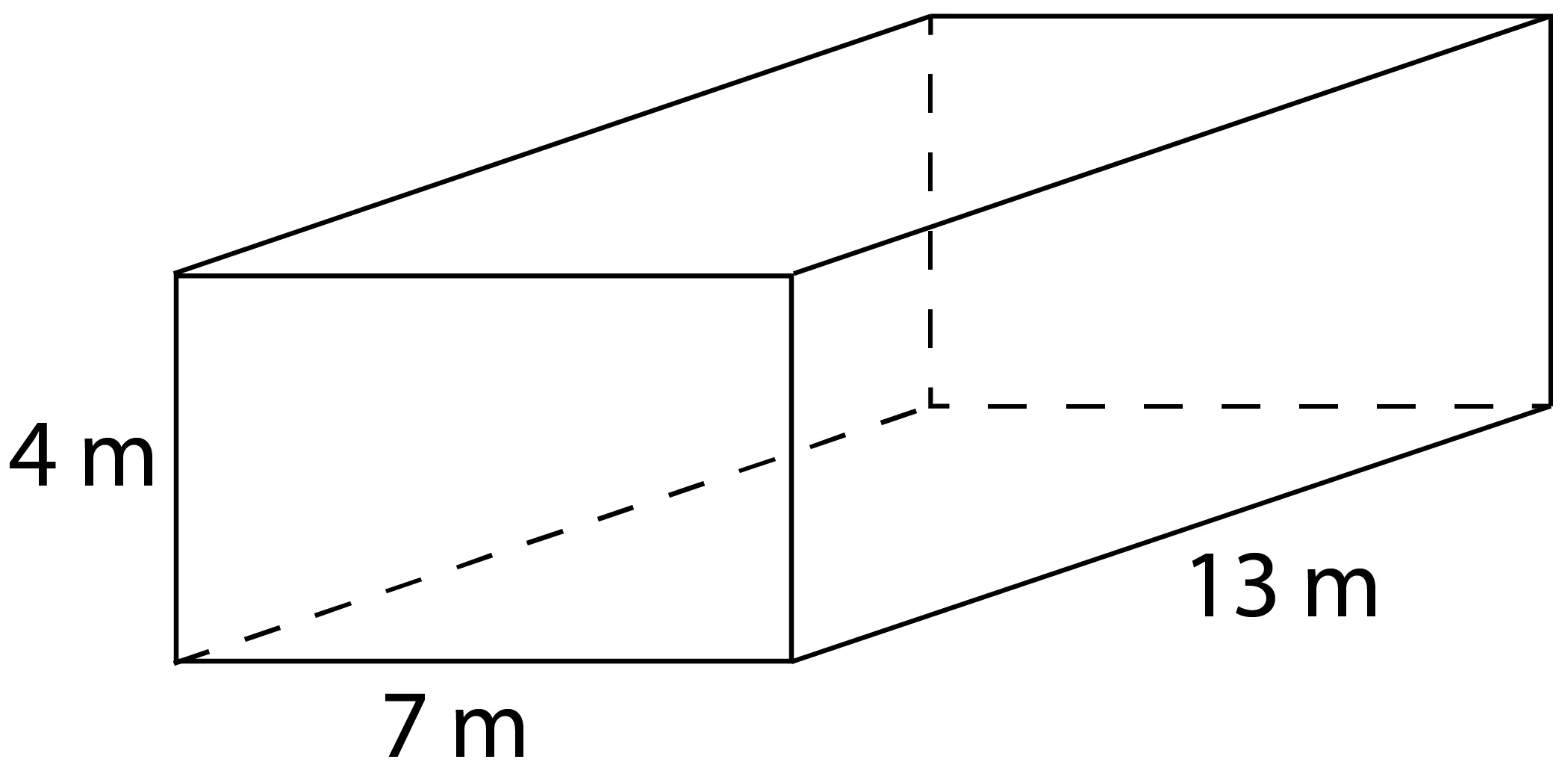
364m
Miss Wolf had $23. She Earned $7 more dollars. She donated half the money to the food bank. Write an expression that models the amount of money Miss Wolf donated.
(23 + 7) / 2
What is the volume of this figure?
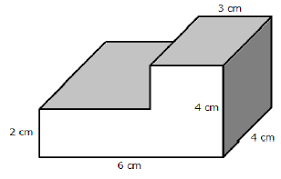
A = 4 x 6 x 2 = 48
B = 4 x 3 x 2 = 24
48 + 24 = 72 cm3