Write using fractional exponents:
root(4)22
22^(1/4)
Write using radicals:
5^(1/3)
root(3)(5)
Evaluate:
root(4)(625)^3
125
Given
f(x)=3x^2
and
g(x)=x^(1/3)+1
find
f(x)-g(x)
3x^2-x^(1/3)-1
Given
(3x^2)
and
g(x)=x^(1/3)+1
find
f(g(x))
3(x^(1/3)+1)^2
Write using fractional exponents:
(root(3)13)^2
13^(2/3)
Write using radicals:
10^(2/5)
root(5)(10^2)
Evaluate:
root(2)(100)^6
1000000
Given
(3x^2)
and
g(x)=x^(1/3)+1
find
f(x)/g(x)
(3x^2)/(x^(1/3)+1)
Given
(3x^2)
and
g(x)=x^(1/3)+1
find
g(f(x))
(3x)^(1/3)+1
Write using fractional exponents:
1/sqrt(17^5)
17^(-5/2)
Write using radicals:
2^(-5/9)
1/root(9)2^5
Evaluate:
4096^(5/4)
32768
Given
(3x^2)
and
g(x)=x^(1/3)+1
find the domain of
f(x)/g(x)
x!=-1
Using the table below, find f(g(1)) and g(g(1)).
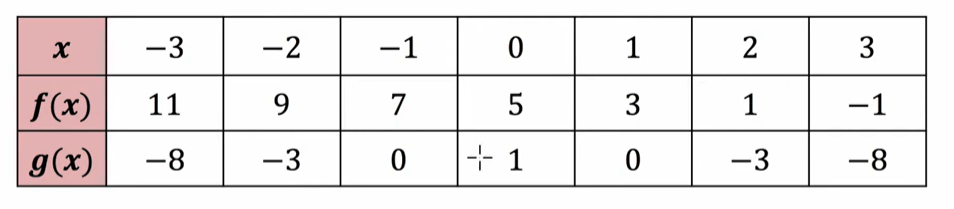
5 and 1
Write using fractional exponents:
root(2)((root(7)11)^9)
11^(9/14)
Write using radicals:
(5^(2/3))^(3/7)
root(7)(5^2)
Evaluate:
125^(1/3)root(6)(729)^2
45
Given
(3x^2)
and
g(x)=x^(1/3)+1
find the domain of
g(x)/f(x)
x!=0
Using the table below, find f(g(f(2)))
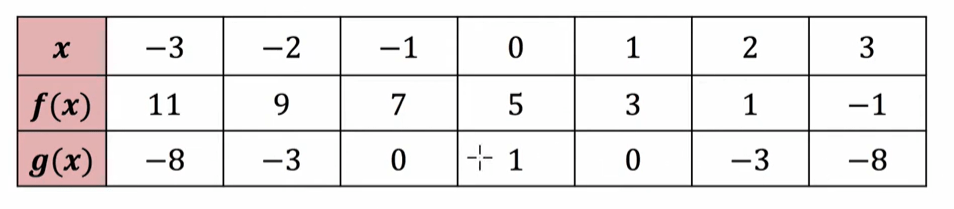
5
Explain why a "1st root" isn't written using a radical.
A "1st root" would just be x, or
x^(1/1)
What algebraic property says that
root(3)(5^2)=root(3)5^2
Commutative property
root(8)(6561)
3
Given a function f(x) with a domain of all real numbers, and a function g(x) with domain
x!=4
What do you know about the domain of
f(x)+g(x)
The domain is
x!=4
-9