Write the prime factorization of 42.
Break 42 down into 6 times 7.
7 is prime and 6 is not. 6 can be broken down into 2 times 3, which are both prime.
So the final answer is
2times3times7
Write the Greatest Common Factor of 30 and 60.
List all the factors of 30 and 60 first.
30: 1, 2, 3, 5, 6, 10, 15, 30.
60: 1, 2, 3, 4, 5, 6, 10, 15, 20, 30, 60.
The GCF is 30.
What is the LCM of 25 and 15
Write the multiples of each and find the first one they both share
15:15, 30, 45, 60, 75
25: 25,50,75
So 75 is the LCM
-2/5+8/5 in simplest form
1 1/5
2/5m=-12
m = -30
Write the prime factorization of 162.
162 is split into 2 times 81. 2 is prime. 81 is split into 9 times 9. 9 can be split into 3 times 3. That happens twice since 81 made 9 times 9. So we have
2times3^4
Find the GCF of 36 and 24.
List all the factors of 36 and 24 first.
36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
24: 1, 2, 3, 4, 6, 8, 12, 24.
The GCF is 12
Find the Least Common Multiple of 8 and 20.
Write the multiples of 8 and 20.
8: 8, 16, 24, 32, 40
20: 20, 40
So the LCM is 40
2 1/3-(-1 3/12)
3 7/12
x+2/5=-6/5
x=-8/5
Write the prime factorization of 120 in exponential form.
120 is split into 12 times 10. 12 is broken into 4 times 3 and that 4 is broken into 2 times 2. Now 10 is broken into 5 times 2 which are both prime. So the final answer is
2^3times 5times3
What does it mean when two or more numbers are "relatively prime?"
Give an example.
If their only common factor is 1, two or more numbers are relatively prime.
Examples include 3 and 4, or 7 and 15.
During a trip to the beach, Dan built sandcastles with 4 towers each, and Greg built sandcastles with 11 towers each. Before leaving, they counted the towers and realized that they had each built the same number. What is the smallest number of towers each must have built?
Find the LCM of the two numbers
4: 4,8,12,16,20,24,28.32.36,40,44
11:11,22,33,44
So 44 is the LCM
2 1/2 divide (-5/6)
-3
2/3n-4=3/5
6 9/10
Write the prime factorization of 300 in exponential form.
300 is split into 2 times 150. 2 is prime. 150 is split into 2 times 75. 75 is split into 3 times 25. 25 is split into 5 times 5.
Our final answer is
2^2times3times5^2
Find the Greatest Common Factor of 48 and 80.
List all the factors of 48 and 80 first.
48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
The GCF is 16.
Find the LCM of 42 and 80.
Find the prime factorization of 42
42: 2 × 3 × 7
Find the prime factorization of 80
80 = 2 × 2 × 2 × 2 × 5
Multiply each factor the greater number of times it occurs in steps i) or ii) above to find the LCM:
LCM = 2 × 2 × 2 × 2 × 3 × 5 × 7 = 1680
-3 4/5times5/6
-3 1/6
x/-3 +2/5=3/5
x=-3/5
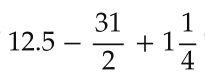
-7/4 or -1 3/4 or -1.75
Write the prime factorization of 192 in exponential form.
192 can be split into 3 times 64. 3 is prime and 64 can be divided into 8 times 8. Both of these are not prime and can be split into 2 and 4. 2 is prime and 4 is split into 2 times 2.
So we have
3 times 2 times 2 times 2times2times2times2
3times2^6
Find the GCF of 6, 14, and 28.
List the factors of each.
6: 1, 2, 3, 6
14:1, 2, 7, 14
28:1, 2, 4, 7, 14, 28
GCF is 2
Find the LCM of 50 and 72 through prime factorization
Find the prime factorization of 50
50 = 2 × 5 × 5
Find the prime factorization of 72
72 = 2 × 2 × 2 × 3 × 3
Multiply each factor the greater number of times it occurs in steps i) or ii) above to find the LCM:
LCM = 2 × 2 × 2 × 3 × 3 × 5 × 5
LCM = 1800
-4 1/6-1 3/4
-5 11/12
-3/4m-2 1/2=4 1/5
m=-8 14/15
Factor the following expression:
x^3+x^2+x^
x(x^2+x+1)