Equations and Inequalities
Unit Rate
Percents and Ratio
Geometry
Definitions
100
−6k − 13 = 83
k=-16
100
Amy drove to her mother’s house, which is 204 miles away. If it took her 3 hours, what was her average speed?
68 miles per hour
100
A roll of 40 quarters weighs 8 ounces. Which proportion can be used to find the weight in ounces, w, of 200 quarters?
A. 40/8 = 200/w
B. 40/w = 8/200
C. 40/200 = w/8
D. 40/8+w = w/200
A
100
Find the volume
168 m3
100
reciprocal
The inverse of a fraction
200
8x = -10x + 36
x = 2
200
Which is the best buy? 6 shirts for $25.50, 4 shirts for $18.00, or 5 shirts for $21
$21.00 / 5 shirts = $4.20 per shirt- this is the best buy
200
Bed, Bath and Beyond has a 20% off coupon. If I buy a towel normally priced $60, how much would I pay after using the coupon?
$48
200
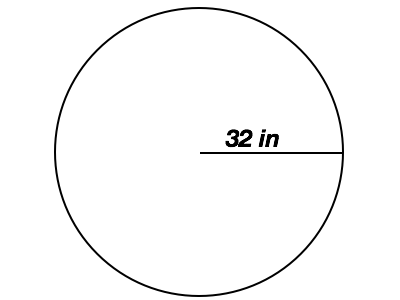
find the circumference
200.96 in
200
hypotenuse
The longest side of a right triangle. The side opposite the right angle
300
5(2x + 3) = 3(4x + 3) - 2(3x + 2)
x = -4
300
Jacky needs to ride her bike to her friend’s house 96 miles away. She is riding at an average rate of 15 miles per hour. She has 6 hours to get there. Will she make it?
No
300
In an election, 350 people voted for Class President. Asuman got 58% of the votes. How many votes did Asuman get?
203 votes
300
find the area of number 8
834.55 mm2
300
supplementary angles
two angles that add up to 180 degrees
400
7/10n+ 3/2 = 3/5n +2
n=5
400
Five lemons cost $1.80. What is the cost per lemon?
$0.36
400
If you start with $100, spend $32, but then return an item and get $7 back, what percent of your money do you still have?
75%
400
find the surface area
202 m2
400
complimentary angles
angles that add up to 90 degrees
500
12 + 5x - 8 = 12x - 10
x=2
500
Five lemons cost $1.80. At this rate, what is the cost of 9 lemons?
$3.24
500
A crew is made up of 8 men; the rest are women. 66% of the crew are men. How many people are in the crew?
12 people
500
What is the length of DE
2.25
500
adjacent
having a common boundary or edge