For the Box-Plot shown, state the range and IQR
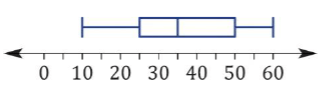
Range = 60 - 10 = 50
IQR = Q3 - Q1 = 50 - 25 = 25
Calculate the gradient of the line that connects (1, 8) and (3, 12)
m = (12-8)/(3-1) = 4/2 = 2
The triangle A(1,2), B(3,4), C(0,2) is reflected in the x-axis. State the coordinates of the image points A', B' and C'.
A' = (1,-2)
B' = (3,-4)
C' = (0,-2)
Determine if the following is a right-angled triangle:
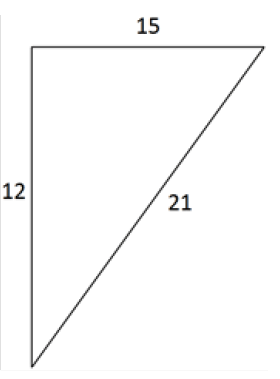
If right angled, then: c2 = a2 + b2
21^2 = 12^2 + 15^2
441 = 144 + 225
441 != 369
LHS != RHS
NOT a right-angled triangle
What date is your Semester test for Maths?
Thursday 24th November 2022
The data below represents the number of days students in class were absent from school this year. Represent it as a stem-and-leaf plot.
4 12 5 9 0 21 10 48 12

Find the equation of the line that is parallel to y = 2x +1 and passes through the point (1, 7).
Parallel means same gradient, so y = 2x + c.
Let x = 1, y = 7: 7 = 2x1 + c, so c = 5
So equation is y = 2x + 5
Given that the following triangles are similar, find the values of the pronumeral to 2 decimal places
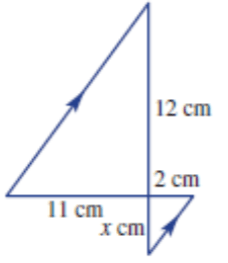
Scale Factor = Image / Original = 2/11
therefore x = 12 xx 2/11 = 24/11 = 2.18cm
The following word related to Pythagoras' Theorem is misspelled. State the correct spelling:
High-pott-and-yous
Hypotenuse
Name this song & artist:
Never Gonna Give You Up - Rick Astley
Consider the following values:
3, 33, 15, 8, 33, 47, 22
State the mean, median and mode
Mean = 23
Median = 22
Mode = 33
Find the coordinates of the x and y intercepts for the line with the rule 3x + 2y = 12
For x-int, let y = 0
3x + 0 = 12
x = 4
x-int is (4,0)
For y-int, let x = 0
0 + 2y = 12
y = 6
y-int is (0,6)
Heron's formula for the area, A, of a triangle with side lengths a, b and c is given by:
A=sqrt(s(s-a)(s-b)(s-c)) and s=(a+b+c)/2
Find A when a=3cm, b=4cm and c=5cm
s=(a+b+c)/2 = (3 + 4 + 5)/2 = 6
A=sqrt(s(s-a)(s-b)(s-c))
A = sqrt(6(6-3)(6-4)(6-5))
A = sqrt(6xx3xx2xx1) = sqrt(36) = 6cm^2
The following represent the 3 side lengths of 3 triangles. For each triangle, determine whether it is a right-angle triangle or not.
A: 8cm, 15cm, 17cm
B: 9m, 16m, 25m
C: 12cm, 13cm, 50mm
A: YES - Satisfies Pythagoras Theorem
B: NO - Does not satisfy Pythagoras Theorem
C: YES - Satisfies Pythagoras Theorem (after making units the same)
Combine the following numbers together using addition, subtraction, multiplication and division to reach the target number. Each number can be used only once. You do not need to use all numbers.
100, 9, 6, 2, 8, 5 TARGET: 538
Many solutions exist. Some possible combinations:
5x100 + 2x(9+6) + 8 = 500 + 30 + 8 = 538
5x(100+6) + 8 = 530 + 8 = 538
5x(100+8) - 2 = 540 - 2 = 538
etc.
Write down a set of 6 integers with the mean < median < mode, and range = 10
Many solutions exist. One example:
1, 6, 8, 10, 11, 11.
(Mean = 7.8, Median = 9, Mode = 11, Range = 10)
Find the equation of the following line:
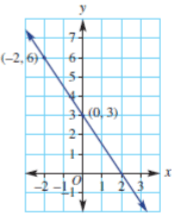
y = (-2)/3 x+3
Define the following triangles:
Equilateral, Isosceles, Scalene
BONUS: Which triangles can be right-angled?
Equilateral = All sides and angles are equal.
Isosceles = 2 sides are equal. 2 angles are equal.
Scalene = All sides and angles are different.
Right-Angled = A triangle where one of the internal angles is 90O. Therefore equilateral cannot be R-A (all angles 90O), isosceles can if the other two angles are 45O and scalene can if the other two angles are not 45O
Find the value of x, correct to 2 decimal places (if required):
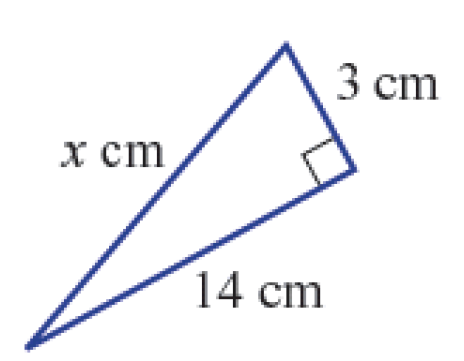
c^2 = a^2 + b^2
therefore x^2 = 14^2 + 3^2
therefore x^2 = 205
therefore x = sqrt(205)
x ~ 14.32cm
Recite pi to as many digits as you can. Most digits accurately remembered = 400 points, 2nd = 300 points, 3rd = 200 points, 4th = 100 points
pi =
3.1415 92653 58979 32384 62643 38327 95028 84197 16939 93751 05820 97494 45923 07816 40628 62089 98628 03482 53421 17067 9...
The following data represents the sale price of 10 houses in a Melbourne street. Calculate the upper and lower fences to determine if there are any outliers.
$510,000 $546,000 $560,000 $578,000 $595,000
$637,000 $693,000 $840,000 $952,000 $1,295,000
Min = 510,000, Q1 = 560,000, Med = 616,000 Q3 = 840,000, Max = 1,295,000, therefore IQR = Q3 - Q1 = 840,000 - 560,000 = $280,000
Lower Fence = Q1 - 1.5 x IQR = 560,000 - 1.5 x 280,000 = $140,000
Upper Fence = Q3 + 1.5 x IQR = 840,000 + 1.5 x 280,000 = $1,260,000
So $1,295,000 is an outlier because it is above the upper fence.
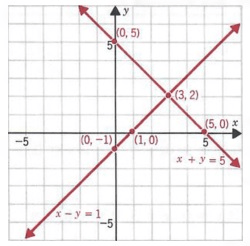
Sketch a graph of the following two lines on the same set of axes and find the coordinates of their intersection:
y = x - 1
y = -x + 5
Translated 3 units up, reflected in the y-axis, translated 4 units left then rotated 180o clockwise about the origin. What are the new coordinates of the corners of the square?
(-3, 1) -> (-3, 4) -> (3, 4) -> (-1, 4) -> (1, -4)
(2, 1) -> (2, 4) -> (-2, 4) -> (-6, 4) -> (6, -4)
(2, 6) -> (2, 9) -> (-2, 9) -> (-6, 9) -> (6, -9)
(-3, 6) -> (-3, 9) -> (3, 9) -> (-1, 9) -> (1, -9)
Find the value of the pronumeral in the following composite shape, correct to 2 decimal places. Then, find its area (also correct to 2dp).
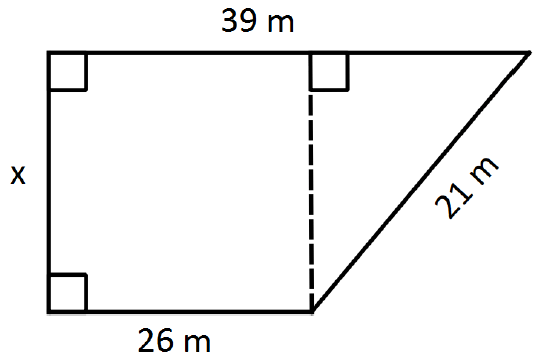
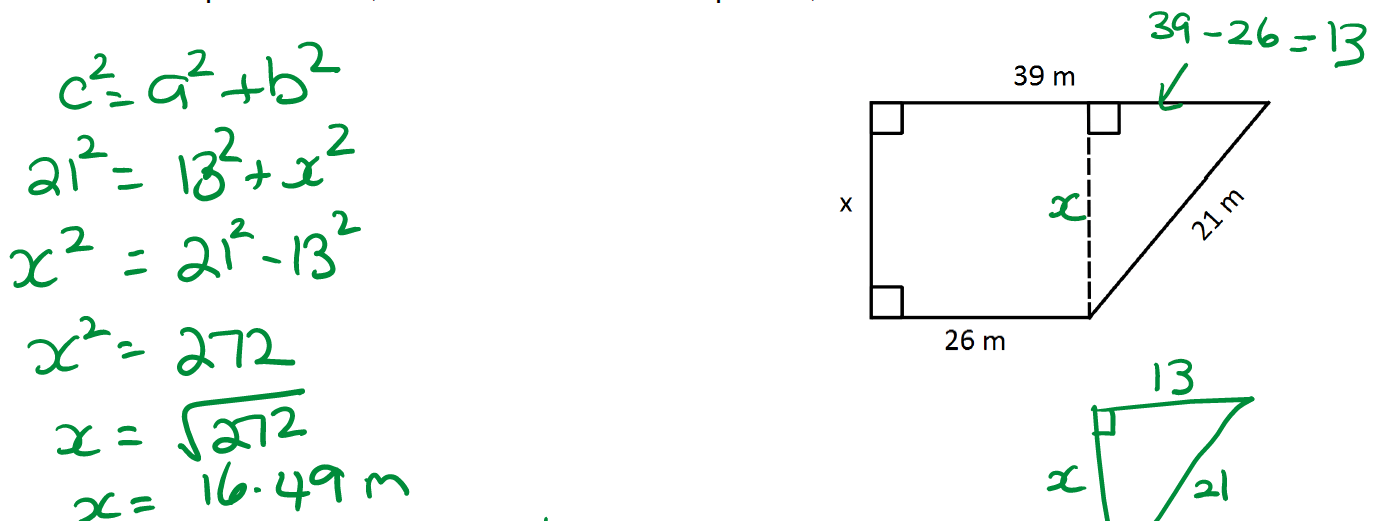
Area = Arectangle + Atriangle OR use Trapezium rule (A = (a+b)/2 x h)
A = (26+39)/2 xx sqrt(272) = 32.5 xx sqrt(272) = 536.00m^2 (allow 535.93m^2)
Name five year 8 maths teachers (100 points for each).
???