Rigid Transformations
Transformation Analysis
Congruence and Transversals
Similarity
Slope
100
Anika started with Figure A and performed two transformations, which resulted in the figures shown below.
Transformation 1 resulted in Figure B from Figure A. Transformation 2 resulted in Figure C from Figure B.
Describe each transformation.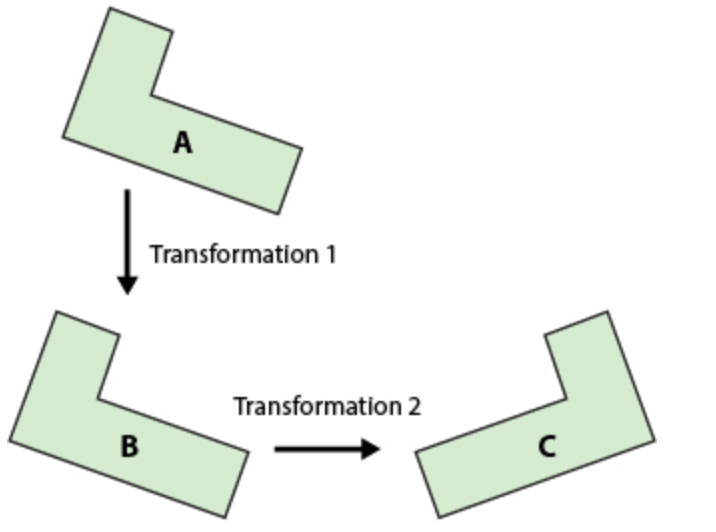
Transformation 1: Translation
Transformation 2: Reflection
100
The coordinate plane below shows the location of △RST.
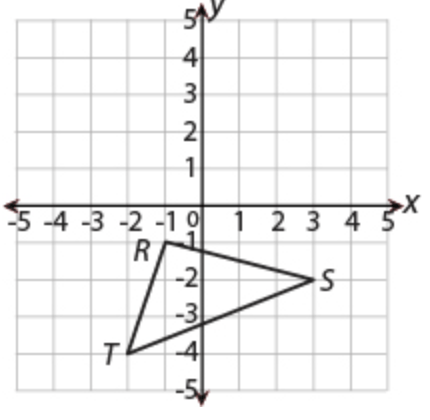
Triangle RST was rotated 90 degrees clockwise about the origin to form △R'S'T'. Which coordinate plane shows the location of △R'S'T'?
a.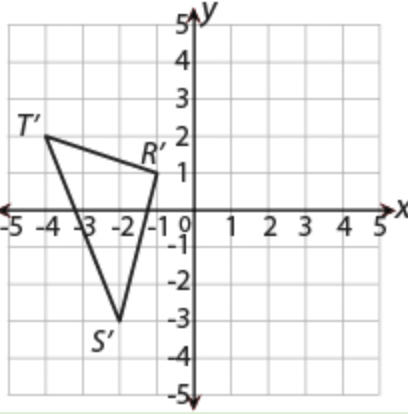 
b.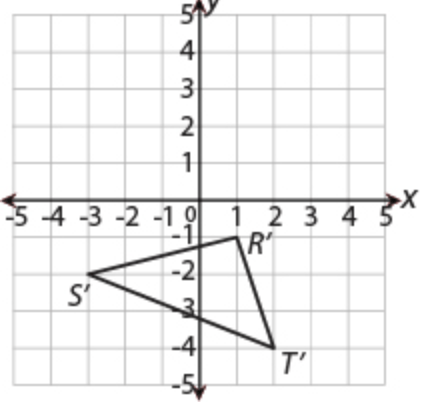 
c.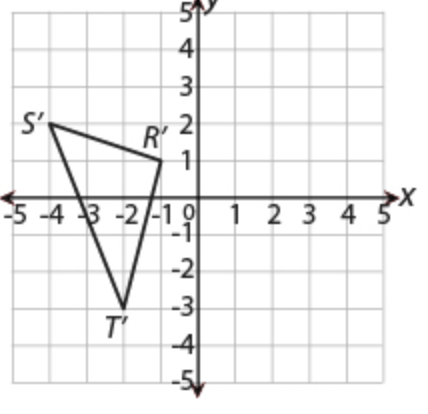 
A. 
100
What are the measurements of angle x and y?
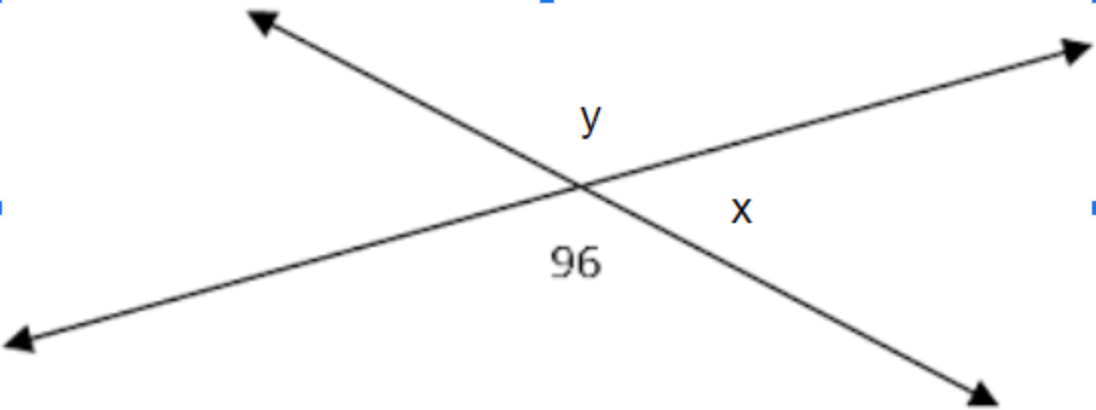
x = 84°
y = 96°
100
In the figure below, △ABC is similar to △DEF.
What is the measure of ∠F?
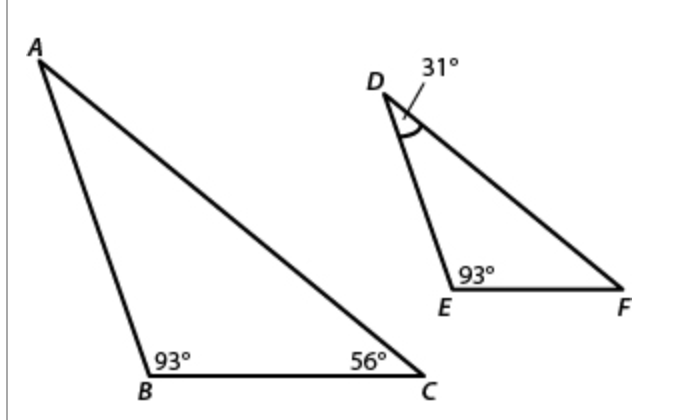
∠F = 56°
100
A line is graphed below.
What is the slope of the line?
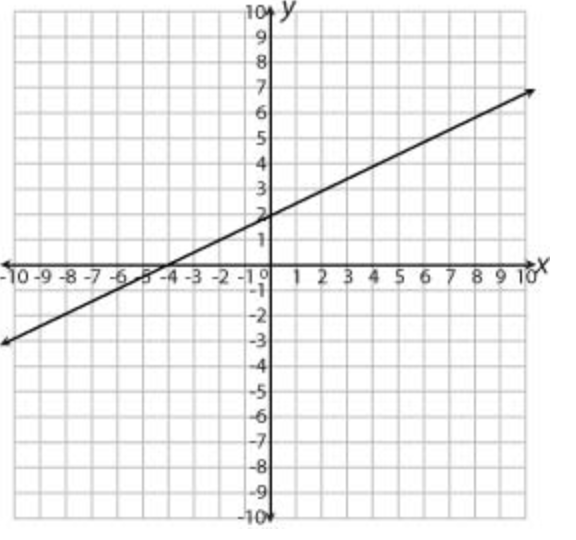
Slope = 1/2
200
A line segment is plotted on a coordinate plane with the end points at (–9,–5) and (–4,–5).
The line segment has been translated 12 units to the right and 9 units up. Graph the end points of the line segment after this translation.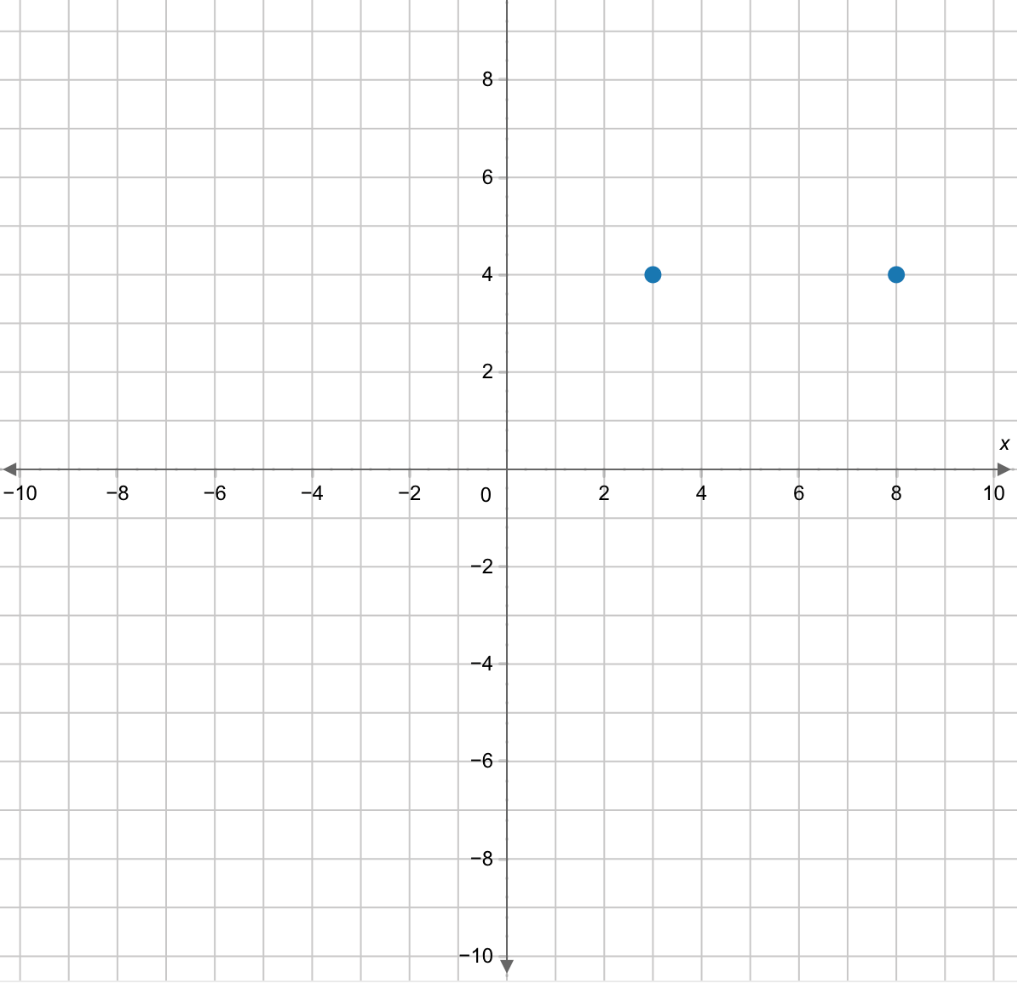
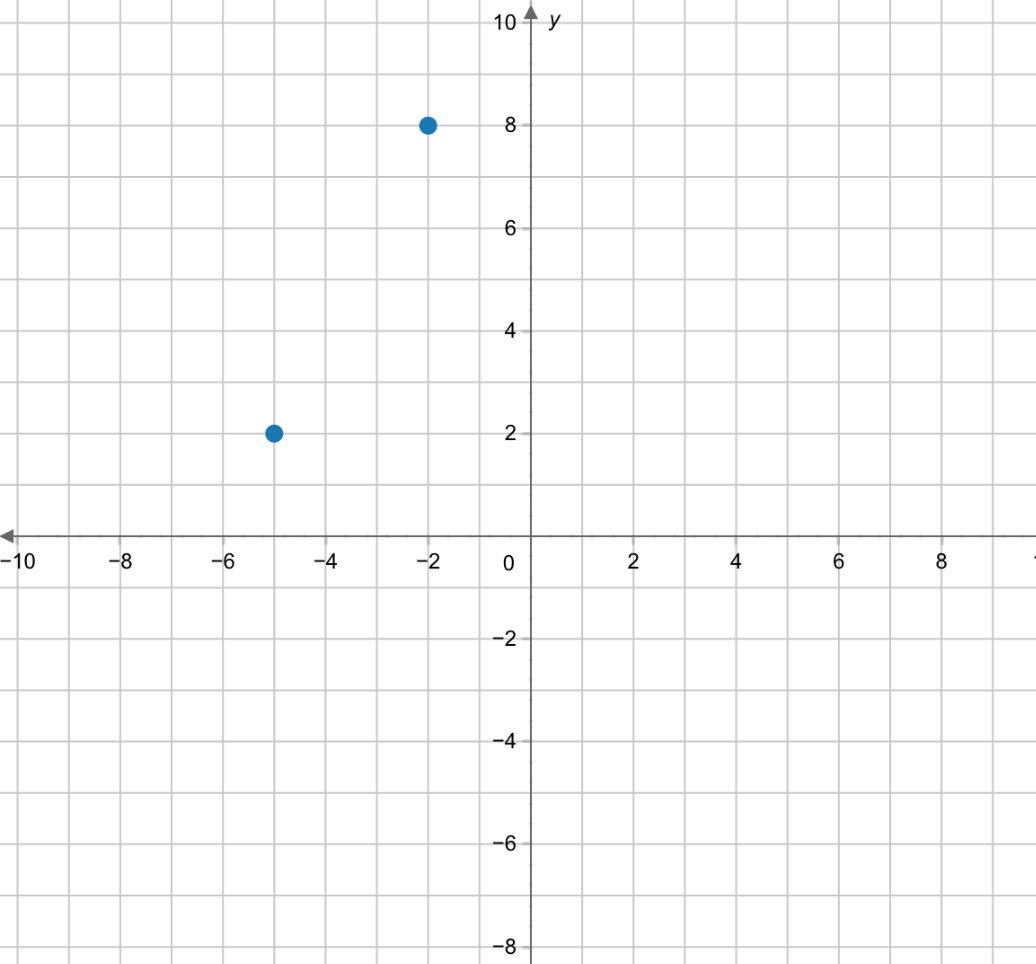
200
An angle graphed in the coordinate plane has a measure of 120°. Which of the following statements are true? Select TWO that apply.
A
After a reflection over the x-axis, the angle will still measure 120°.
B
After a translation 9 units down, the angle will no longer measure 120°.
C
After a 270°-clockwise rotation about the origin, the angle will no longer measure 120°.
D
After a 90°-counterclockwise rotation about the origin, the angle will still measure 120°.
E
After a dilation through the origin by a scale factor of 14, the angle will no longer measure 120°.
A.
Angle measures remain the same after a reflection.
D.
Angle measures remain the same after a rotation.
200
Triangle ABC is shown. The measure of the interior angle at point A is 29° and the exterior angle at point C is 82°.
What is the measure of angle x?
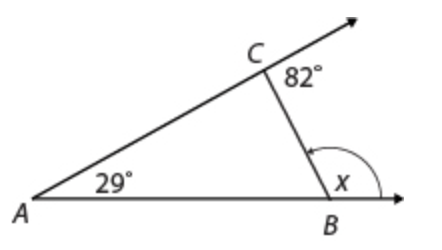
x = 127°
200
In the figure below, △MNO is similar to △PQR.
What is the measure of ∠N?
Complete the equation to show how to find the measure of ∠N. Type the response in the boxes below.
∠N = (_____) – (84 + _____) = ______°
180°
55.5°
40.5°
200
What is the formula for finding the slope of a line?
Rise divided by Run
Rise/Run
y/x
300
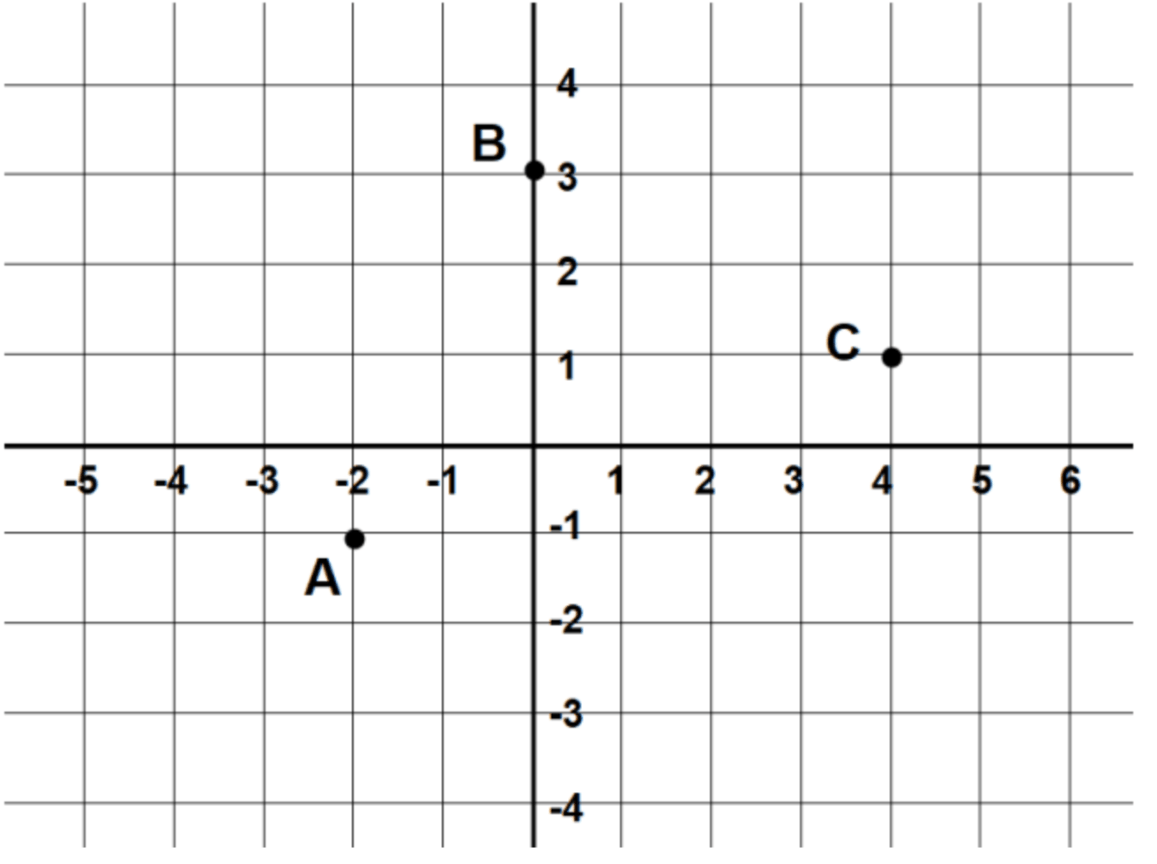
What are the coordinates of A, B, and C after a translation 1 unit to the left and 3 units down?
A' (-3, -4) B' (-1, 0) C' (3, -2)
300
In the figure below △A′B′C′ is the image of △ABC after two transformations are applied.
Describe the transformations that map △ABC to △A′B′C′.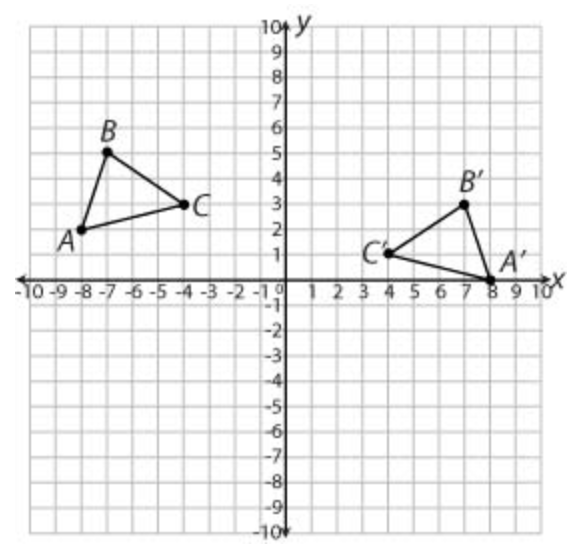
△A′B′C′ is the result of applying a translation two units down followed by a reflection across the y-axis to △ABC.
300
Describe a single transformation that takes triangle WIG onto triangle FLD. Be sure to include all key pieces of information necessary for the given transformation. How does this single transformation demonstrate that the triangles are the same, or congruent? (3 points)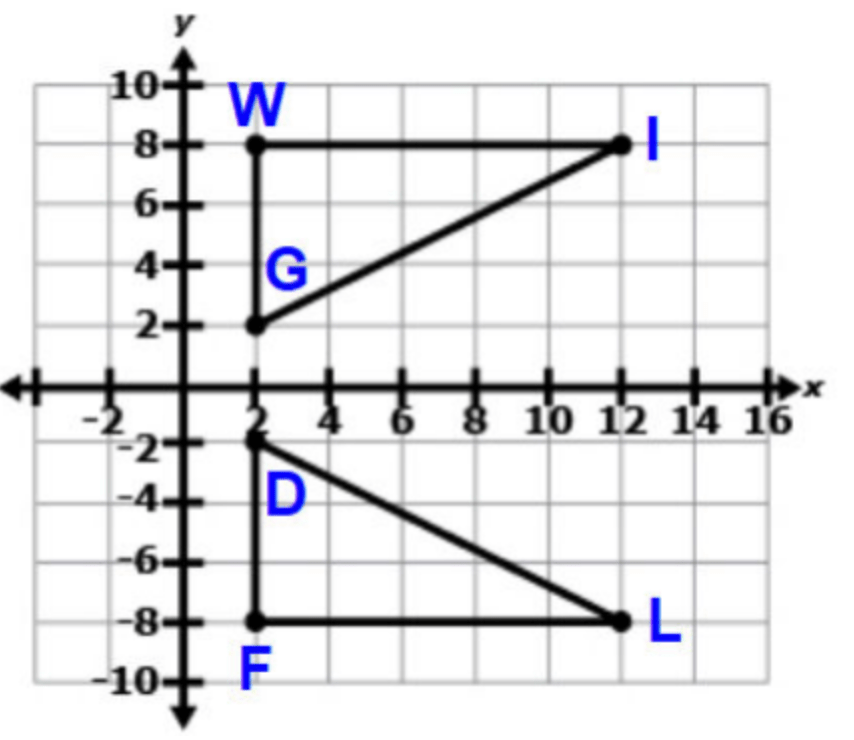
Reflection over the x-axis, and accurately described that the figures were congruent because all points of the triangle correspond to point in the other figure.
300
Figure ABCDE is rotated 180° and then translated down to form a figure with the listed angles.
Find all of the Angles in Figures ABCDE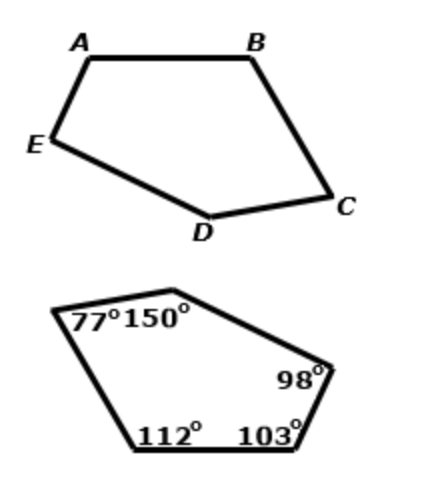
<A = 103°
<B = 112°
<C = 77°
<D = 150°
<E = 98°
300
A line is shown on the coordinate plane.
What is the equation of the line?
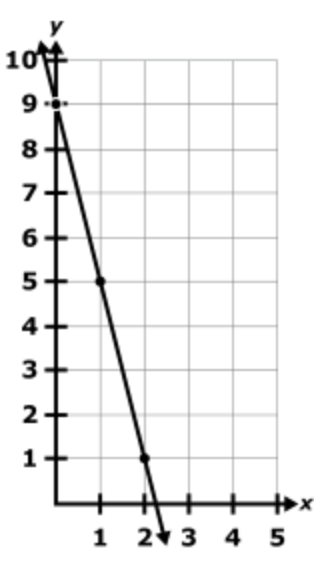
y = -4x + 9
400
On the graph, △DEF was transformed to create △DGH.
Which transformations show that △DEF is similar to △DGH?
A dilation by a scale factor of 3 and then a 180° rotation about the origin
400
What do you need to know to perform a:
Translation: ____________________
Reflection: ____________________
Rotation: ____________________
Dilation: ____________________
Translation: Distance and direction
Reflection: Line of Reflection
Rotation: Degree and Direction
Dilation: Scale Factor and Center of Dilation
400
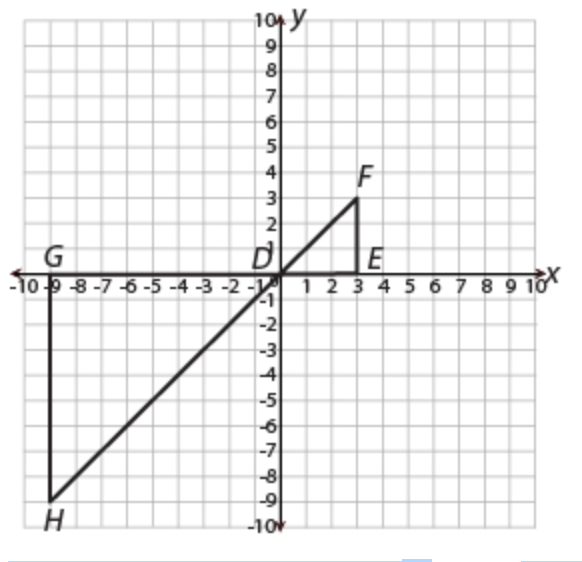
In the figure shown, lines k and l are parallel.
If the measure of < 7 = 100° , what is the measure of < 4?
<4 is 80°
400
These two triangles are similar triangles. If the smaller triangle is dilated to become the bigger triangle, what would the length of side x be?
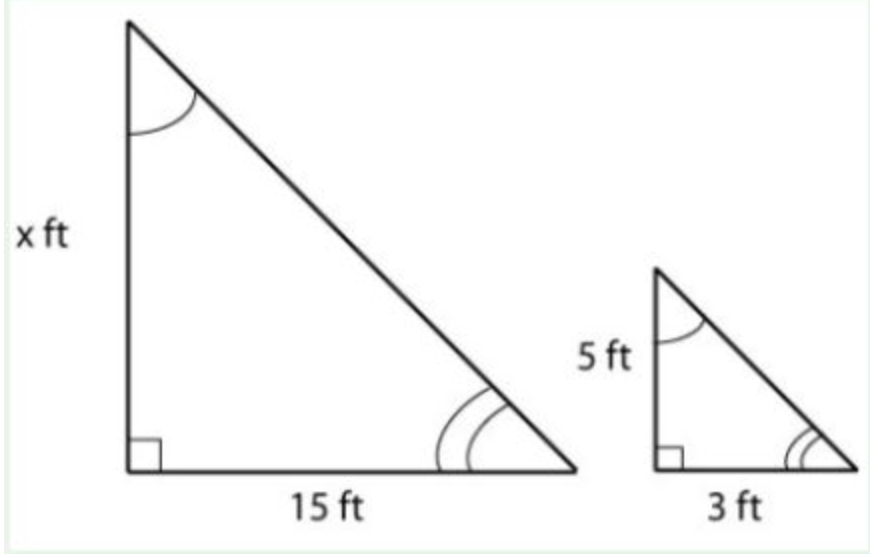
x = 25
400
Line t and ∆ACE and ∆BFD are shown on the coordinate plane.
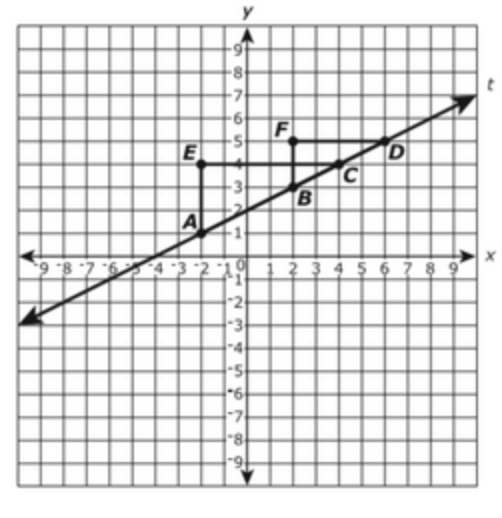
A. The slope of line AC is equal to the slope of line BC
B. The slope of line AC is equal to the slope of line BD
C. The slope of line AC is equal to the slope of line t
D. The slope of line t is equal to EC/AE
E. The slope of line t is equal to FB/FD
F. The slope of line t is equal to AE/FD
A. The slope of line AC is equal to the slope of line BC
B. The slope of line AC is equal to the slope of line BD
C. The slope of line AC is equal to the slope of line t
E. The slope of line t is equal to FB/FD
500
Which set of coordinates represents the reflection of the following image over the y–axis?
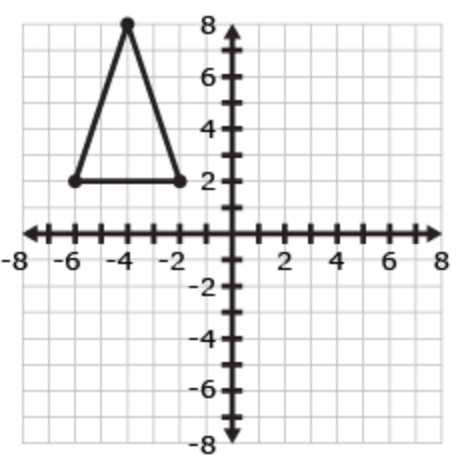
(6 , 2), (4 , 8), (2 , 2)
500
Figure 2 is a transformation of Figure 1, and vertex X is on line n.
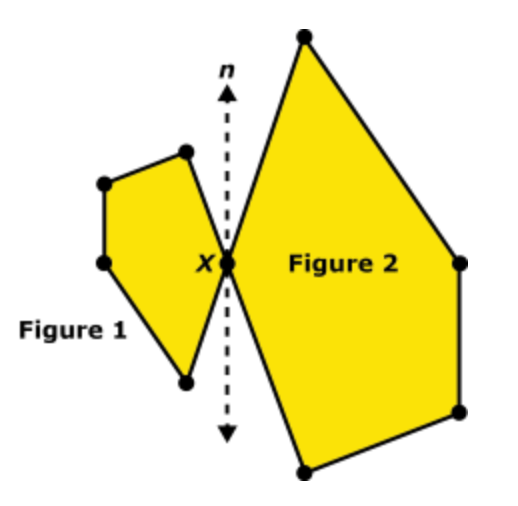A. a rotation of 180° counterclockwise about vertex X followed by a dilation through vertex X by scale factor greater than 1
B. a rotation of 180° counterclockwise about vertex X followed by a dilation through vertex X by scale factor less than 1
C. a reflection over line n followed by a dilation through vertex X by scale factor greater than 1
D. a reflection over line n followed by a dilation through vertex X by scale factor less than 1
A. a rotation of 180° counterclockwise about vertex X followed by a dilation through vertex X by scale factor greater than 1
500
Tiana has a triangular piece of construction paper. She cuts the paper into three pieces.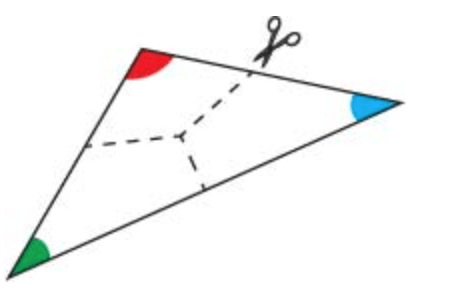
Then, she rearranges the three pieces as shown.
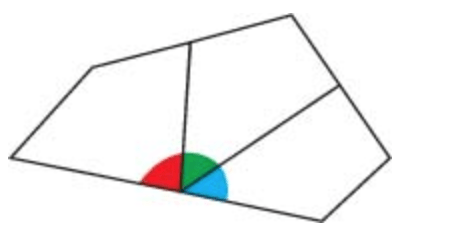
What do the pieces of Tiana's triangle show?
The sum of the interior angles of a triangle is equal to the measure of a straight angle.
500
Describe a sequence of transformations that shows that triangle A”B”C” is similar to A’B’C’. Include all necessary information to complete each transformation. Your response should include justification for similarity.
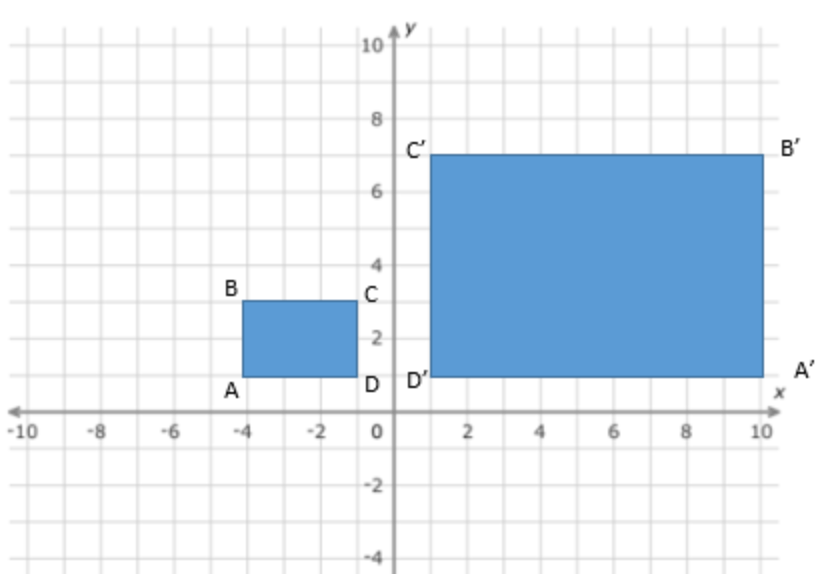
A reflection across the x- axis. A dilation of scale factor 3 from point (1, 1).
The two figures are similar because they are still the same shape, and after a series of transformations, including a dilation the sides are now proportional and the angles remain the same measures.
500
Grace drew two right triangles that have hypotenuses on the same line as shown in the coordinate plane below.
Part A: What is the slope of the hypotenuse of △ABC?
Part B: What is the slope of the hypotenuse of △AGH?
Part C: How do they compare?
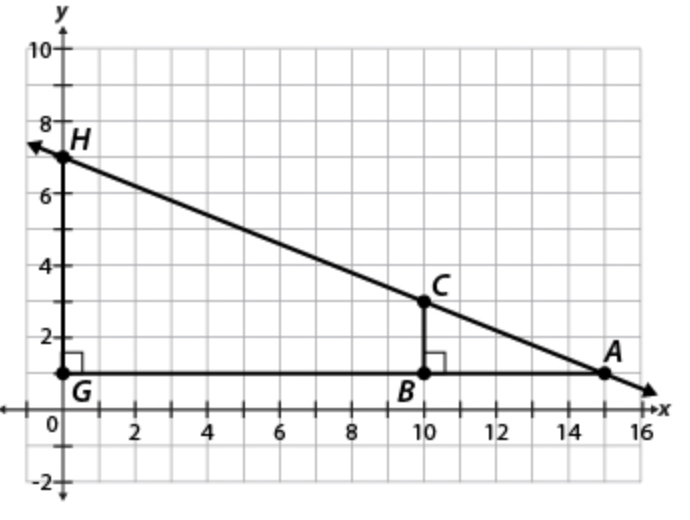
Part A: The slope of the hypotenuse of △ABC=−2/5
Part B: The slope of the hypotenuse of △AGH=−2/5
Part C: The slope of the hypotenuse of △ABC is the same as slope of the hypotenuse of △AGH.