Rigid Transformations
Dilations
Scale Factor
Congruence/ Similarity
Intro to Slope
100
What transformation is happening in this image?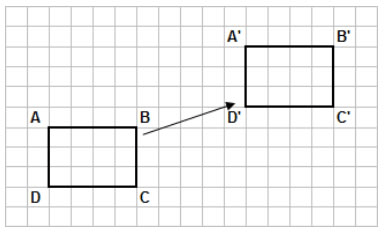
Translation, 1 unit up and 9 units right
100
True or False, when a dilation happens shapes are changing orientation or location but not size.
False, a dilation occurs when a shape is shrunk or enlarged.
100
What does it mean to be congruent?
Same shape and same size
100
True or False. When an image is dilated it changes size and shape.
False, a dilation will change size but the shape does not change.
100
What do we call the horizontal distance from one point to another?
Run
200
What transformation is happening in this image?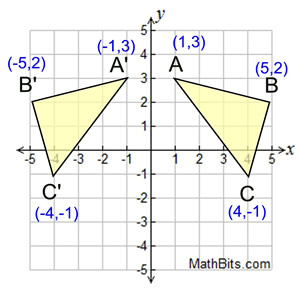 
Reflection, reflected over the y-axis
200
When performing a dilation can I multiply one side by 2 and the other by 3?
No, all sides need to change by the same scale factor.
200
What does it mean to be similar?
Same shape, different size
200
When a copy shape is larger than the original is the scale factor less than 1, equal to 1, or greater than 1?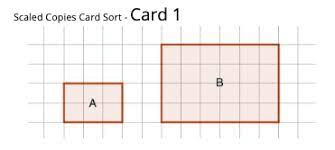 
Greater than 1, the sides are all increasing by the same scale factor
200
What do we call the vertical distance from one point to another?
Rise
300
What transformation is happening in this image?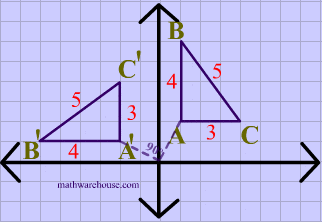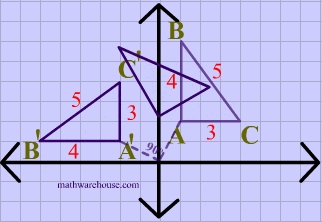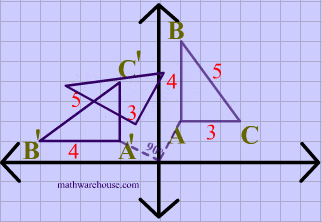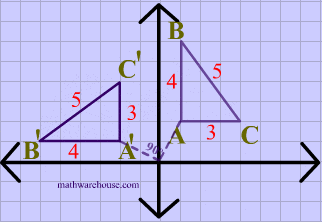 
Rotation, rotation 90 degrees counter clock wise around the origin.
300
Do these images show a dilation?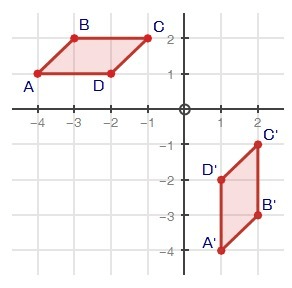 
No, the shape does not change size, just location.
300
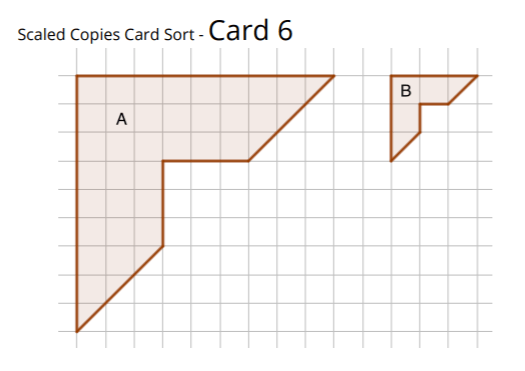
Are these shapes congruent?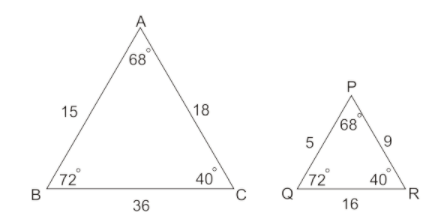 
No, the second one is smaller.
300
When a copy is smalled than the original shape is the scale factor less than 1, equal to 1, or greater than 1?
Less than 1, all the sides are getting smaller in the copy compared to the original.
300
When calculating slope we need to use a fraction. What do we put in the numerator and denominator? (rise or run)
Rise is in the numerator and run is in the denominator.
Rise/Run
400
What set of transformations occur to get from image 1 to 4? There are 2 steps.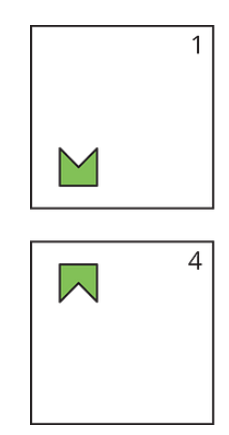 
1. Reflect up
2. Translate up
400
What transformation is needed to move from the original to the copy?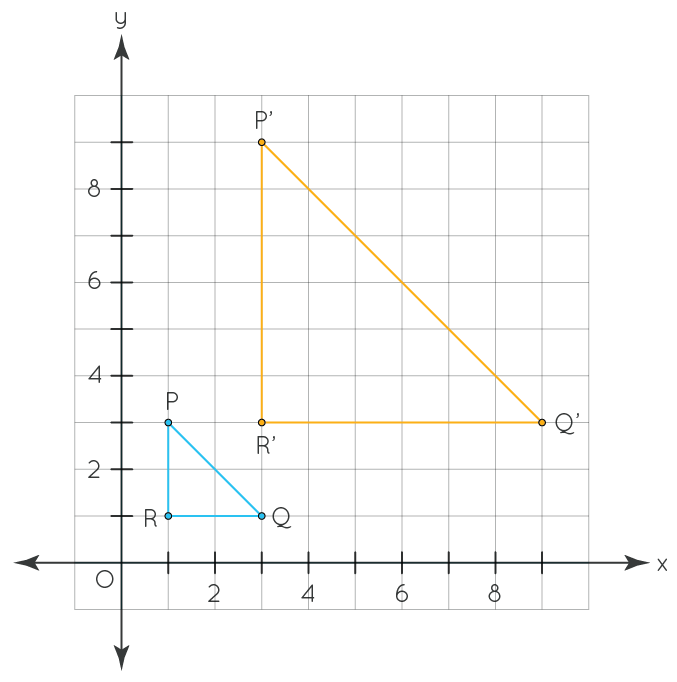 
Dilation, by a scale factor of 4 and a center at the origin.
400
Are these shapes similar?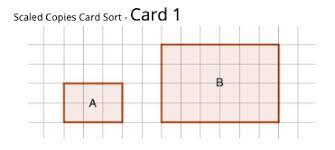 
Yes, they are both rectangles but the second one is just twice as big.
400
What is the scale factor if the shape stays the same size?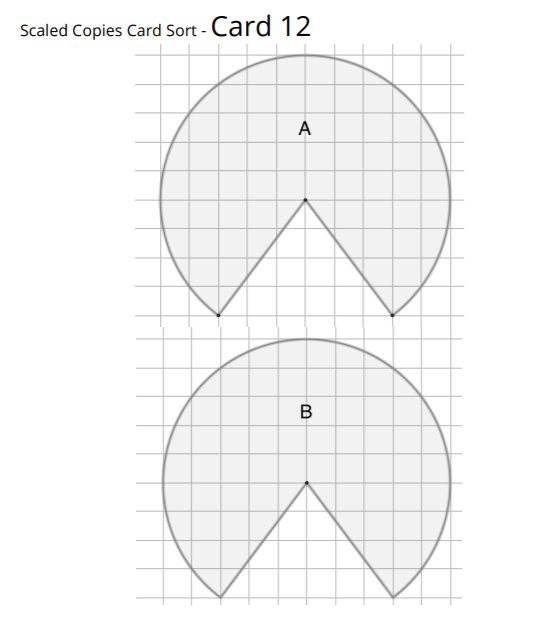 
1, all the sides are equal so they are being multiplied by 1 to stay the same.
400
What is the slope of this graph?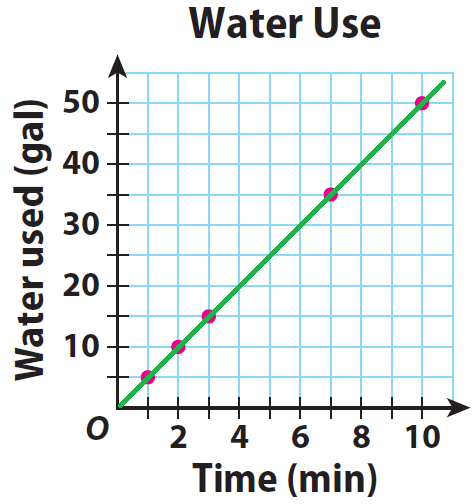 
5/1 or 5
500
Name the transformations that occur as we move from image 1 to image 6.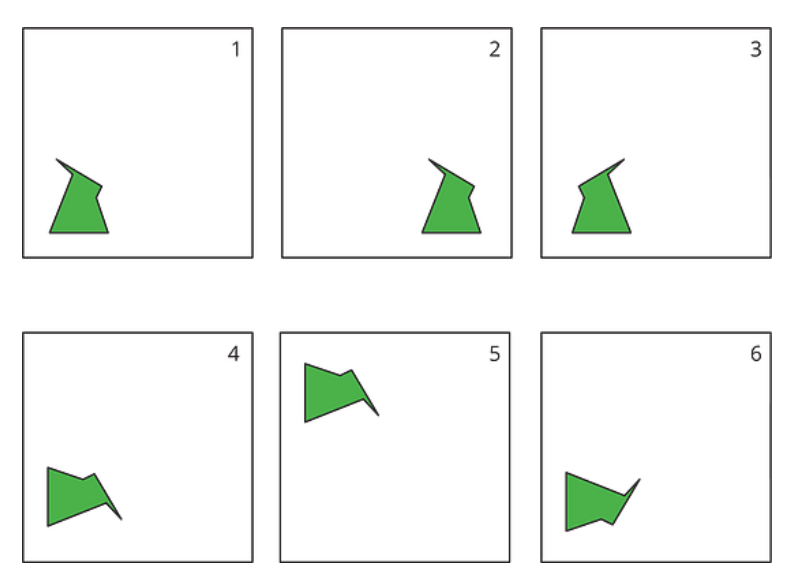 
1 to 2 translate right
2 to 3 reflect left
3 to 4 rotate 90 degrees clockwise
4 to 5 translate up
5 to 6 reflect down
500
What transformation is being shown in this image?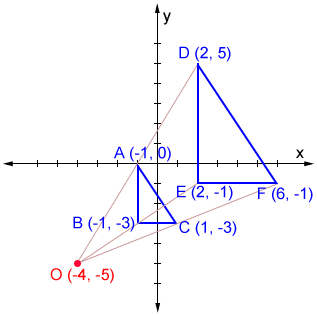 
Dilation, scale factor of 2 and a center at coordinate (-4, -5)
500
Are these shapes similar?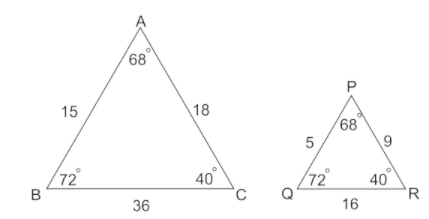 
No, the angles are the same but the sides do not have the same scale factor.
500
What is the scale factor of this dilation when starting with triangle ABC and moving to triangle DEF?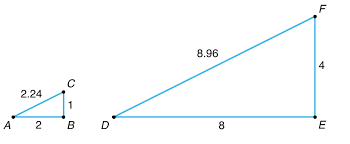 
4, each side is 4 times larger in the copy compared to the original.
500
Using these coordinates find the slope of the line that would connect these two points.
(2, 4) and (6, 20)
16/4 or 4/1 or 4