Identify the y-intercept.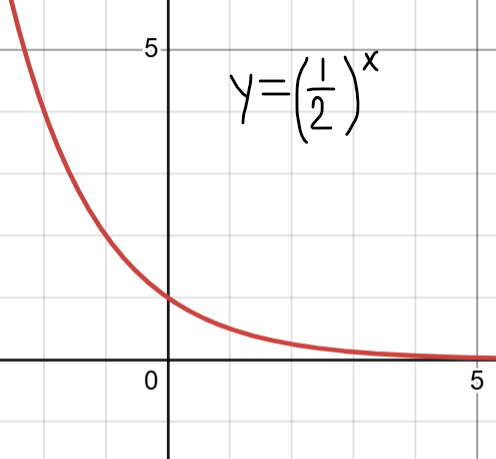
(0,1)
What is the growth factor for the function?
f(x)=3*2^x
2
(This means the y-values have a x2 pattern)
A computer valued at $6500 depreciates at the rate of 14% each year.
Write an exponential function to model the the value of the computer after t years.
A(t)=6500(1-0.14)^t
or
A(t)=6500(0.86)^t
Why does the function NOT have an x-intercept?
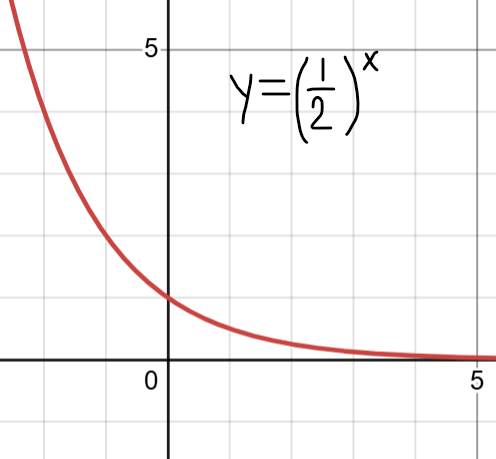
there is an asymptote on the x-axis (y=0) so the function never touches it!
How can we tell the function below represents decay without graphing?
f(x)=3*(1/2)^x
Because the factor is 1/2.
If you multiply by 1/2, the numbers will get smaller.
Find the amount of savings if $1,000 is deposited for three years at 8% annual interest, compounded annually.
$1,259.71
Where does the function have an asymptote?
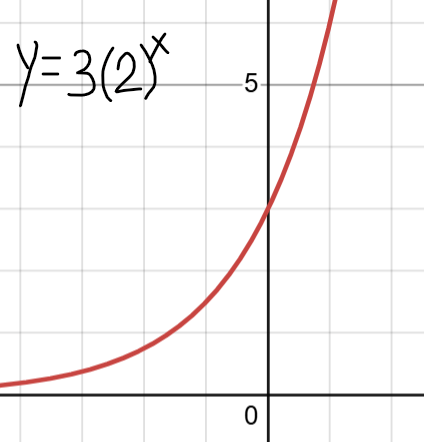
on the x-axis, y=0
Is the function exponential growth or decay?
f(x)=4*5^x
Growth
(x5)
At the end of one year, what would the total savings be on an initial deposit of $500 at 4% annual interest, compounded daily?
note: one year, in this case, is 365 days
$520.40
Identify the domain and range of the function.
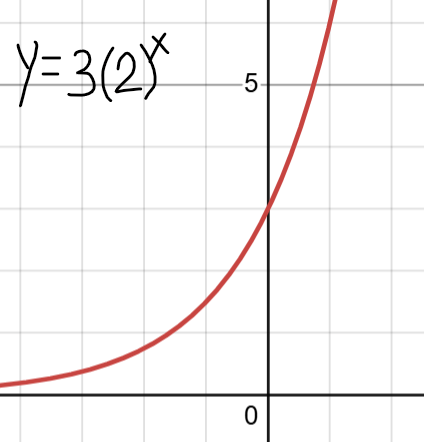
Domain:
(-oo,oo)
Range:
(0,oo)
Is the function exponential growth or decay? How do you know? (Think about what negative exponents do)
f(x)=3*5^-x
Decay!
A negative exponent will flip the 5 to 1/5
Find the total amount in the savings account at the end of two years, if the initial investment is $1,000 with an interest rate of 6%, compounded weekly.
$1,127.42
Identify the domain and range.
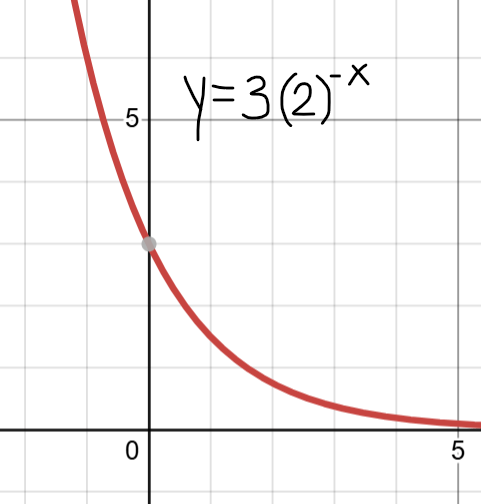
Domain:
(-oo,oo)
Range:
(0,oo)
Is the function exponential growth or decay? How do you know? (Think about what negative exponents do)
f(x)=2*(1/3)^-x
Growth!
the negative exponent will flip the 1/3 to 3/1 or 3
A computer valued at $6500 depreciates at the rate of 14% each year.
How many years will it take for the computer to worth less than $3000?
*Hint: Look at the graph!
A little over 5 years
(about 5.13)