Value Functions
Value Functions
Identify the vertex and slope of the following function.
y= |x-3|+4
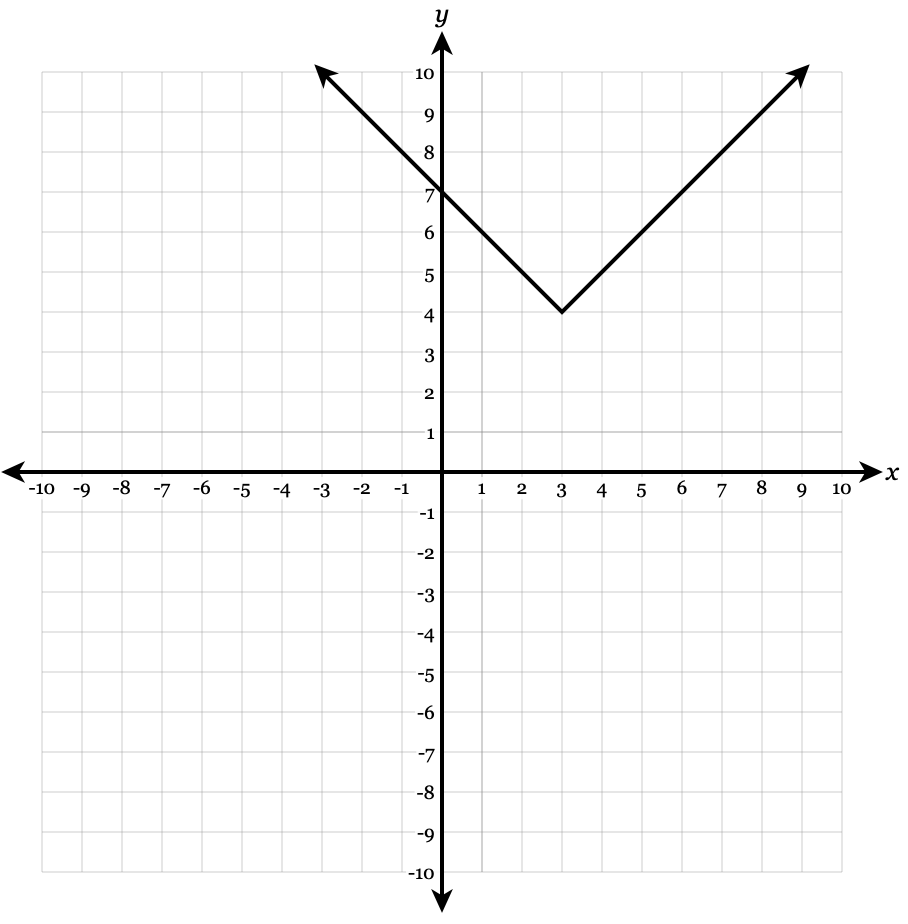
Vertex : (3,4). Slope: 1
Solve the absolute value equation ALGEBRAICALLY
-5|x-10|-15=0
-5 |x - 10| - 15 = 0
+ 15 +15
-5 | x - 10| = 15
(-5|x-10|)/-5= 15/-5
|x-10| = -3
No Solution
Solve the absolute value inequality by GRAPHING
|x-2|+3<7
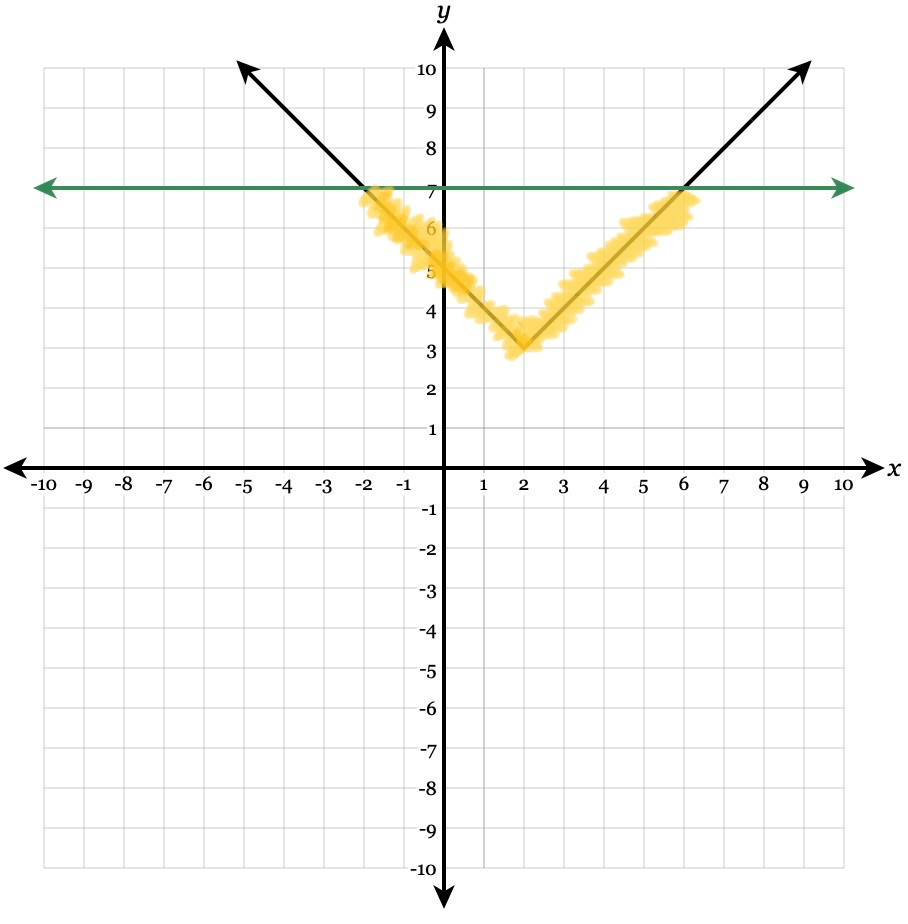 -2 < x< 6
-2 < x< 6
Identify all the transformations for the absolute value function.
y = |x| - 4
Translates down 4 units
Identify the vertex and slope of the following function.
y=-|x-4|+1
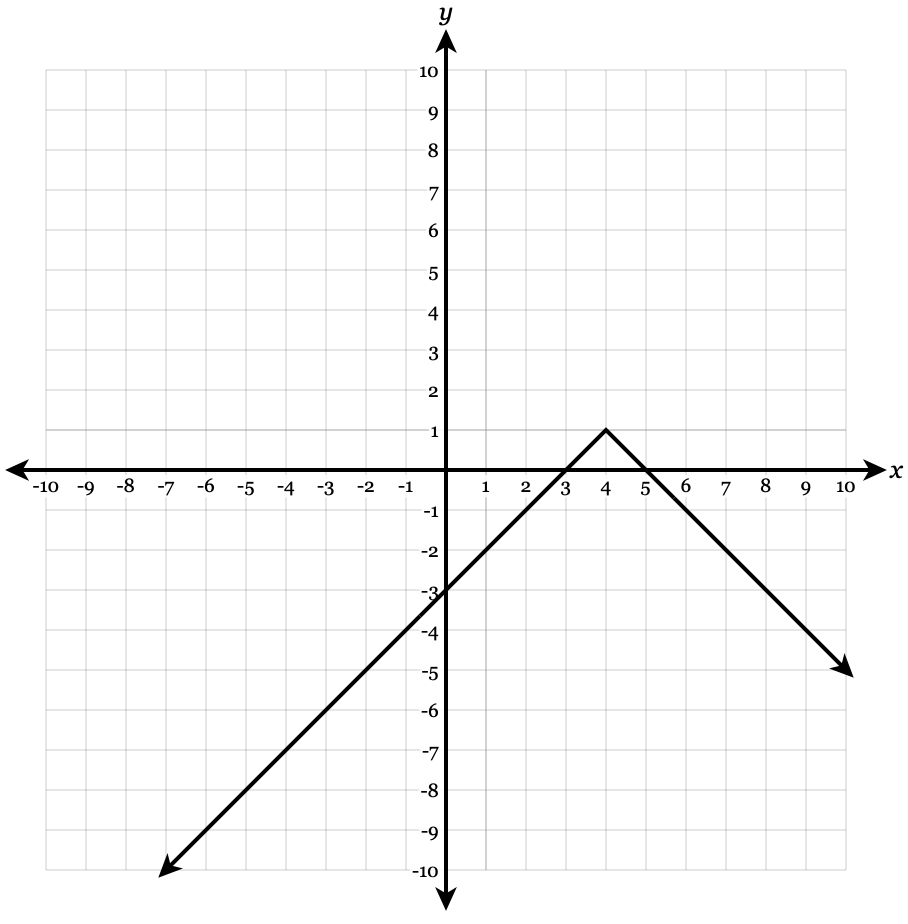
Vertex: (4,1). Slope: -1
Solve the absolute value equation by GRAPHING
|x+1|-4=1
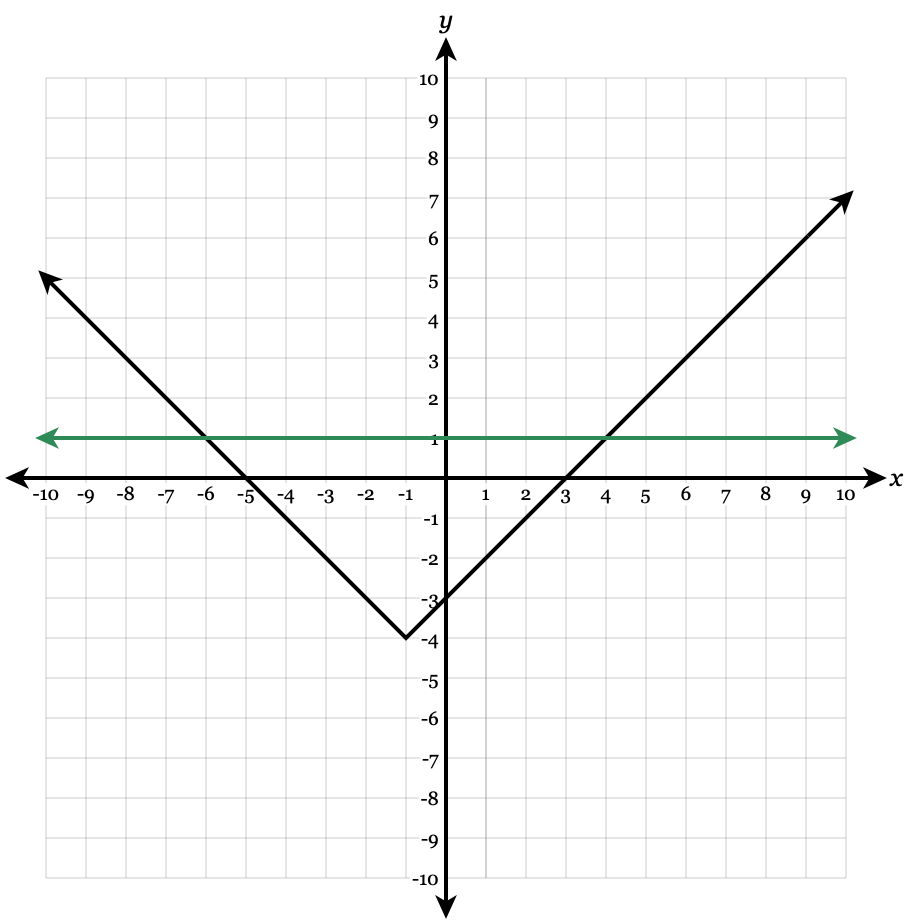
x=-6 and x=4
Solve the absolute value inequality ALGEBRAICALLY
|x+4|-22 > -18
|x + 4| - 22 > - 18
+ 22 + 22
|x + 4| > 4
x + 4 > 4 x + 4 < - 4
- 4 - 4 - 4 - 4
x > 0 or x < -8
Identify all the transformations for the absolute value function.
y = |x + 2| + 10
1. Translates left 2 units
2. Translates up 10 units
Identify the vertex and slope of the following function.
y=2|x+5|-3

Vertex: (-5,-3). Slope: 2
Solve the absolute value equation by GRAPHING
-3|x+3|+3=-3
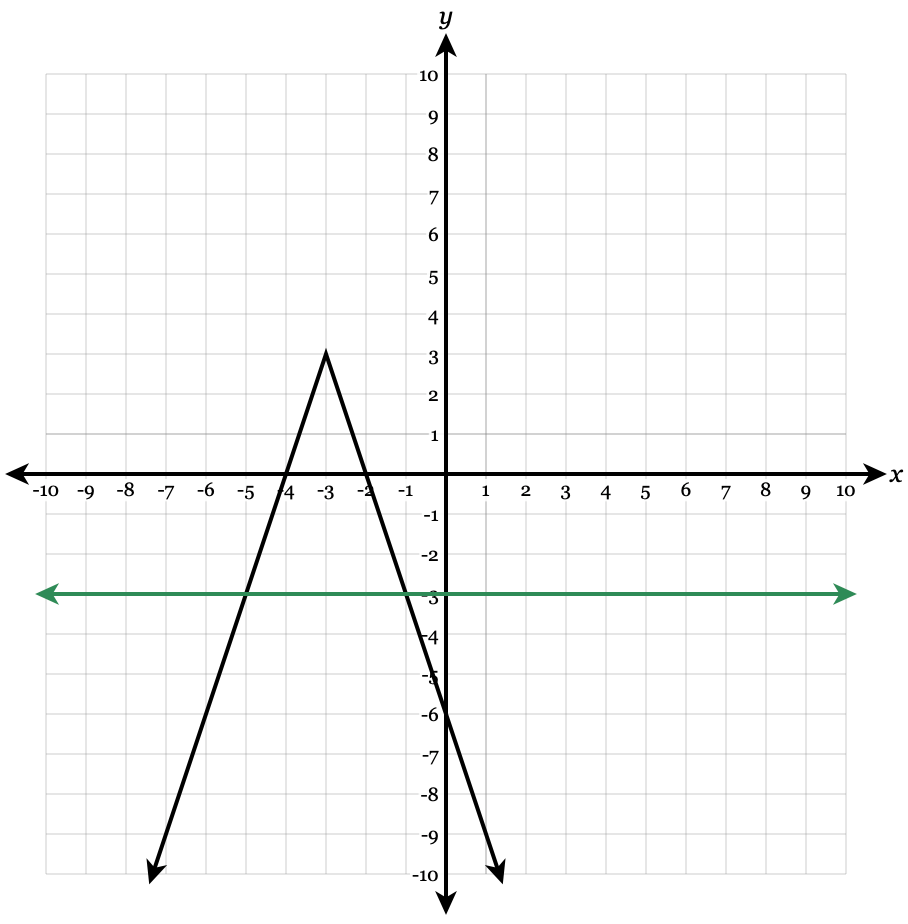
x = -5 and x = -1
Solve the absolute value inequality by GRAPHING
2|x+3|-3>=5
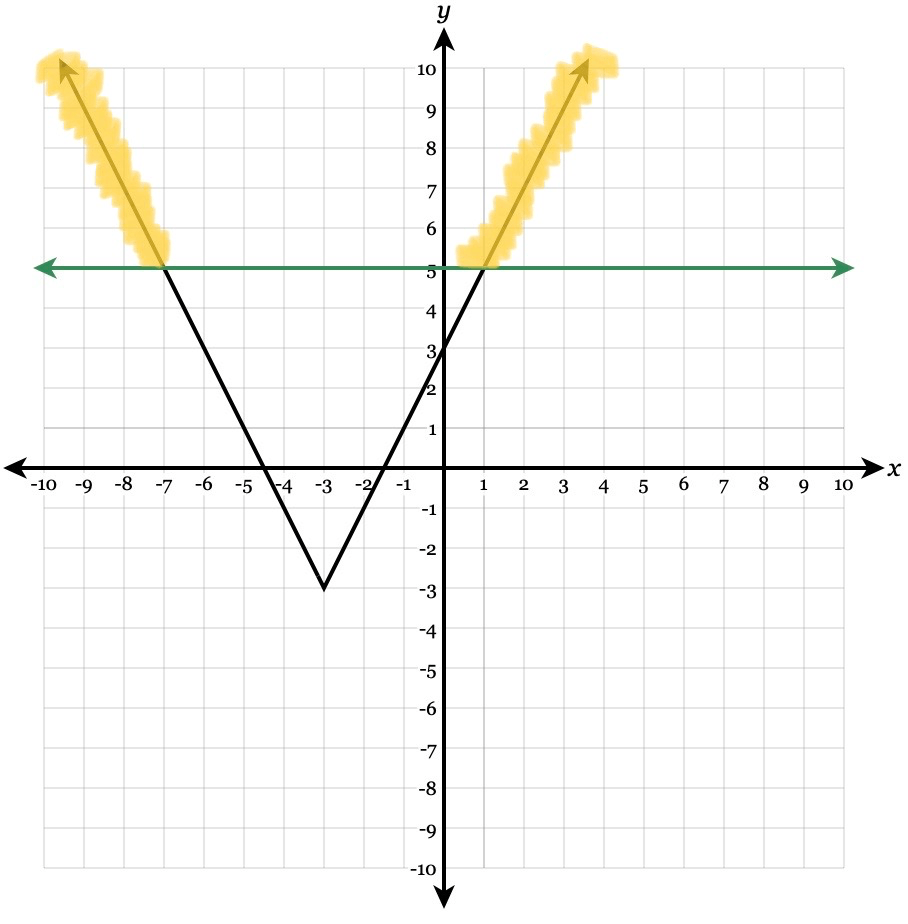
x <=-7 or x>=1
Identify all the transformations for the absolute value function.
y= - 1/2| x - 5| + 8
1. Reflects over x-axis
2. Vertical Compression by a factor of 1/2
3. Translates right 5 units
4. Translates up 8 units
Identify the vertex and slope of the following function.
y= 3|x+2|-5

Vertex: (-2,-5) Slope: 3
Solve the absolute value equation ALGEBRAICALLY
2|x-12|+5 = 15
2|x-12|+5 = 15
-5 -5
2|x-12| = 10
(2|x-12|)/2=10/2
x-12 = 5 x-12 = -5
+12 +12 +12 +12
x = 17 and x = 7
Solve the absolute value inequality ALGEBRAICALLY
5|7x-7|+8<=43
5|7x-7|+ 8 ≤ 43
- 8 - 8
5|7x-7|≤ 35
(5|7x-7|)/5 <= (35)/5
|7x-7| ≤ 7
7x - 7 ≤ 7 7x - 7 ≥ -7
+ 7 +7 + 7 +7
7x ≤ 14 7x ≥ 0
(7x)/7 <= 14/7 (7x)/7 >= (0)/2
x<= 2 x>= 0
0<= x <= 2
Identify all the transformations for the absolute value function.
y = 3 | -(x + 3)| - 2
1. Vertical stretch by a factor of 3
2. Reflects over y-axis
3. Translates left 3 units
4. Translates down 2 units
Identify the vertex and slope of the following function.
y=-2|x-2|+4
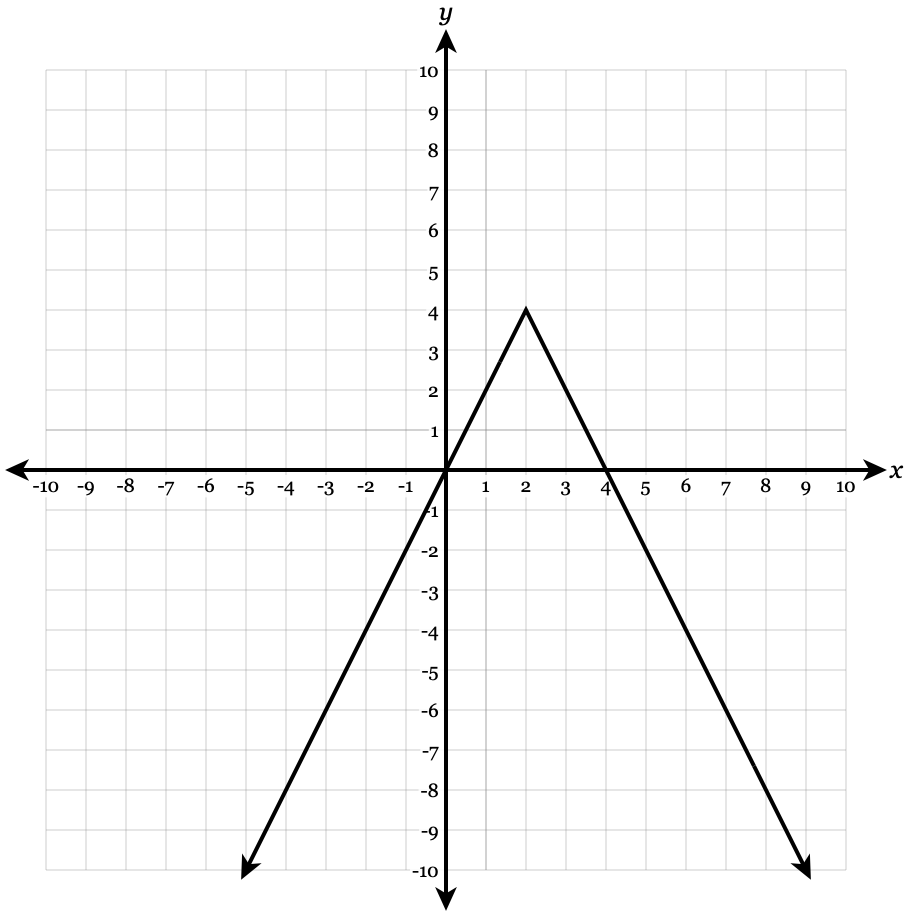
Vertex: (2,4). Slope: -2
Solve the absolute value equation ALGEBRAICALLY
4-5|10-5x|=-51
Work will be on the board
x=-1/5 and x= 21/5
Solve the absolute value inequality ALGEBRAICALLY
-3|1+2x|+2> -43
- 3 |1+2x|+ 2 > - 43
- 2 - 2
-3|1+2x| > - 45
(-3|1+2x|)/-3 < (-45)/-3
|1+2x| < 15
1 + 2x < 15 1 + 2x > -15
-1 -1 -1 -1
2x < 14 2x > -16
(2x)/2<14/2 (2x)/2 > (-16)/2
x<7 x> -8
-8<x<7
Identify all the transformations for the absolute value function.
y= -5|1/2(x+6)|-11
1. Reflects over x-axis
2. Vertical Stretch by a factor of 5
3. Horizontal Stretch by a factor of 2
4. Translates left 6 units
5. Translates down 11 units