Classify the polynomial by the degree and number of terms:
2x3
Degree of 3 - Cubic, Monomial
Add the Polynomials
(4x + 9) +(x - 4)
5x + 5
Subtract the polynomials:
(g - 4) - (3g - 6)
-2g + 2
Multiply the Polynomials:
3x2 (2x4)
6x6
The Pentagon building in Washington, D.C., is shaped like a regular pentagon. If the length of one side of the Pentagon is represented by n + 2, its perimeter would be represented by
What is 5n + 10.
Classify the polynomial by Degree and Number of Terms
5a2 - 6a
Degree of 2 - Quadratic, Binomial
Add the polynomials:
(-3a - 2) + (7a + 5)
4a + 3
Subtract the polynomials:
(-5h - 2) - (7h +6)
-12h - 8
Multiply the Polynomials:
(2x)(x + 2)
2x2 + 4x
The lengths of the sides of home plate in a baseball field are represented by the expressions in the accompanying figure.
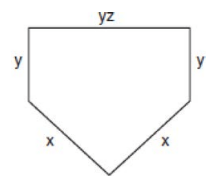 What is the expression that represents the perimeter of the figure?
What is the expression that represents the perimeter of the figure?
2x + 2y + yz
Classify the polynomial by Degree and Number of Terms
-6a4 + 10a3
Degree of 4 - Quartic, Binomial
Add the polynomials:
(x2 +3x + 5) + ( -x2 +6x)
9x + 5
Subtract the polynomials:
(-x2 - 5) - (-3x2 -x -8)
2x2 + x +3
Multiply the Polynomials:
(-3m)(-4m - 6)
12m2 + 18m
Express both the area of the rectangle shown in the accompanying diagram as a polynomial in simplest form.
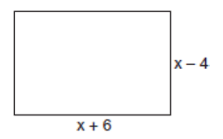
A = x2 + 2x − 24
Identify the coefficients in this polynomial
-10k3 + k +1
-10, 1
Add the polynomials:
(t2 + 3t3 -3) + (2t2 +7t -2t3)
t3 +3t2 +7t -3
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
Multiply the Polynomials:
(4n - 1)(5)
20n - 5
The perimeter of a square is 64 meters. Find the area of the square.
4 sides: 6
64/4=16
Each side is 16 meter. Therefore, the Area of the square is
16*16
which equals 256 m2
What is the degree of a constant?
Zero
Add the polynomials:
(-1 + x2 + 2x) + (1 -2x + 2x2)
3x2
Subtract the Polynomials:
(2x - 3x) - (x2 -2x + 4)
-x2 + x - 4
Multiply the Polynomials:
(6d)(d2 - 4d + 1)
6d3 - 24d2 +6d
A rectangular garden is going to be planted in a person’s rectangular backyard, as shown in the accompanying diagram. Some dimensions of the backyard and the width of the garden are given. Find the area of the garden to the nearest square foot.
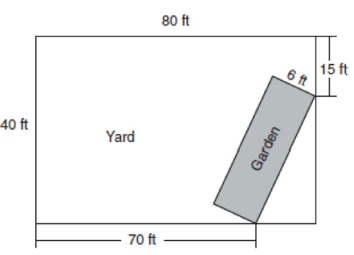
ANS: 162. The legs of the triangle formed by the garden in the corner of the rectangular backyard are 10 (80-70) feet and 25 (40-15) feet. Use Pythagoras to determine the length of the garden.
10^2+25^2=c^2
725=c^2
sqrt(725) =c
A=lw=6sqrt(725)~~ 162.