The value of y varies directly with x. If x=5, then y=45
Find the k, the constant of proportionality
k = 9
Find the slope of a line parallel to the given equation: y=−2x+10
slope = -2
Find the slope of a line perpendicular to the equatin
y = 3/4x+10
slope = -4/3
Describe how the function relates to the parent function
g(x) = f(x) +10
shifted 10 units up
f(x+c) will shift the line _____ "c" units
f(x-c) will shift the line _____ "c" units
left and right
The value of y varies directly with x. If x=5, then y=45
Write an equation to represent the situation
y=9x
Find the slope of a line parallel to the given equation: 2y=5x−10
Slope = 2.5
write the slope and the equation in slope-intercept form.
A line perpendicular to
y =5x +1 and contains the
point (0, 10).
y = -1/5x + 10
Describe how the function relates to the parent function
h(x) = f(x) –2
Shifted 2 units down
Describe how the functions given will relate to the parent function f(x) = x.
m(x) = f(x-5)
m(x) will be shifted 5 units to the right
The value of y varies directly with x. If x=6, then y=24
Find the value of x when y=48
x = 12
Find the slope of a line parallel to the given equation: 9y=12x+36
slope = 4/3
write the slope and the equation in slope-intercept form.
A line perpendicular to
y = 6x + 4 and contains the
point (12, -5).
y = -1/6x - 3
Describe the green function if its name is g(x)
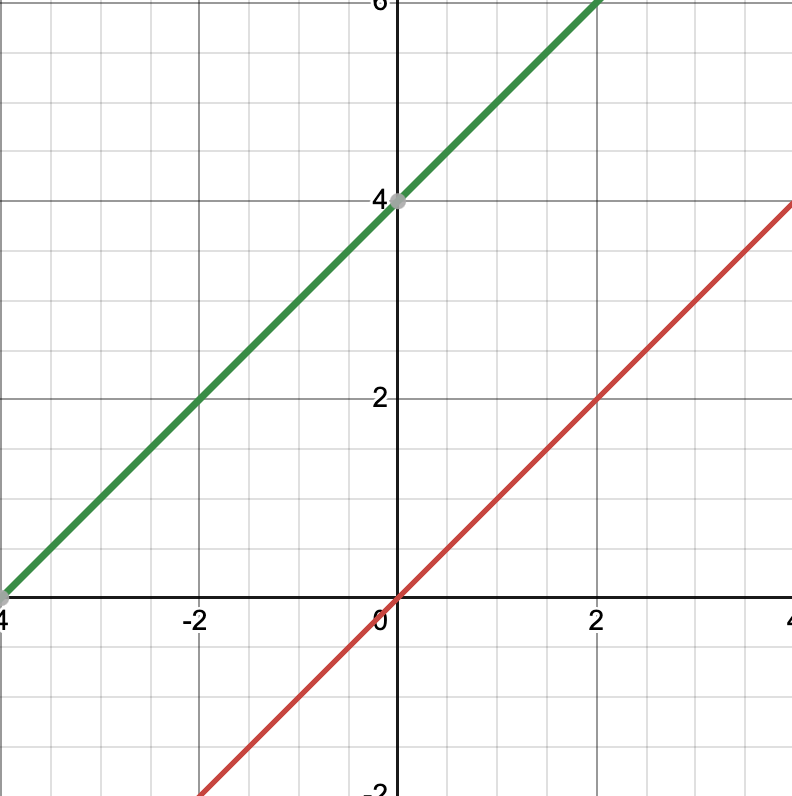
g(x) = f(x) +4
Describe how the functions given will relate to the parent function f(x) = x.
t(x) = f(x+22)
t(x) will be shifted 22 units to the left
The value of y varies directly with x. If x=8, then y=56
Find the value of y when x=14
y = 98
Write the equation of the line that is parallel to the line y=3x+5 and has a y-intercept of (0,2).
Slope: _______________
Equation: _______________
slope = 3
y int = 3
equation = y=3x+2
write the slope and the equation in slope-intercept form.
A line perpendicular to
y = -1/3x – 7 and contains the
point (-2, 7).
y = 3x + 13
If I transform the parent function vertically how do the slope change and how does the y intercept change?
Slopes remain the same
The y intercept changes by how much is added or subtracted to the function
Describe the green function in relation to the parent function if its name is h(x)
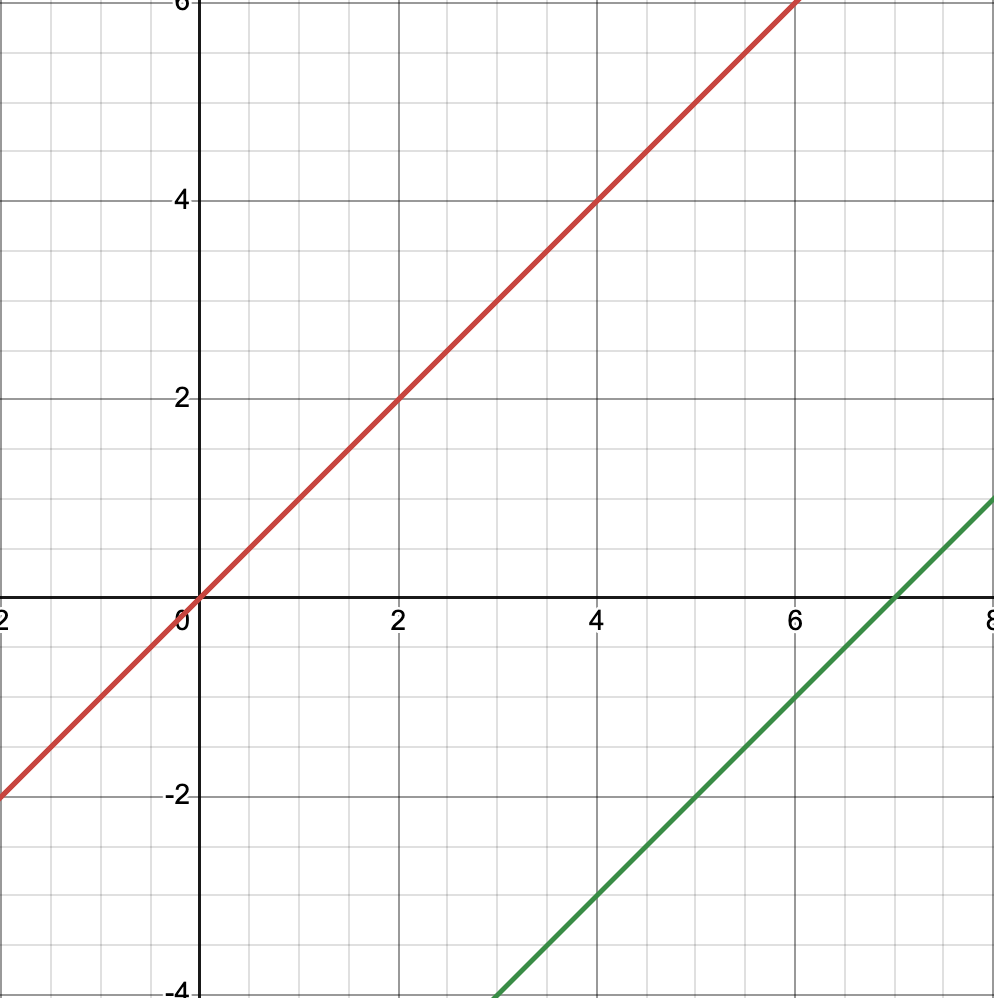
h(x) = f(x-7)
The cost of a frozen yogurt at Chill Treats is proportional to the number of ounces ordered. If a 12-oz serving costs $4.80, find the cost of a 15-oz serving
6 dollars
Write an equation in slope-intercept form. A line parallel to y=−25x+7 passes through the point (10,−2).
y = -25x +248
Write an equation for the line passing
through the point (-3,-5) that is
a. perpendicular to the x-axis
b.) perpendicular to the y-axis
a.) x = -3
b.) y = -5
The graph of f(x)= x2 is shifted up 5 units. Write the equation of the new function.
g(x) = f(x) +5
or g(x) = x2+5
The graph of f(x)=∣x∣ is shifted 3 units to the right.
- Write the equation of the new function.
- How does the vertex of the absolute value function change?
1.) h(x) = f(x-3)
2. ) the vertex moves 3 units to the right