What is the standard form of a quadratic equation, and what is the vertex form?
What makes two triangles SIMILAR?
The height, , in feet of an object above the ground is given by where t is the time in seconds. Find the time it takes the object to strike the ground and find the maximum height of the object. h 16 64 190, 2 h = − t + t + t ≥ 0
Which ratio corresponds to the tangent of angle A?

What is the COSINE law of angles
Find the solutions to the quadratic equation x2−13x+12=0
Show that the two triangles given in the figure below are similar.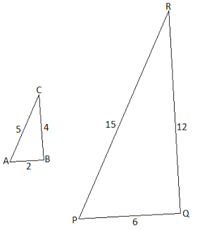
What is the height of the tree on the left?

Read more: https://www.mathwarehouse.com/trigonometry/sohcahtoa-real-world-applications.php#ixzz5aSX16ufH
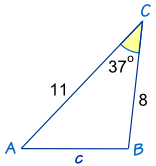
Find the length of side b if side c is 38 m and angle A is 48°

Work out angle m° in the diagram below:
Solve the quadratic equation x2+14x+45=0
Show that the two triangles given beside are similar and calculate the lengths of sides PQ and PR.
The angle of elevation from a point 43 feet from the base of a tree on level ground to the top of the tree is 30°. What is the height of the tree? Round your answer to the nearest tenth
Which ratio corresponds to cos35?

How long is side "c" ... ?
z^2−16z+61=2z−20
Find the length AB in the triangle shown beside.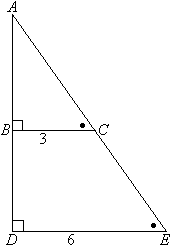
A 3 hour river cruise goes 15 km upstream and then back again. The river has a current of 2 km an hour. What is the boat's speed and how long was the upstream journey?

What is the value of sinθ?
A 4m flag pole is not standing up straight. There is a wire attached to the top of the pole and anchored in the ground. The wire is 4.17m long. The wire makes a 68° angle with the ground. What angle does the flag pole make with the wire?
09u^2−16=0
Trisha wants to measure the height of a building but she does not have the tools to do so. She noticed that there is a tree located in front of the building so she decided to use her smartness and the geometry knowledge that she got at school to measure the building height. She measured the distance between the tree and the building and found that it is 30m. She stood in front of the tree and started backing until she could see the top edge of the building from above the tree top. She marked her place and measured it from the tree. It was 5m.
Knowing that the tree height is 2.8m and Trisha’s eyes height is 1.6m, help Trisha to do the math and calculate the building height.
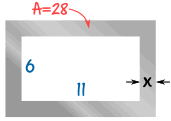
Your company is going to make frames as part of a new product they are launching.
The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm2
The inside of the frame has to be 11 cm by 6 cm
What should the width x of the metal be?
If the angle of elevation to the top of a tree is 65°. How far are you away from the tree, if the tree's height is 27 feet? Round your answer to the nearest tenth
Two scuba divers are 20m apart below the surface of the water. They both spot a shark that is below them. The angle of depression from diver 1 to the shark is 47° and the angle of depression from diver 2 to the shark is 40°. How far are each of the divers from the shark?
