Properties of Numbers
Solving Equations
Relations and Functions
Interpreting Graphs etc.
100
Name the property demonstrated:
3x + 0 = 3x
Additive Identity
100
Solve:
5k + 2 + 6÷2 = 3(k-1)
k = -4
100
Represent the relation as a graph, a table and a mapping. Determine if it is a function. State the domain and range.
{(1, 1), (2, 1), (3, 1), (4, 1)}
It is a function.
D:{1, 2, 3, 4}
R:{1}
100
Identify the independent and dependent variables:
The air pressure increases when you get to higher and higher altitudes.
independent: altitude
dependent:air pressure
200
Name the property demonstrated:
6 * 1/6 = 1
Multiplicative Inverse
200
Solve:
(5 + 8 ÷ 4) + 3k = 3(k +32) -89
All real numbers
200
Represent the relation as a graph, a table and a mapping. Determine if it is a function. State the domain and range.
{(1, 1), (1, 2), (1, 3), (1, 4)}
It is not a function because the input 1 has four different outputs.
D: {1}
R:{1, 2, 3, 4}
200
Identify the independent and dependent variables:
As you get closer and closer to the sun, the temperature increases.
independent: distance from the sun
dependent: temperature
300
Name the property demonstrated:
3 + 4 = 4 + 3
Commutative Property of Addition
300
Solve:
2(k+4) + 1 = 2k + 8^2 - 6*9
No solution
300
Represent the relation as a graph, a table and a mapping. Determine if it is a function. State the domain and range.
{(1,2), (2,3), (3,4), (4, 4)}
It is a function
D:{1,2,3,4}
R:{2,3,4}
300
Describe what is happening in the graph of a car's distance from home below:
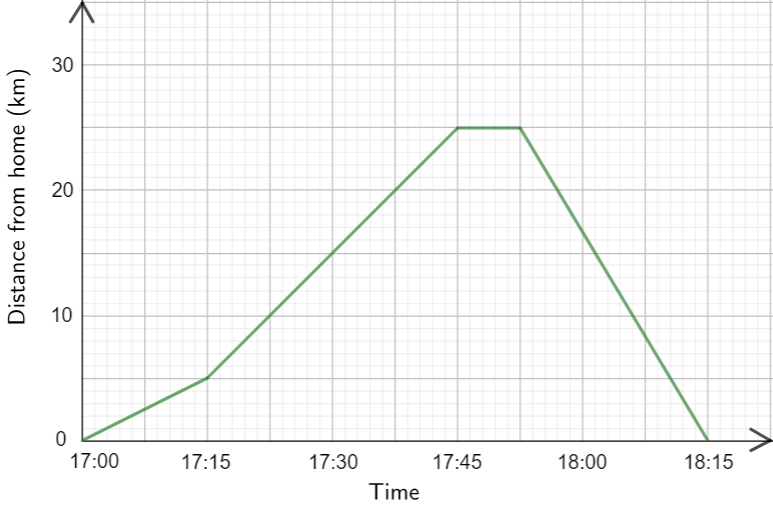
The car leaves home at 5 right at rush hour so they move pretty slowly but pick up speed. Then they arrive and stop for 7.5 minutes to pick up some takeout. Then they get back in the car and have a fast ride home now that traffic has died down.
400
Name the property demonstrated:
3 * (4 *2) = (3 *4) * 2
Associative Property of Multiplication
400
Solve:
3(b + 1) -5 = 3b -2
All real numbers
400
Represent the relation as a graph, a table and a mapping. Determine if it is a function. State the domain and range.
{(1,2), (2,3), (3,4), (3, 4)}
It is not a function.
D:{1, 2, 3}
R: {2,3,4}
400
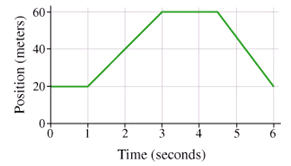Describe and interpret the graph using the intercepts, relative minima, relative maxima, where it is positive, where it is increasing, where it is decreasing, and the end behavior.
The y-intercept is at 20 m which means that is the position the person starts at. There is a relative minimum at 20 m which shows that is one of the closest positions and there is a relative maximum at 60 m which means that is one of the farthest positions. It is always positive which means the person is never going back past the starting point. It is increasing from 1 second to 3 seconds which means they are going further away and it is decreasing from 4 seconds to 6 seconds which means they are coming closer. The end behavior shows the person will keep coming closer.
500
Name the property demonstrated:
(x-5)*3 = 3x -15
Distributive Property
500
Solve:
4 + (3^2 + 7) ÷N = 8
N = 4
500
Represent the relation as a graph, a table and a mapping. Determine if it is a function. State the domain and range.
x =y^2
It is not a function because the input 4 has two different outputs, -2 and 2.
D:{ all numbers greater than 0}
R: {all real numbers}
500
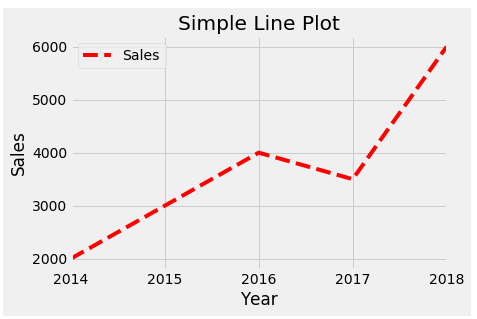Describe and interpret the graph using the intercepts, relative minima, relative maxima, where it is positive, where it is increasing, where it is decreasing, and the end behavior.
The y-intercept is at $2000 which shows that was how much money they started with in 2014. There was a relative maximum at 2016 which shows a peak in sales and a relative minimum at 2017 which shows a drop in sales. It is positive from 2014-2016 and 2017-2018 which shows sales are increasing and it is decreasing from 2016-2017 which shows sales are decreasing. The end behavior shows that sales will keep going up and up.