Parallel and Perpendicular
Inverse Functions
Equation of a Line
Line of Best Fit
100
Are the following two lines parallel, perpendicular, or neither?
3y -2x = 9
6x = -4y -5
Perpendicular
100
Find the inverse of the relation: {(2, 3), (4, -6), (-1 1), (-1, -1)}
{(3, 2), (-6, 4), (1, -1), (-1, -1)}
100
Write the equation of a line with slope 3/4 and y-intercept 3 in all 3 forms.
y - 3 = 3/4 (x - 0)
y = 3/4 x + 3
3x - 4y = -12
100
Determine whether the graph shows positive, negative, or no correlation. Describe its meaning if positive or negative.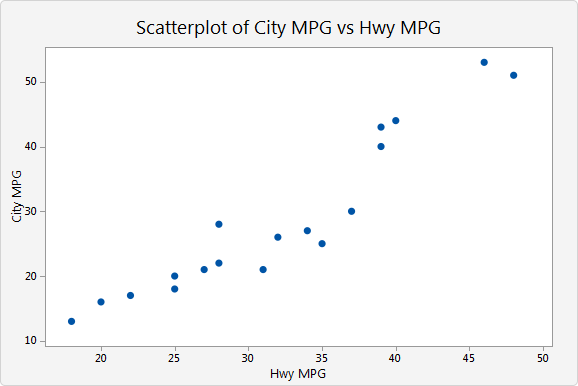 
Positive Correlation
As the Highway MPG increases, so does the City MPG
200
Find the equation of the line in point slope, slope intercept, and standard form that is parallel to the line 4y = 3x - 35 and goes through the point (2,5)
y - 5 = 3/4 (x -2)
y = 3/4 x + 7/2
3x - 4y = -14
200
Find the inverse of f(x) = -5x + 4 and graph both the lines.
f-1(x) = -1/5 x + 4/5
200
Write an equation in all three forms that passes through the points (-2, 5) and ( 8, -1)
y - 5 = 3(x + 2)
y = 3x + 11
3x - y = -11
200
Determine whether the graph shows positive, negative, or no correlation. Describe its meaning if positive or negative.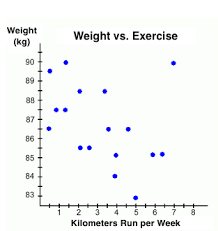
Negative Correlation
As you run more, your weight decreases.
300
Find the equation of the line in point slope, slope intercept, and standard form that is perpendicular to -3y + 5 = x that goes through the point (1,1).
y - 1= 3(x - 1)
y = 3x - 2
3x - y = 2
300
Find the inverse and graph both lines: 4x + 3y = 7
f-1(x) = -3/4 x + 7/4
300
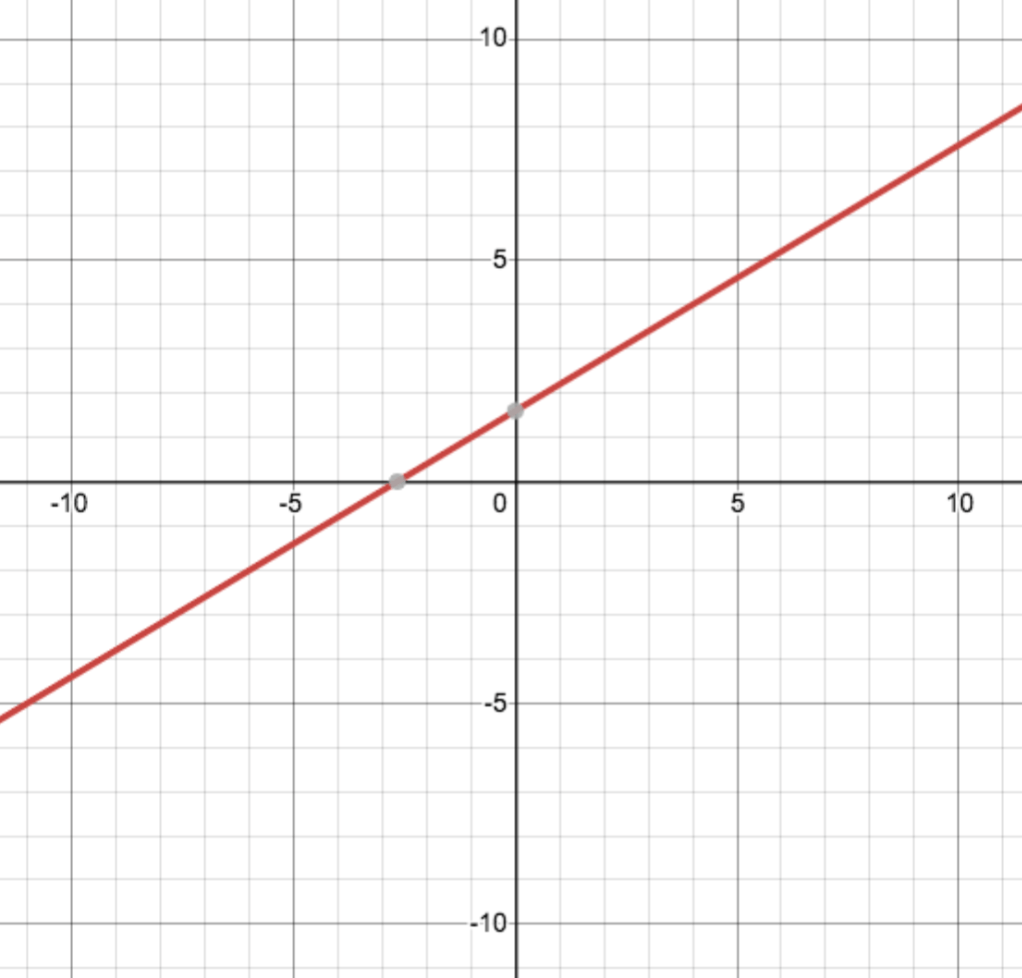
Graph the equation 5y - 3x = 8.
300
Create a line of best fit for the date using the points (20, 15) and (37, 30). Predict the City MPG for a car that gets 40MPG on the highway.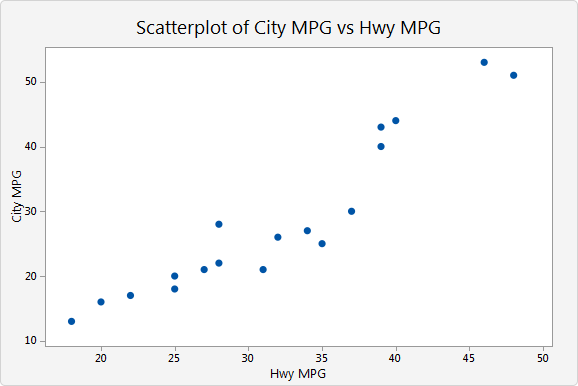 
y = 15/17x - 2.65
32.6 MPG
400
Find the equation of the line in point slope, slope intercept, and standard form going through the x-intercept and perpendicular to -7x = 7y + 2.
y - 0 = 1 (x + 2/7)
y = x + 2/7
x - y = -2/7
400
Jo pays $9 for every stuffed penguin she buys and $6 for shipping and handling.
a. Write an equation in function notation to represent the cost of Jo's order.
b. Find the inverse.
c. What do f-1(x) and x represent?
d. If Jo paid $141 for her order, how many penguins did she buy?
a. f(x) = 9x + 6
b. f-1(x) = 1/9 x - 2/3
c. x represents the total cost of the order and f-1(x) represents the number of penguins purchased
d. 15 penguins
400
The population of unicorns decreased at a constant rate of 12 unicorns per year. In the year 500 the population of unicorns was 5,000. Write an equation to represent the unicorn population in years after the year 400. Predict the population of unicorns in the year 600.
y = -12x + 6200
3,800 unicorns.
400
Create a line of best fit for the date using the points (2, 88.5) and (6, 85). Predict the kilometers run per week of someone weighing 50 kg.
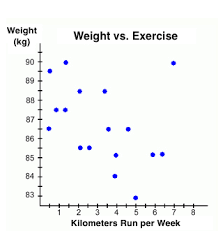
y = -7/8x+90.25
46 km
500
Are the following equations perpendicular, parallel, or neither?
-3x + 2y = 7
12x = 8y - 28
Neither, they are the same line.
500
If f(x) = 5x + a and f-1(10) = -1, find a.
a = 15
500
Write an equation in point slope for for the line that passes through the points (f,g) and (h, j).
y - g = (j-g)/(h-f) * (x -f)