How many solutions does the system have?
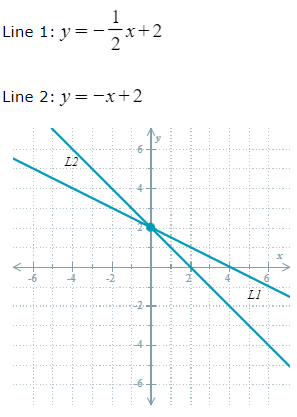
One solution: (0,2)
Multiply.
(4a-5)(6a+5)
24a2-10a-25
Solve.
(4v-6)(8-v)=0
v=3/2, 8
or
v=6/4,8 (non simplified)
A deli sandwich is placed inside a cooler. As the sandwich cools, its temperature C(t) in degrees Celsius after t minutes is given by the following exponential function.
C(t)=27(0.97)t
Find the initial temperature.
27 degrees Celsius
How many solutions does the system have?
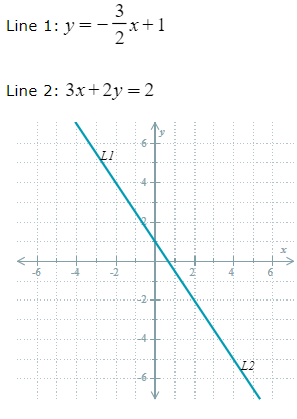
Infinitely many solutions
Solve the following system.
y - x = 15
x = 12
(12, 27)
Simplify.
(6v2+4)-(5v2-2v+1)
v2+2v+3
Solve the quadratic equation by graphing.
-x2+12x-27=0
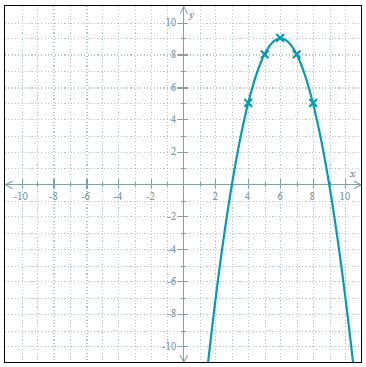
x=3,9
Suppose that the dollar value v(t) of a certain car that is t years old is given by the following exponential function.
v(t)=22800(1.12)t
Does the function represent growth or decay? Explain.
Growth, because b=1.12 is greater than 1
A deli sandwich is placed inside a cooler. As the sandwich cools, its temperature C(t) in degrees Celsius after t minutes is given by the following exponential function.
C(t)=27(0.97)t
By what percent does the temperature change each minute?
Decaying by 3%
Solve the following system.
y=6x
y=54
(9, 54)
Rewrite without parentheses.
-2v3(3v3-8v+6)
-6v6+16v4-12v3
x2-2x-15=0
x=-3,5
Suppose that the future price p(t) of a certain item is given by the following exponential function. In this function, p(t) is measured in dollars and t is the number of years from today.
p(t)=3200(1.025)t
By what percent does the price change each year?
Growth of 2.5%
Find the zeros of the quadratic function.
y=x2-16x+64
zero(s):8
or
x=8
Solve the following system of equations.
8x + 9y = 8
-3x + 5y = -3
(1, 0)
Rewrite without parentheses and simplify.
(6x-7)2
36x2-84x+49
Solve for y.
4y2-7y=2
x=-1/4,2
A laptop computer was purchased for $750. Each year since, the resale value has decreased by 23%.
Let t be the number of years since the purchase. Let y be the resale value of the laptop computer, in dollars.
Write an exponential function showing the relationship between y and t.
y=750(1-0.23)t
or
y=750(0.77)t
Use the quadratic formula to solve for x.
8x2-7x+1=0
x=0.70, 0.18 (rounded)
Exact answer below:
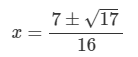
Solve the following system of equations.
-6x - 7y = -21
-3x - 8y = 3
(7, -3)
Factor completely.
3v2-24v+45
3(v-5)(v-3)
Also correct but not completely factored
(3v-15)(v-3)
(v-5)(3v-9)
Use the quadratic formula to solve for x.
3x2=3x+7
x=2.11, -1.11 (rounded)
Exact answer below: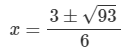
The table of ordered pairs (x,y) gives an exponential function.
Write an equation for the function.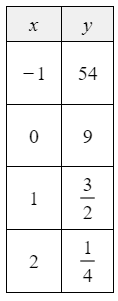
y=9(1/6)x
A principal of $2100 was invested at 3.75% interest, compounded annually.
Let t be the number of years since the start of the investment. Let y be the value of the investment, in dollars.
Write an exponential function showing the relationship between y and t.
y=2100(1+0.0375)t
or
y=2100(1.0375)t