Unit 6: Systems of Linear Equations
Unit 7: Polynomials
Unit 8: Quadratics
Unit 9: Exponential Functions
Unit 10: Statistics
100
How many solutions does the system have?
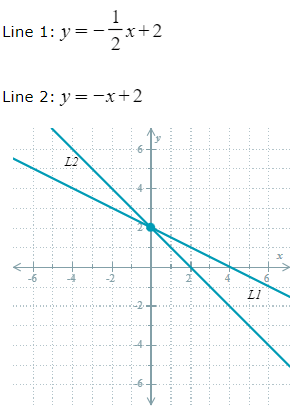
One solution: (0,2)
100
Multiply.
(4a-5)(6a+5)
24a2-10a-25
100
Solve.
(4v-6)(8-v)=0
v=3/2, 8
or
v=6/4,8 (non simplified)
100
A deli sandwich is placed inside a cooler. As the sandwich cools, its temperature C(t) in degrees Celsius after t minutes is given by the following exponential function.
C(t)=27(0.97)t
Find the initial temperature.
27 degrees Celsius
100
The noon temperatures (in Fahrenheit) for two cities were recorded over a given month.
Which city had the larger median noon temperature?
Infinitely many solutions
200
Solve the following system.
y = 8x
y = 2x+42
(7, 56)
200
Simplify.
(6v2+4)-(5v2-2v+1)
v2+2v+3
200
Solve the quadratic equation by graphing.
-x2+12x-27=0
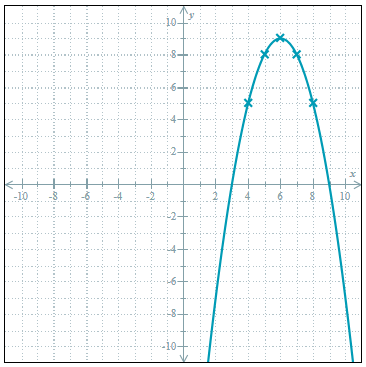
x=3,9
200
Suppose that the dollar value v(t) of a certain car that is t years old is given by the following exponential function.
v(t)=22800(0.82)t
Find the growth or decay rate.
Decay 18%
200
A deli sandwich is placed inside a cooler. As the sandwich cools, its temperature C(t) in degrees Celsius after t minutes is given by the following exponential function.
C(t)=27(0.97)t
By what percent does the temperature change each minute?
Decaying by 3%
300
Solve the following system.
y=4x+6
y=6x-8
(7, 34)
300
Rewrite without parentheses.
-2v3(3v3-8v+6)
-6v6+16v4-12v3
300
Solve for x.
x2-2x-15=0
x=-3,5
300
Suppose that the future price p(t) of a certain item is given by the following exponential function. In this function, p(t) is measured in dollars and t is the number of years from today.
p(t)=3200(1.025)t
Find the growth or decay rate.
Growth of 2.5%
300
Find the zeros of the quadratic function.
y=x2-16x+64
zero(s):8
or
x=8
400
Solve the following system of equations.
-3x + 8y = 12
5x - 3y = -20
(-4, 0)
400
Rewrite without parentheses and simplify.
(6x-7)2
36x2-84x+49
400
Solve for y.
4y2-7y=2
x=-1/4,2
400
A laptop computer was purchased for $750. Each year since, the resale value has decreased by 23%.
Let t be the number of years since the purchase. Let y be the resale value of the laptop computer, in dollars.
Write an exponential function showing the relationship between y and t.
y=750(1-0.23)t
or
y=750(0.77)t
400
Use the quadratic formula to solve for x.
8x2-7x+1=0
x=0.70, 0.18 (rounded)
Exact answer below:
500
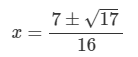
Solve the following system of equations.
-6x - 7y = -21
-3x - 8y = 3
(7, -3)
500
Factor completely.
5p2-p-18
(5p+9)(p-2)
500
Use the quadratic formula to solve for x.
3x2=3x+7
x=2.11, -1.11 (rounded)
Exact answer below: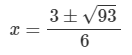
500
The table of ordered pairs (x,y) gives an exponential function.
Write an equation for the function.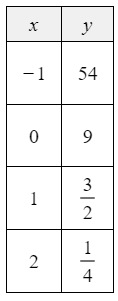
y=9(1/6)x
500
The 8 students in Mrs. Adams' class were asked how many minutes it takes them to get to school in the morning. Here is what they answered.
4, 5, 13, 9, 15, 12, 14, 12
Find the mean and median travel times. (round to the nearest tenth)
Mean = 84/8 = 10.5
Median = 12