Function Basics
Sequences
Slope
Equations of Lines
Systems of Equations
100
Finish the Definition:
"A function is:..."
...a relationship that maps exactly one x to one y
100
The next three terms in the sequence 3,7,11,...
...15,19,23
100
The definition of the slope of a line
What is the rise over run
or "change in y divided by change in x"
100
An equation of a line in slope-intercept form is
y = mx+b
The b stands for _________
The y-intercept
100
A system of equations is
Two or more equations in two or more variables
200
All possible x values (inputs)
Domain of a function
200
In the function an = a1 + (n-1)d, "d" refers to this
The common difference
200
Given the points (3,2) and (9,7) the slope is
5/6
200
Write the equation, in slope-intercept form,
of the line with slope -3 and y-intercept 7
y = -3x + 7
200
The solution to a system of equations
An ordered pair (x,y) that satisfies all equations in the system.
OR
The point at which all lines in the system intersect
300
Data that contains all values on an interval
Continuous
300
In the formula an = a1 + (n-1)d, a1 is this
The first term in the sequence
300
Calculate the rate of change from the following table
x 0 1 2 5 7
y -2 0 2 8 12
m = 2
300
The form of the line that looks like
y - y1 = m(x - x1)
Point-slope form
300
Is the point (1,8) a solution to the system
y = 3x + 5
y = -2x + 4
NO
400
The graph is that of a function (True or False?)
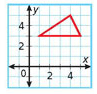
FALSE
- a function will pass the vertical line test
400
Identify a1 and d in the following sequence:
4, 15, 26, 37, ...
4
d = 11
400
Draw a line with a slope of zero
____________________
400
Write the equation of a line parallel to y = -0.5x - 12
that goes through (-2,8) in slope-intercept form
y = -0.5x + 7
400
Solve the following system by graphing:
y = x - 3
y = -x -1
NOTE: Solution is a point
(1, -2)
500
Mark has already sold $20 in tickets for the school play. He has four tickets left to sell at $2.50 per ticket. Write a function to describe how much money Mark can collect from selling tickets.
f(x) = 2.50x + 20
or
f(x) = 20 + 2.50x
500
Given the sequence -22, -31, -40, -49, ...
Write the function to find the nth term, then calculate the 81st term.
an = -22 -9(n-1)
a80 = -742
500
The lines whose slopes are -4 and 1/4 are
Perpendicular
500
Using the data from the table, draw a line of best fit for the scatterplot:
x 0 1 2 2 3 4 5 5 6
y 2 3 5 4 6 6 7 8 9
Teacher will choose the best line of fit
500
Solve the system by substitution
2x + y = 5
y = x - 4
NOTE: The solution is a point
(3, -1)