(Non Proportional)
Decreasing Functions
Which of the following patterns will create a linear function.
+5
-3
xx12
+5
-3
What is the difference between a proportional function and a non-proportional function?
Proportional passes through the origin. Non-proportional does not pass through the origin
What type(s) of pattern happens for an exponential function?
Multiplication or Division
Write a recursive formula for the sequence below.
13, 15, 17, 19
Explicit Formula:
a(n)=2n+11
Recursive formula:
f(1)=13
f(n+1)=f(n)+2
n>=1
What time interval is the function decreasing?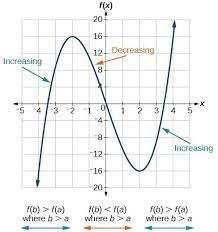
You are sell burgers to customers according to the following table. Write the equation that gives the number of burgers sold, y, as a linear function of the time (in hours) you sell the burgers, x.
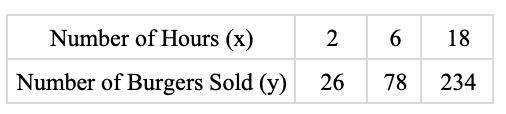
y=13x
A car rental company charges a one-time fee plus an amount per day. What is the initial value on the graph? What is the rate of change?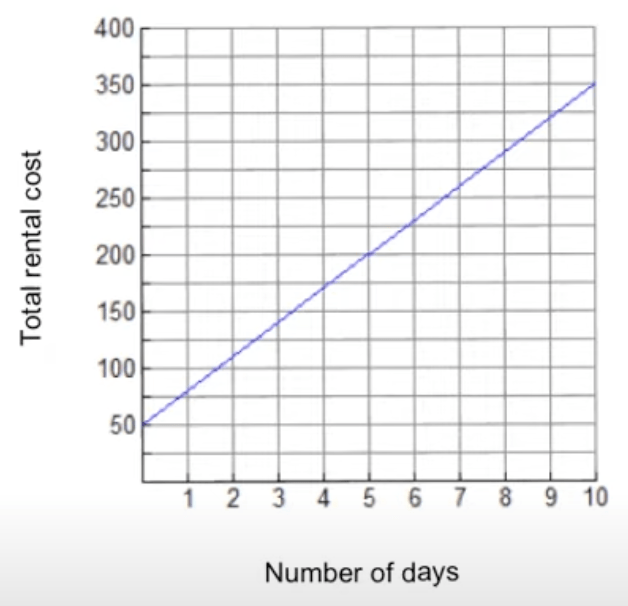
Initial Value - $50
Amount per day:
m=(/_\y)/ (/_\x)=(200-50)/(5-0)=150/5=30
$30 per day
Which of the following scenarios represent an exponential function? More than one may apply.
A. Hourly pay rate of $23.
B. Bacterial populations tripling every 12 hours.
C. Tax rate of 7.5%.
D. Driving down the highway at 65 miles per hour.
B and C only.
The other two are linear.
Write an explicit formula for the following sequence:
3, 9, 27, 81
Explicit Formula:
a(n)=3(3)^(n-1)
Recursive formula:
f(1)=3
f(n+1)=3f(n)
n>=1
What time interval is the function increasing?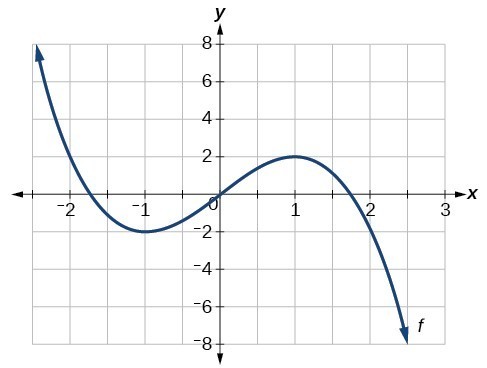
(-1,1)
Miki Sudo holds the women's word record for eating 48.5 hot dogs in 10 minutes. If she at them at a constant rate, write a linear equation representing the situation.
y=4.85x
rate = m = 48.5/10
An online DVD rental site charges a monthly membership fee of $10, plus $4 per DVD that is rented. The relationship between the number of DVDs rented and the total charge per month can be expressed with the equation y = 4x + 10, where x is the number of DVDs rented and y is the total charge per month. Find the domain and range of this relationship.
In this example, the independent variable, x, is the number of DVDs rented. The possible x-values include all whole numbers, since only whole number of DVDs can be rented.
The dependent variable, y, is the total charge per month. The possible y-values include 10, 14, 18, 22, . . .
Therefore, the domain is {0,1,2,3, . . .}, and the range is {10,14,18, 22, . . .}.
The National Association of Realtors estimates that, on average, the price of a house doubles every 10 years. Tony's grandparents bought a house in 1960 for $10,000. What was the value of Tony's grandparents house in 1970? 1980?
What is the equation that represents this situation?
1960 - $20,000
1970 - $40,000
h(t)=10000(2)^t
Write an explicit formula for the following sequence:
5, 1, -3, -7
Explicit Formula:
a(n)=-4(n-1)+5
a(n)=-4n+9
Recursive formula:
f(1)=5
f(n+1)=f(n)-4
n>=1
What time interval is the function increasing? Decreasing?
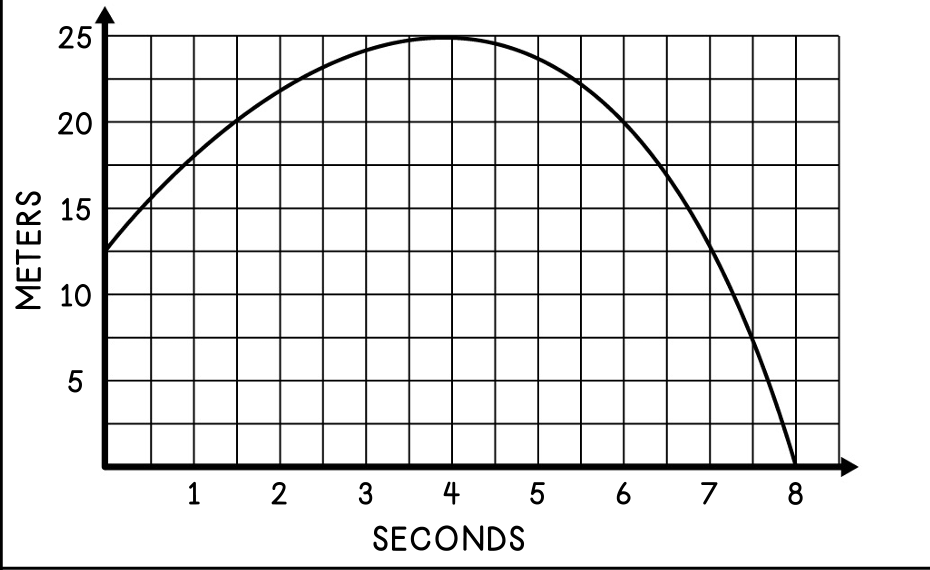
Increasing from 0-4 seconds.
Decreasing from 4-8 seconds
A clown at a birthday party can blow up five balloons per minute. The relationship between the number of balloons inflated and the time that has passed can be expressed with the equation y = 5x, where x is the number of minutes passed and y is the number of balloons inflated. Find the domain and range of the relations. 
Therefore, the domain is {x ≥ 0}, and the range is {y ≥ 0}.
Janelle and Matt run their own tutoring business's. Janelle charges an initial fee of $75 and then, $10 per hour of tutoring. Matt charges an initial fee of $50 and then $20 per hour of tutoring. Write equations for both businesses and determine when they will charge the same amount
J(t)=75+10t
M(t)=50+20t
When will 75+10t=50+20t?
2.5 hours.
In 2002, there were 450 households in the city of Klean that recycled. Each year since 2002, the number of households that recycle has grown by 8%. Write a function to represent the number of households in Klean that recycle t years since 2002. How many households recycle in 2012? Round to the nearest whole number (can't have 1/2 a person)
R(t)=450(1.08)^t
In 2012, t=10.
R(10)=972 households
Write an explicit formula for the following sequence:
100, 10, 1, 0.1, 0.01, ...
Explicit Formula:
a(n)=100(1/10)^(n-1)
Recursive formula:
f(1)=100
f(n+1)=f(n)/10
n>=1
Which of the following functions is increasing? How do you know?
A.
f(t)=3(1.2)^t
B.
g(t)=3(0.8)^t
A is increasing because the rate is greater than 1.