(12 - 15i) + (6 - 9i)
(18 - 24i)
Solve for x
x^2 = -144
x = 12i or - 12i
(4x^3- 2x + 1) + (7x^2 + 12x)
4x^3 + 7x^2 + 10x + 1
What are the degree, leading coefficient, and constant term of this polynomial:
5x^3 - 9x^5 + 6
Degree: 5
LC: -9
Constant: 6
Does this model represent exponential growth or decay?
y = 312 * (1 - 0.06)^t
Decay
Convert to logarithmic form:
7^3 = 343
log_7(343) = 3
8i(7 - 4i)
32 + 56i
Solve for x
-5x^2 + 2 = 17
x = sqrt3 i or -sqrt3 i
3x^2(5x^2 + x + 4)
15x^4 + 3x^3 + 12x^2
Sketch the end behavior of this polynomial:
-7x^5 + 4x^3 - 9x^2
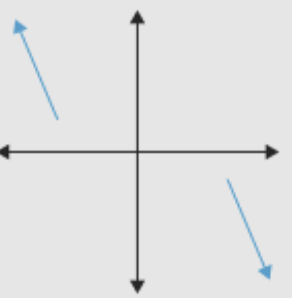
Write an exponential model for this scenario:
Amari deposits $6000 in a bank account with 2.3% yearly interest, deposited incrementally. Show the balance after t years have passed.
f(x) = 6000*(1.023)^t
Convert to exponential form:
log(800) = 2.9030
10^2.9030 = 800
(4 + 11i) - (-3 + 6i)
7 + 5i
Solve for x:
4x^2 + 2x + 5 = 0
x = \frac(-2 +- sqrt76 i)(8)
(-10x^6 + 7x^2 - 8) - (4x^6 - 3x^2 + 2x)
-14x^6 + 10x^2 - 2x - 8
What are the zeroes of the polynomial
(x - 4)(2x + 1)(x - 9)^2
x = 4, -1/2 , 9
The value of a 3D printer depreciates by 5% each month after its purchase. If it was bought for $1050, what will it sell for after a year and a half?
$417.08
Solve for x:
e^(4x) = 50
x = ln(50)/4. or 0.978
(6 - 2i)(-4 + 10i)
-4 + 68i
Solve for x:
-x^2 + 7x - 12 = 3
x = \frac(-7 +- sqrt11 i)(2)
(4x^5 - 3x^4 + 2x)(-x^3 + 5x^2)
-4x^8 + 23x^7 -15x^6 - 2x^4 + 10x^3
Which graph could match the equation
-54x^5-30x^3 - 1
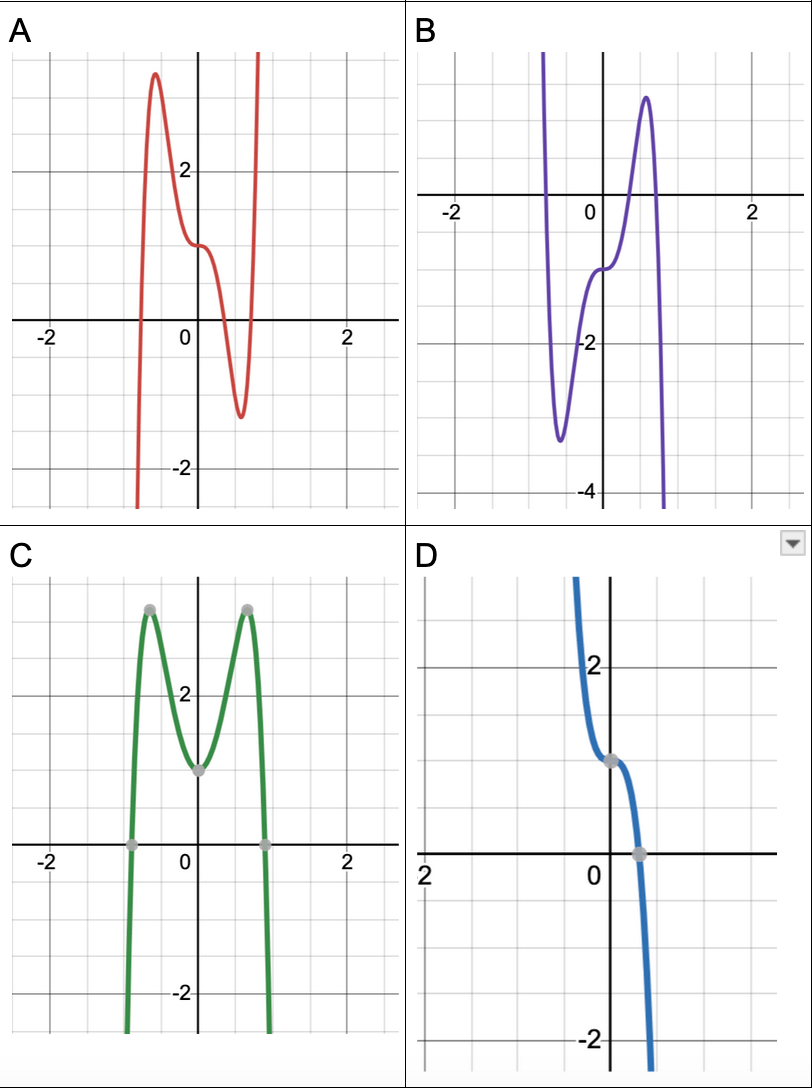
Graph B
The population of rabbits in a forest after t years is given by the function:
f(x) = 40*(3.5)^t
What is the daily growth rate of the population?
3.5^(1/365) = 1.003
1.003
The number of infected cells in a disease control experiment after t hours is given by the function.
c(t) = 500e^(-0.045t)
When will the number of cells fall to 200?
t = 20.36 hours
(3 + 2i)(1 - 4i) + 10i
11
Solve for x:
3x^2 - 5x + 6 = 2
x = \frac(5 +- sqrt47 i)(6)
(3x + 1)(2 - 9x^2) - (4x^3 + 8x^2 - x)
-31x^3-17x^2+7x+2
The degree is: even / odd
The leading coefficient is: positive / negative
The constant term is:
The zeroes are:
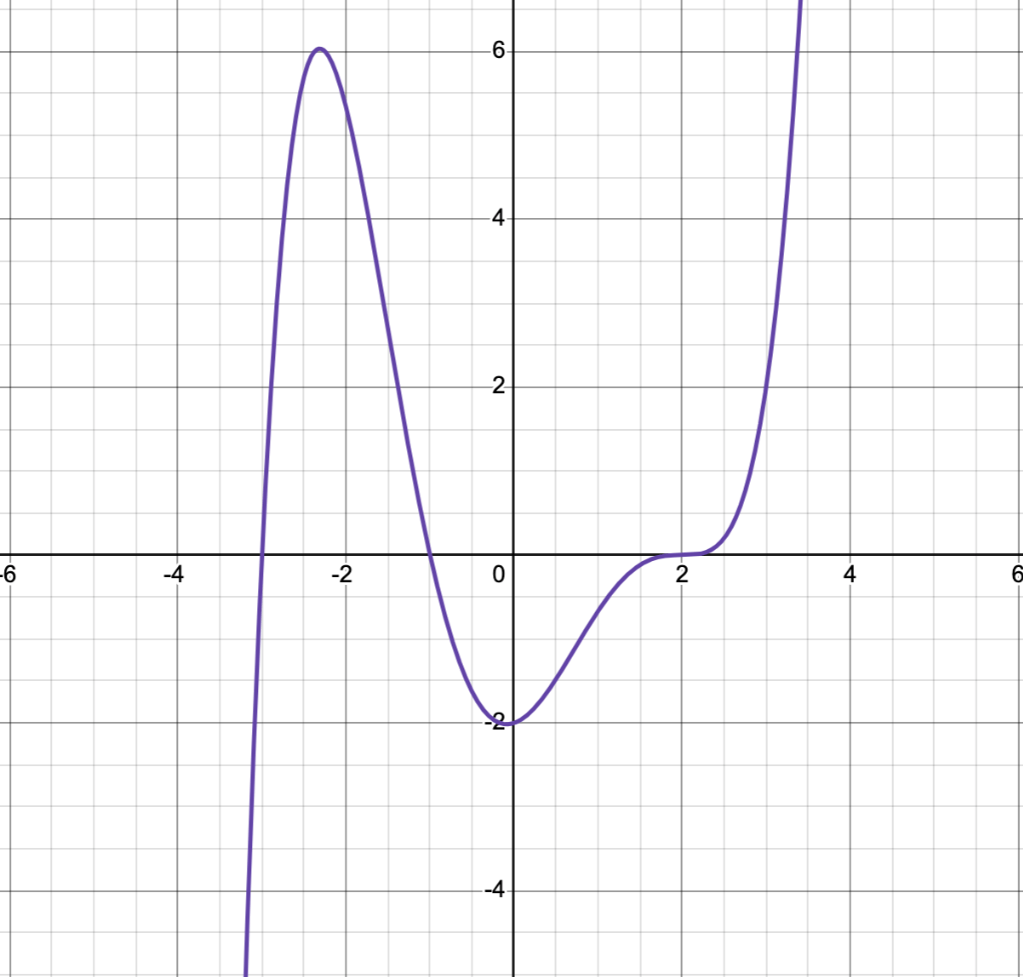
The degree is: odd
The leading coefficient is: positive
The constant term is: -2
The zeroes are: -3, -1, 2
Write the exponential function that would create this graph:
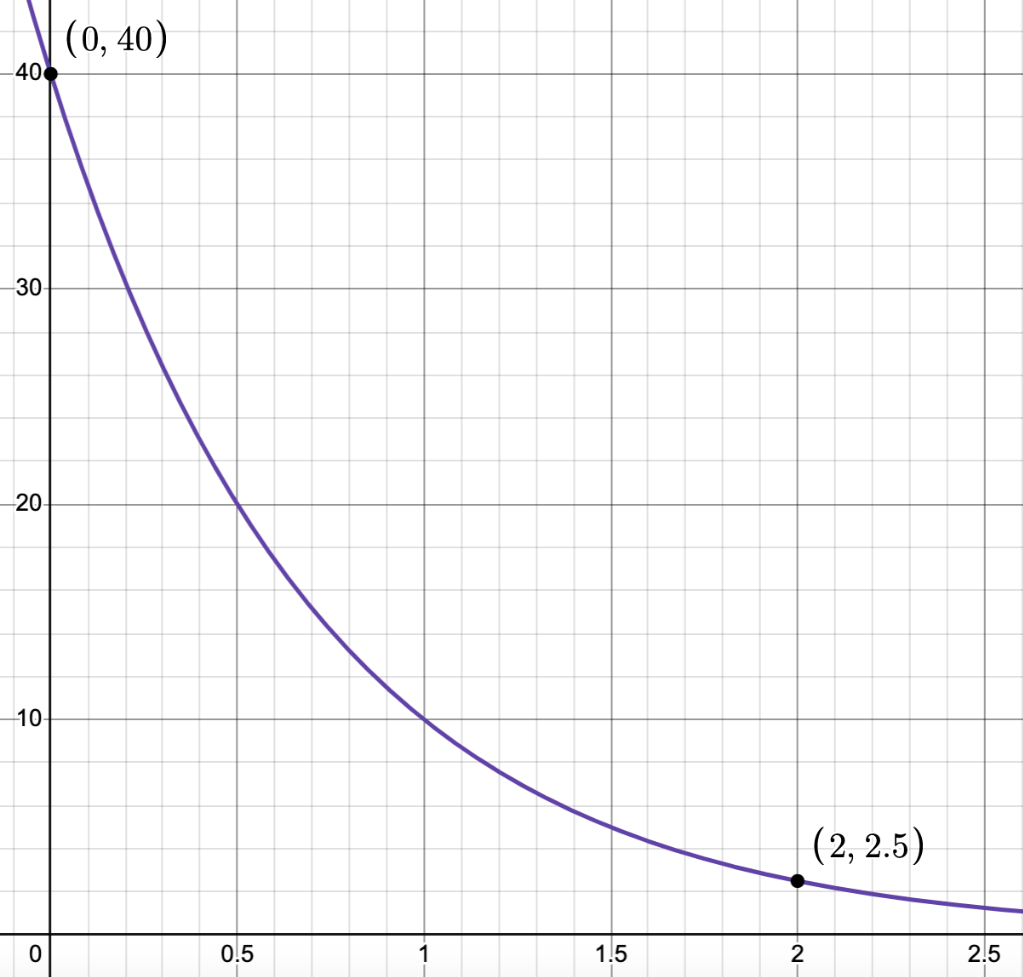
f(x) = 40 *0.25^x
The number of cell phones owned (in millions) is given by the function.
p(t) = 23*(1+0.12)^t
When will the number of cell phones reach 1 billion?
12.97 years