Arithmetic Sequences
Geometric Sequences
Probability: And, Or, Not
Probability: Two-Way Tables
Probability: Conditional Probability
100
Write the explicit definition of the arithmetic sequence shown in the table below:
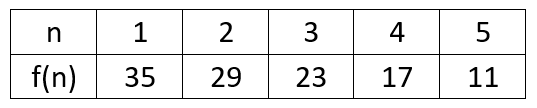
f(n) = 35 + (-6)(n - 1)
100
Find the 7th term of the geometric sequence:
6, 18, 54, ...
6, 18, 54, 162, 486, 1458, 4374
f(7) = 6 * (3)7 - 1
f(7) = 6 * 1458
f(7) = 4374
100
Event A is the Celtics win the NBA finals.
Event B is the Mavericks lose the NBA finals.
Are these events mutually exclusive or inclusive?
Inclusive
100
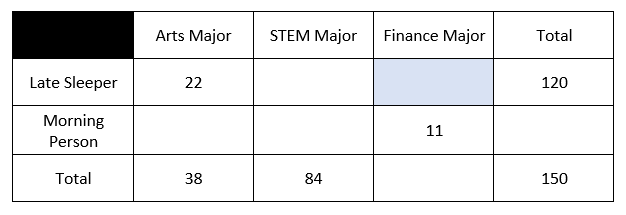
What number belongs in the shaded square?
There are 17 students who are late sleepers and finance majors.
100
Mr. Neri was flipping three coins. The first landed heads, and the other two landed on tails. Are these events independent or dependent?
Independent- they do not affect each other
200
An arithmetic sequence's first four terms are:
-42, -25, -8, 9
Write the recursive definition of this sequence.
f(1) = -42
f(n) = f(n - 1) + 17
200
Find the common ratio of the sequence below:
0.125, 0.375, 1.125, 3.375, 10.125
0.375/0.125 = 3 = r
200
The numbers 1, 2, 3, 4, 5, 6, 7, and 8 are placed in a bag. The probability that a number pulled at random will be less than 3 is P(A).
What is P(A')?
P(A') = 1 - P(A)
P(A) = 2/8.
Thus P(A') = 6/8.
200
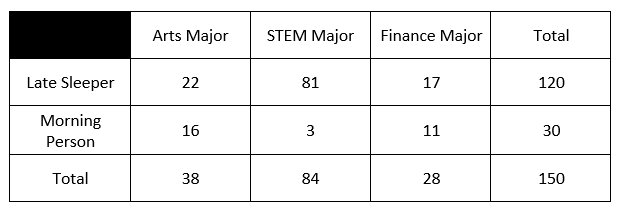
Find P(Morning Person or Arts Major).
P(MP or A) = (30 morning people + 38 arts majors - 16 overlap)/150 total = 52/150
200
Joey, Jimmy, Josephine, Johnny, Jeremy, and Jaime are candidates for class president, vice president, and secretary. Jaime won the election for class president. Assuming everyone has an equal chance, what is the probability that Jimmy wins the vice presidency?
1/5 = P(Jimmy VP | Jaime Pres)
300
What is the 11th term of the sequence below?
22, 29, 36, 43, ...
22, 29, 36, 43, 50, 57, 64, 71, 78, 85, 92
f(11) = 22 + (7)(11 - 1)
f(11) = 22 + 70
f(11) = 92
300
The explicit form of a geometric sequence is shown below:
f(n) = 2.54 * (4)n - 1
Write the recursive definition of this sequence.
f(1) = 2.54
f(n) = f(n - 1) * 4
300
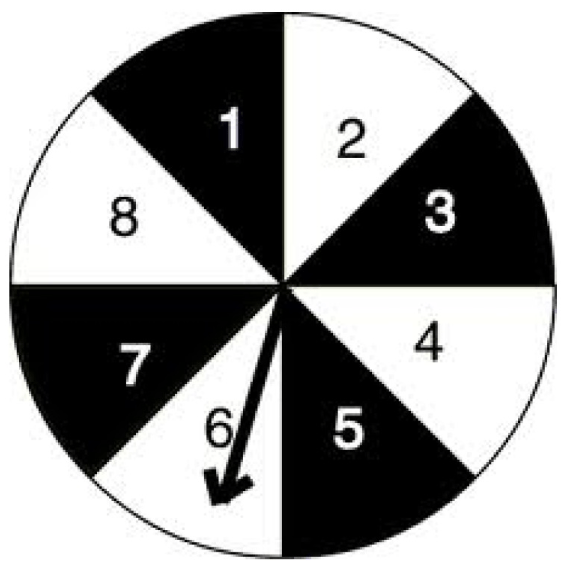
If using this spinner, find P(Black or Less than Six).
(4 black + 5 less than six - 3 black AND less than six)/8
6/8 = P(Black or Less than Six)
300
Find the relative frequency of STEM majors who are late sleepers.
81/150 = 54%
300
Mr. Neri was sharing a pizza with Mrs. Neri. After Mr. Neri put the pizza on the table, their dog Murphy jumped up and stole a piece! After that, Mr. Neri had a 1/7 chance to pick a pepperoni slice. Which slice did Murphy steal?
Pepperoni
400
Mr. Neri was making grilled kielbasa at a barbecue.
The number of pieces of kielbasa is given as the arithmetic sequence:
f(n) = 5 + (3)(n - 1)
where n is the number of guests who attend the barbecue.
How many pieces should Mr. Neri cook if there are 8 guests?
f(8) = 5 + (3)(8 - 1)
f(8) = 5 + 21
f(8) = 26 pieces of kielbasa
400
Mr. Neri bought 2,000 pencils at the start of the year. Every school day, he loses 4%. How many pencils will he have left after 166 school days?
f(n) = 2000 * (0.96)n - 1
f(166) = 2000 * (0.96)166 - 1
f(166) = 2 pencils
400
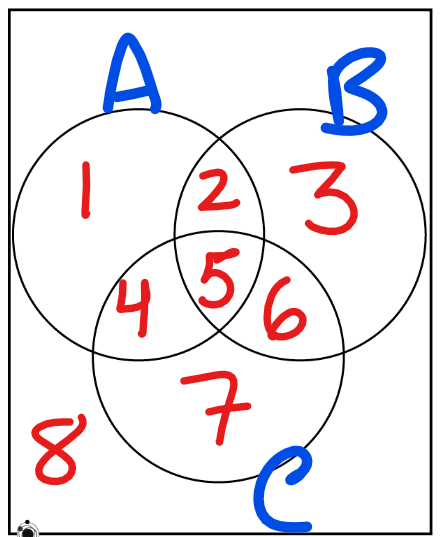
On this Venn diagram, which numbered areas would be shaded for P(A')?
Everything not in circle A: 3, 6, 7, 8
400
If a student is selected at random, what is the probability that they are a late sleeper given that they are a finance major?
P(LS | FM) = 17/28
400
A bag contains 3 blue, 3 red, 3 green, and 5 yellow chips. After a chip is removed, it is not replaced.
Sheldon picked a red chip.
Janelle picked a green chip.
What is the probability that Jordan now picks a chip that is not blue?
P(Not Blue | Red 1st, green 2nd) = 9/12