Graph Me
Solve Me
Change Me
What about Me
Miscellaneous Me
100
What is the equation of the quadratic in Vertex Form?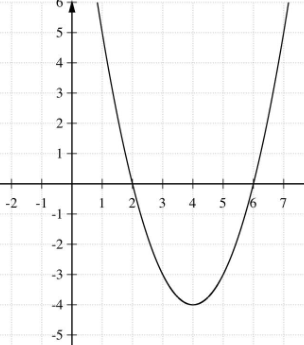 
f(x) = (x - 4)^2 - 4
100
Solve the Quadratic Equation
3x^2 + 9x = 12
x =-4; x = 1
100
The equation of a quadratic in vertex form is
V(x) = -(x - 2)^2 + 1
Write the equation of the quadratic in Standard and Factored form.
Standard Form
S(x) = -x^2 +4x - 3
Factored Form
F(x) = -(x -1)(x - 3)
100
What would be the end behavior and roots of the polynomial function
f(x) = -x^3 - 7x^2 - 6x
Roots:
x = 0, x =-6, x =-1
End Behavior: Up / Down
x->-oo; y -> oo
x->oo; y -> -oo
100
multiply the imaginary terms and write your final answer as
a + bi
(3 + 2i)(3 - i)
11 + 3i
200
Sketch the parent graph for a radical function.
200
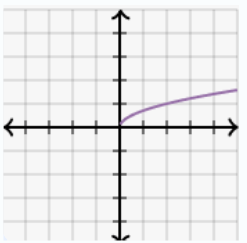
Solve the radical equation.
2sqrt(x + 11) + 1 = 7
x = -2
200
Simplify the Polynomial by multiplying them together. Write your answer in standard form.
(x^2 + 3x - 4)(x - 6)
x^3- 3x^2 - 22x + 24
200
What would be the Domain and Range for the Radical function
f(x) = sqrt(x+2) - 5
Domain:
[-2, oo) or x ≥ -2
Range:
[-5,oo) or y ≥ -5
200
Find
f(g(2)) =
f(x) = 3x + 5
g(x) = x^2 +4
f(g(2)) = 29
300
In a graph what do we call a boundary line that a function can approach but never touch or cross? Found in exponential functions, log functions, and rational functions.
Asymptote
300
Solve the exponential using a common base.
4^(3x - 1) = 16^(x + 3)
x = 7
300
Simplify the radical
root(4)(81x^8y^5
3x^2 y root(4)(y)
300
What is the vertex of the quadratic and is it a max or min?
f(x) = x^2 + 12x + 14
Vertex is a Min at (-6, -22)
300
Use the table to answer the question
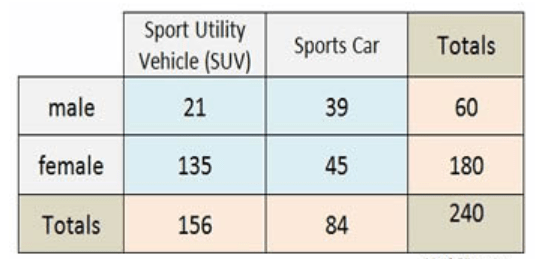
Given that the customer is a male, what is the probability they are buying a sports car?
P("sport" | "male") = 39/60 =0.65 = 65%
400
Name the polynomial graphed by degree.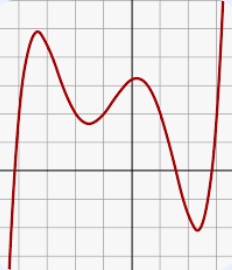 
5th Degree Polynomial also called a Quintic Polynomial.
400
Solve the log equation. Check for extraneous solutions.
2log(x) = log(4x + 12)
Solution
x = 6
Extraneous solution
x = -2
400
Write the exponential in log form.
3(2)^x = 4
log_2(4/3) = x
log_2(4) - log_2(3) or 2 - log_2(3)
400
What is the equation of a log function that is decreasing with a Vertical Asymptote at x = -3
Option 1
f(x) = -log(x + 3)
Option 2
f(x) = log_(1/10)(x + 3)
400
To win a game of cards against your friend you need to draw a card greater than 4, then a card greater than 8. Assuming you have 26 Standard deck of cards left, what is the probability of winning the game?
P(> 4) P(>8)
(9/26)(5/25) = 7%
500
Describe the transformation of the parent graph
f(x) = 1/x
to result in the new equation
g(x) = 1/(x - 6) + 2
The graph has a Horizontal Translation of 6 (Shift right 6) and a Vertical Translation of +2 (Shift up 2)
Honors: The Vertical Asymptote shifted to x = 6 the Horizontal Asymptote shifted to y = 2
500
Solve the rational equation. Check that your solution is in the Domain.
(x + 5)/(x) = (x + 3) /(x + 2)
x = -5/2 or -2.5
500
Divide the polynomial using any method. Write your answer in standard form.
(x^4-23x^2-2x - 50) /(x + 5)
x^3 - 5x^2 + 2x - 12 + 10/(x + 5)
500
Given function f can be represented by equation
f(x) = (x + 3)^2 - 7
What would be
f^-1(9) =
f^-1(x) = sqrt(x + 7) - 3
f^-1(9) = 1
500
Give an example of an extraneous solution.
Answer varies: Extraneous solutions happen when the algebraic answer is not in the function's domain. When you check your answer you get a domain Error.
Example 1: Take the log of 0 or a negative
log(-3)
Example 2: Square root of a negative
sqrt(x - 3) " when x = -4"
Example 3: Dividing by zero.
1/(x + 5); x = -5