What is the domain and range of this function? Give your answer in interval notation.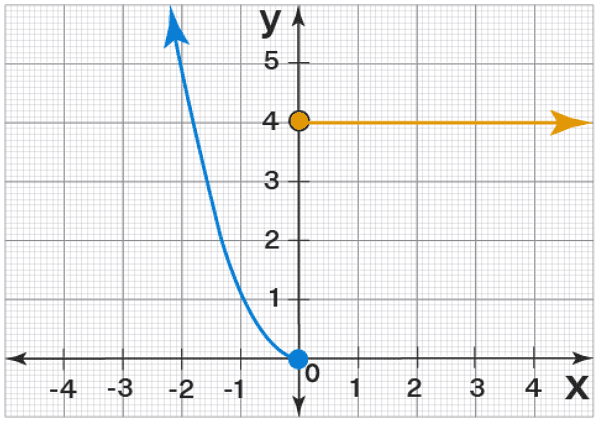
domain: (-∞,∞)
range: [0,∞)
Describe the relationship between number of games and score.

As the number of games increases, the score increases.
Solve 3 + |2x| = 7
x = 2, -2
Solve x2 + 6x + 8 = 0.
Find the difference:
5x2 - 4x + 3 - (2x2 - 7x + 8)
3x2 +3x -5
What are the x-intercepts (zeros) and y-intercepts of this function?

X-intercepts (zeros): x = -2 (x = 2 is NOT because there is a hole)
Y-intercepts: y = 4
State the parent function and describe the transformation(s).
y = x + 5
parent function: linear
transformations: shift up 5 units
Solve the following absolute value inequality:
2|x| ≤ 8
-4 ≤ x ≤ 4
Complete the following operation:
5i + 3 - (4i - 6)
i + 9
Find the product:
(5x - 4)(3x2 - x + 2)
15x3 - 17x2 +14x - 8
For which intervals is this function increasing and decreasing?
Increasing: (-4,0)
Decreasing: (0,4)
State the parent function and describe the transformation(s).
y = 3x2 - 7
parent function: quadratic
transformations(s): vertical stretch by a factor of 3, shift down 7 units
Solve 3 - |5x| = 8
No solution, absolute value can't be negative
Find the solutions of the following system of equations:
x + y = 5
y = x2 − 25
(5,0) and (-6,11)
Simplify the following rational expression:
(x-1)/(x-5)
At which point on this graph does the absolute maximum occur?

(0,4)
Determine the equation for the line of best fit for this data and use it to estimate the number of gallons bought when someone spends $6.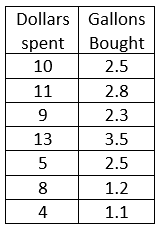
Equation for the line of best fit: y = 0.198x + 0.575
gallons: 1.76
Ms. Cislo sets her coffee maker to brew coffee so it is ready when she wakes up in the morning. The proper brewing temperature for coffee tea is 210º F plus or minus 5 degrees. Write and solve an absolute value equation representing the maximum and minimum brewing temperatures for coffee.
Equation: |x – 210| = 5
Case 1: x – 210 = 5, so x = 215
Case 2: x – 210 = -5, so x = 205
Solutions:
x = 205 (minimum temperature)
x = 215 (maximum temperature)
Solve -2d2 + 3d - 5 = 0
x = (-3 ± i√31)/-4
Find the quotient:
2(x+6)/(3x-2)
What is the end behavior of this function?
As x → ∞, f(x) → 4
As x → -∞, f(x) → ∞
If the equation y = √(x + 1) - 3 is translated right 3 units, up 1 unit, reflected across the y-axis, and stretched vertically by a factor of 2, what is the resulting equation?
y = 2√(-x - 2) - 2
At the Brooks Company, the average starting salary for a new employee is $37,600, but the actual salary could differ from the average by as much $2590. Write an absolute value inequality to describe this situation and solve the inequality to find the range of the starting salaries.
Inequality: |x – 37600| ≤ 2590
Case 1: x – 37600 ≤ 25900, so x ≤ 40190
Case 2: x – 37600 ≥ −25900, so x ≥ 35010
Solution: $35,010 ≤ x ≤ $40,190
Solve the following quadratic inequality:
x2 - 6x - 9 < 7
-2 < x < 8

(-3x+2)/[(x+2)(x-1)(x-2)]
