Function Notation
Linear Functions
Sequences
Exponents and Roots
Radical Equations
Quadratics
100
f(x) = 30x - 14
f(2) = ?
f(2) = 30*2-14 = 46
100
Write an equation of a line that has a slope of 3 and a y-intercept of -4
y = 3x - 4
100
Is the following sequence arithmetic, geometric, or neither?
10, 7, 4, 1, -2, -5, ...
Arithmetic (subtract 3 each time)
100
What value should replace the variable:
(4^x)^3 = 4^18
x = 6
100
Solve the following equation:
x^2 = 36
x = 6 or -6
100
Set up (don't solve or simplify) the quadratic formula for this equation:
2x^2 + 5x - 1 = 2
x = (-5 +- sqrt(5^2-4(2)(-3)))/(2(2))
200
Is this graph a function - yes or no?
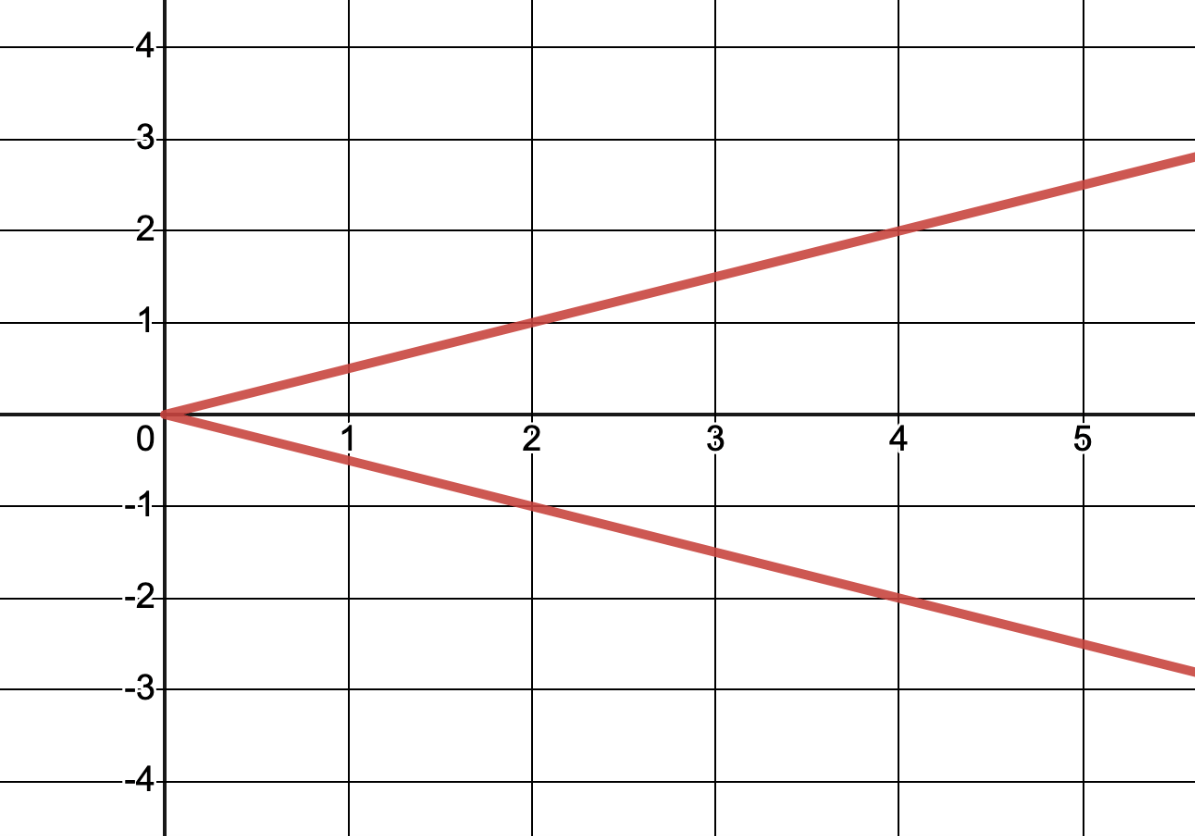
No!!!!
200
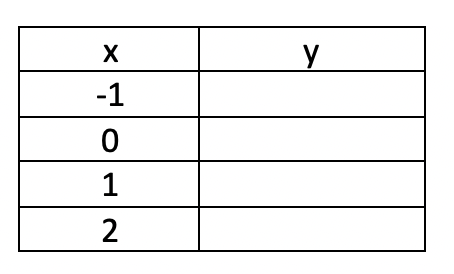
Fill out the following table for the equation
f(x) = 4x - 5
200
Write the next 3 terms of the sequence:
2, -4, 8, -16, ...
2, -4, 8, -16, 32, -64, 128
200
Put
root(6)(7^14)
into exponential form.
7^(14/6)
200
Solve the equation:
root(3)(x+5) = -2
x = -13
200
What are the solutions to the following quadratic equation
(x+6)(x-2)= 0
x = -6, 2
300
f(x) = (x^2+2)/(x-1)
f(2) = ?
f(2) = (2^2+2)/(2-1) =6
300
Find the slope between the points
(3, 0) and (4, 2)
m = (2 - 0) / (4 - 3) = 2/1 = 2
300
Write the first 5 terms of the sequence given the following formula:
f(1) = 8
f(n) = f(n - 1) + 3/2, n >= 2
8, 9.5, 11, 12.5, 14
300
5^(3/4)
in radical form
root(4)(5^3)
300
Solve the equation for x:
4(x-1)^3 = 108
x = 4
300
Factor the following quadratic:
x^2 +4x - 5
(x - 1)(x + 5)
400
Find the value(s) of x such that g(x) = 3
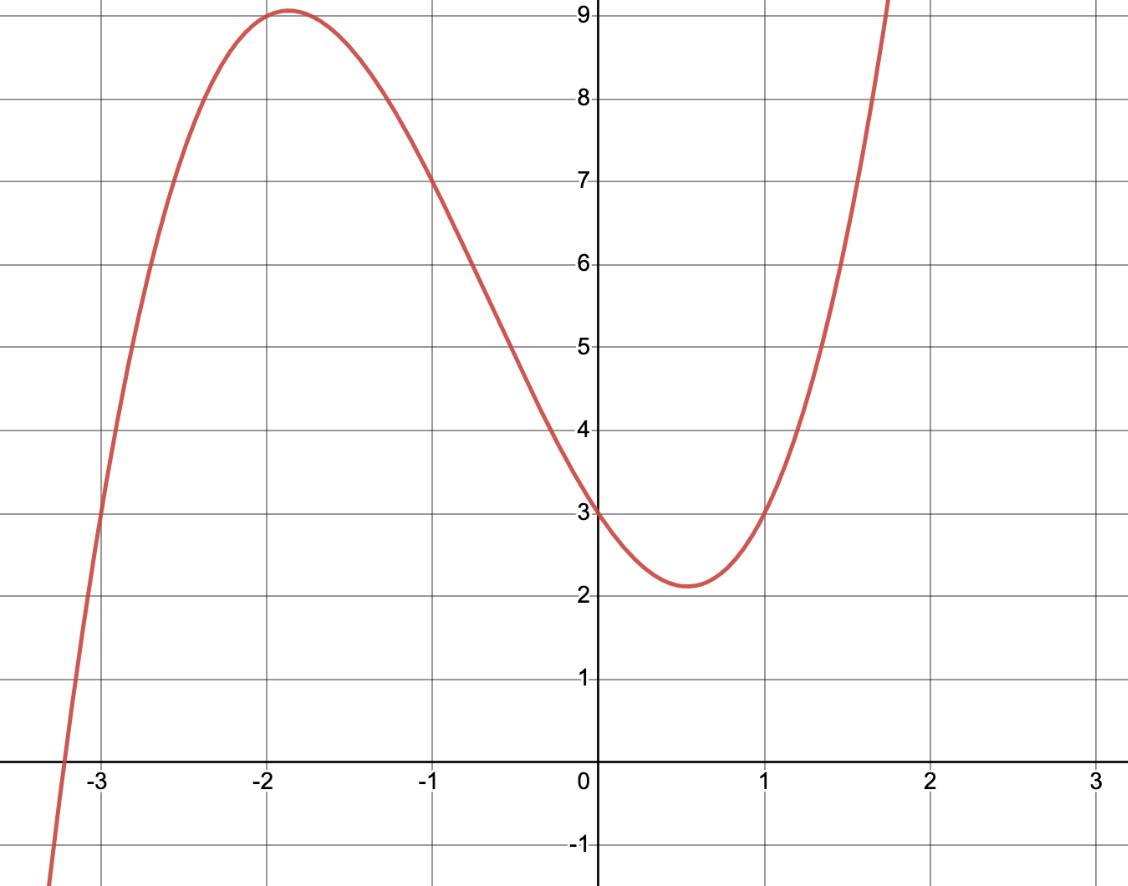
x = -3, 0, and 1
400
Write the equation of the line that would create this table:
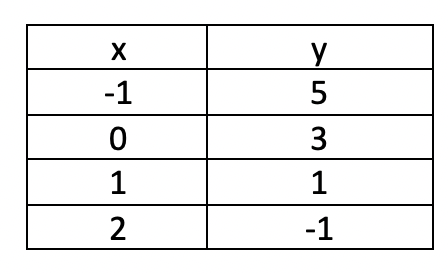
y = -2x + 3
400
Write and explicit formula for the following sequence:
3, 30, 300, 3000, ...
f(n) = 3 * 10^n, n >= 0
400
What value should replace the variable:
1/3 = 9^x
x = -1/2
400
Solve the following equation:
sqrt(2x -10) + 2 = 8
x = 23
400
Solve the following quadratic equation using whatever method you like:
2x^2+6x+12 = 8
x = -2 or -1
500
The temperature T of a room is a function of the number of hours h a heater has been running. Convert the following sentence to function notation:
T(6) = 82
500
Write the equation of the following line
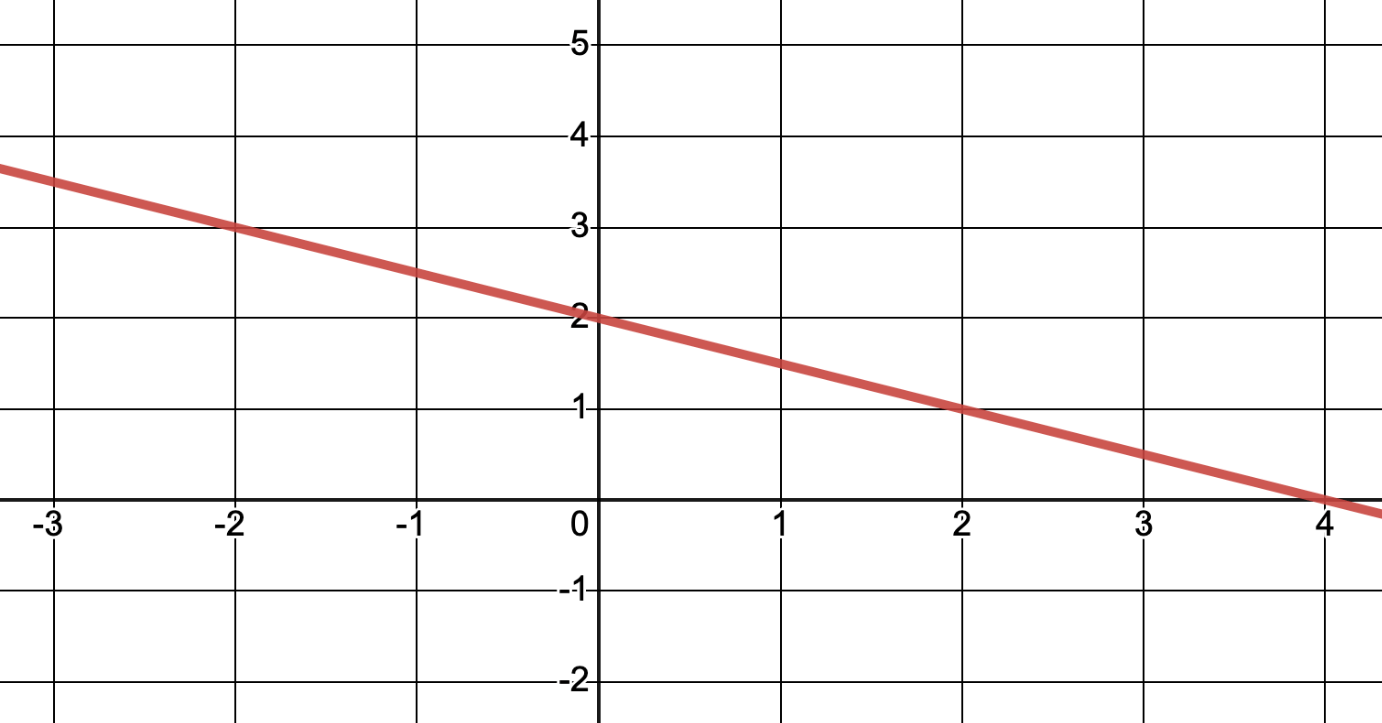
y = -1/2x + 2
500
Write an explicit formula for the following sequence:
f(n) = (n+1)^2, n>=1
500
Use exponent rules to simplify this expression until it can be written without exponents:
(2^3*5^3)/10^4
1/10
500
Put this radical into simplest form:
sqrt(9/7)
(3sqrt(7))/7
500
Factor the following expression
9x^2 + 24x + 16
(3x+4)^2