Evaluating and Composing Functions
Transforming Functions
Inverse Functions
Rational Exponents and Roots
Complex Numbers
Quadratics
100
f(x) = (x^2+2)/(x-1)
f(2) = ?
f(2) = (2^2+2)/(2-1) =6
100
Describe the transformation that happened from the parent function (dashed) to the new function (solid).
Tell what kind of transformation, what direction, and how much (if applicable).
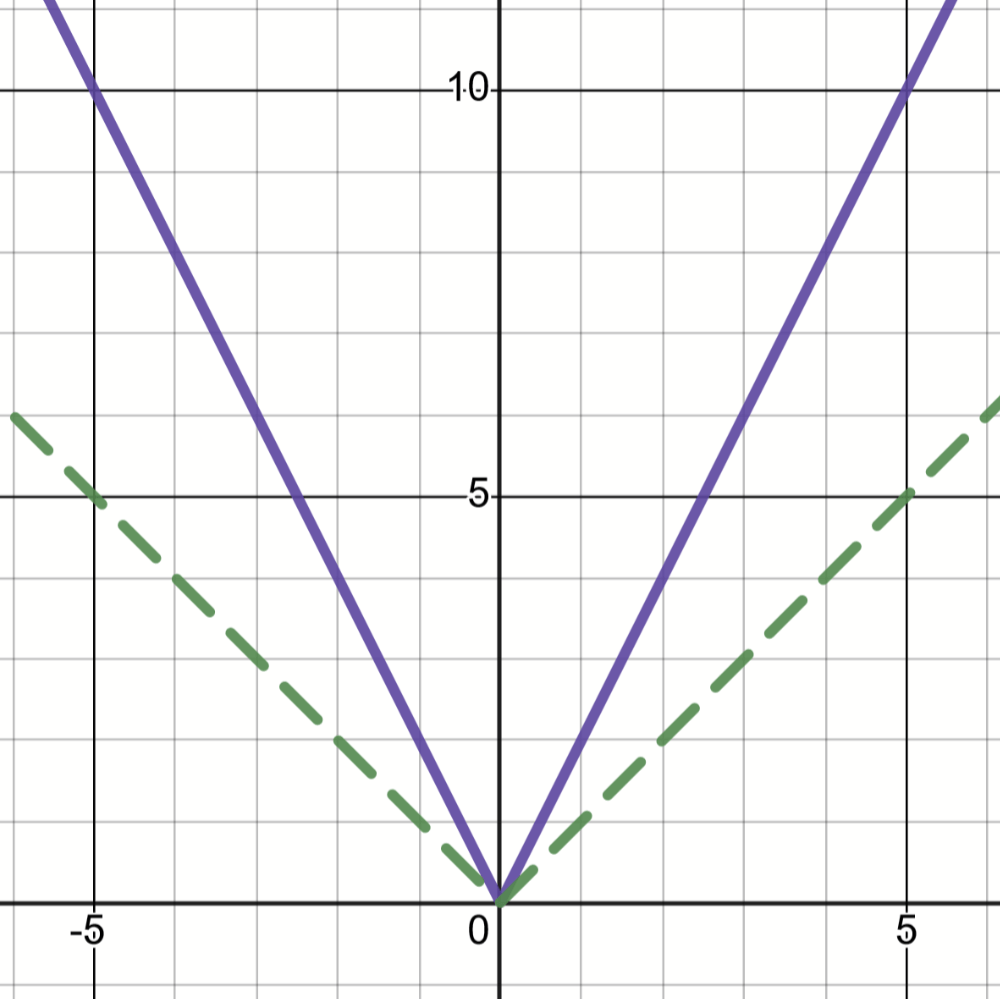
Vertical stretch by a factor of 2
100
The graph of f(x) contains the point (4,-6), so f-1(x) contains the point ...
(-6,4)
100
5^(3/4)
in radical form
root(4)(5^3)
100
sqrt(-16)
written using i4i
100
Set up (don't solve or simplify) the quadratic formula for this equation:
2x^2 + 5x - 1 = 2
x = (-5 +- sqrt(5^2-4(2)(-3)))/(2(2))
200
f(x) = 30x - 14
f(2) = ?
f(2) = 30*2-14 = 46
200
Describe the transformation that happened from the parent function f(x) to the new function g(x).
Tell what kind of transformation, what direction, and how much (if applicable).
f(x) = x^2
g(x) = x^2 - 5
Translation down 5 units
200
f and g are inverses. g(f(5)) = ?
5
200
Put
root(6)(7^14)
into exponential form.
7^(14/6)
200
(18 + 10i) + (3 - 7i)
21 + 3i
200
How many solutions does this equation have?
4x^2 - 12x + 9 = 0
1 solution
300
f(x) = -x+4
g(x) = x/3
g(f(10)) = ?
f(10) = -10+4 = -6
g(-6) = -6/3 = -2
g(f(10)) = -2
300
Describe the TWO transformations that happened from the parent function (dashed) to the new function (solid).
Tell what kind of transformation, what direction, and how much (if applicable).
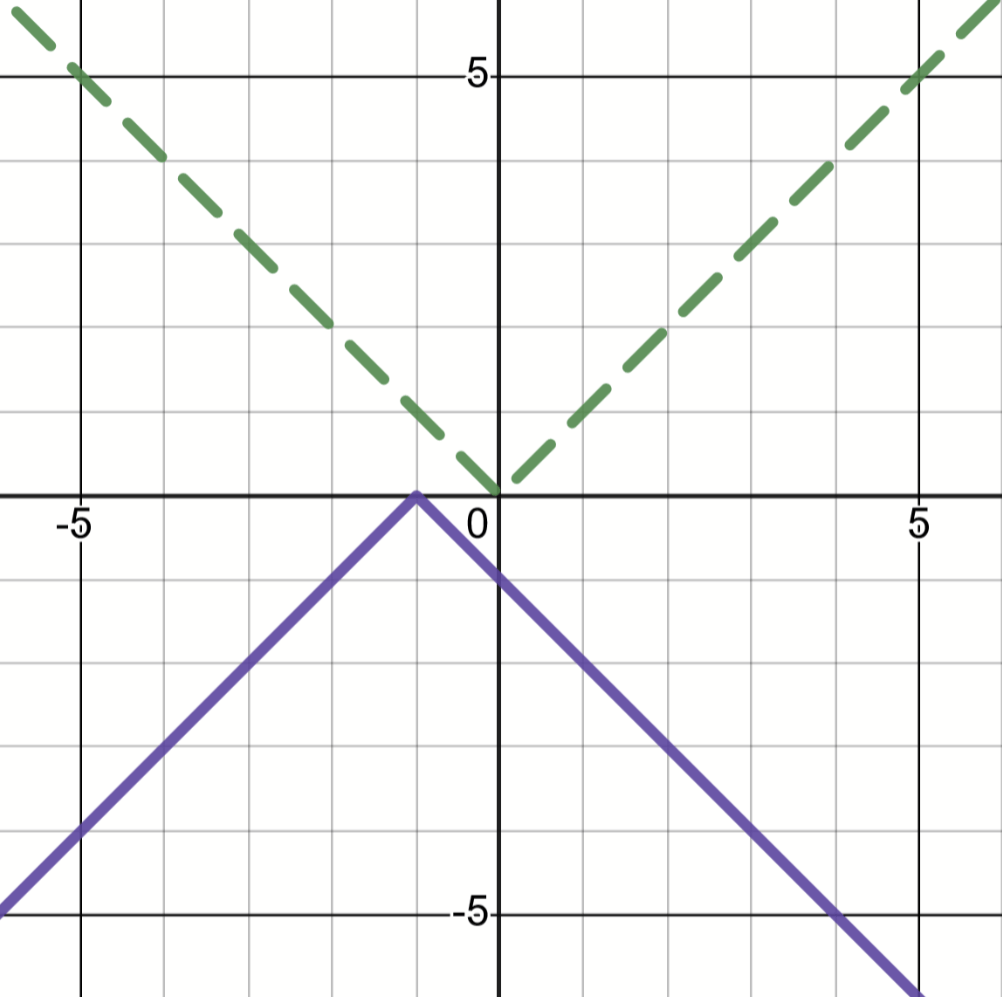
Reflection across the x-axis (vertical reflection)
and
Translation 1 unit left
300
Find inverse of function
f(x) = 2x + 1
f^(-1)(x) = (x-1) / 2
300
**DOUBLE JEOPARDY**
Put this radical into simplest form:
sqrt(9/7)
(3sqrt(7))/7
300
(-1 + 5i) - (4 + 2i)
-5 +3i
300
What are the x- and y- intercepts of the following quadratic equation?
y = (x+6)(x-2)
x-intercepts at -6, 2
y-intercept at -12
400
f(x) = 7x
g(x) = |x - 4|
g(f(x)) = ?
g(f(x)) = |7x-4|
400
Write the equation that represents
f(x) = x^2
horizontally stretched by a factor of 3.g(x) = (1/3x)^2
400
Graph the inverse of the following function:
400
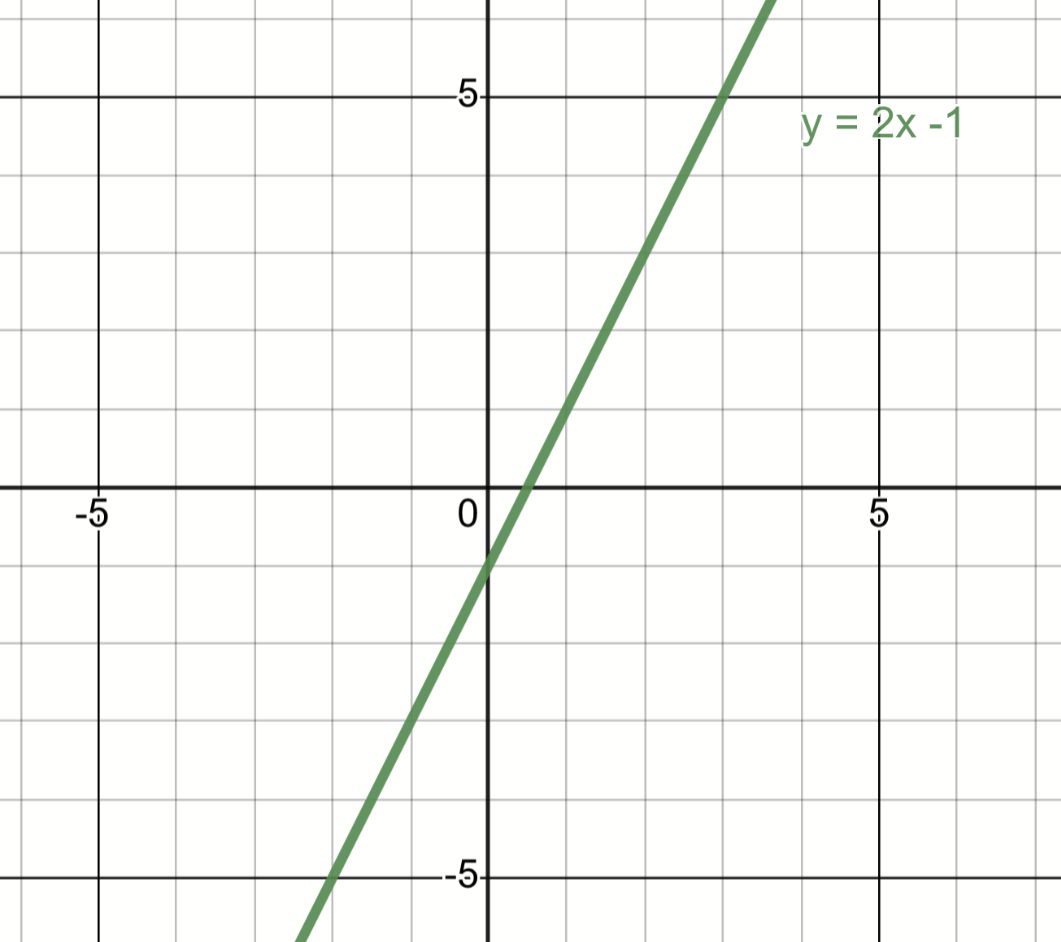
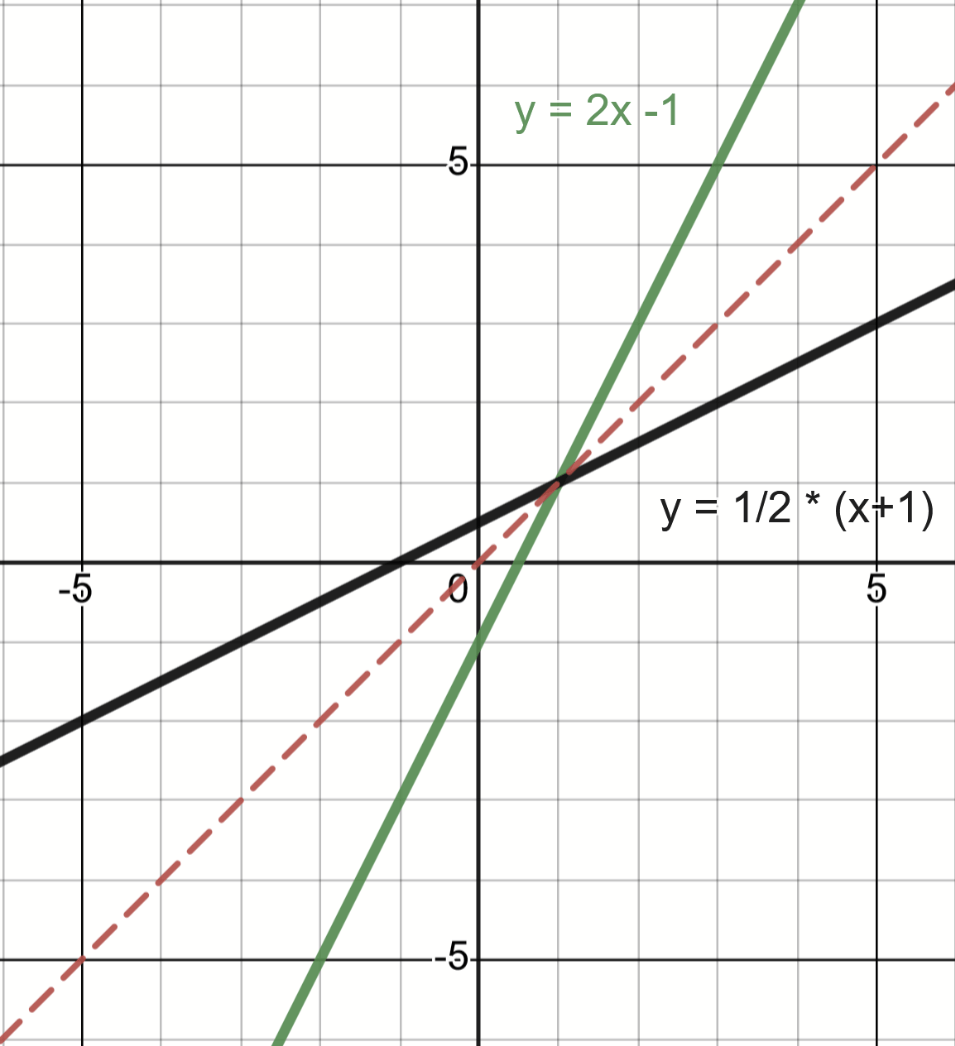
Solve the following equation:
sqrt(2x -10) + 2 = 8
x = 23
400
8i(5 +2i)
-16 + 40i
400
Solve the following quadratic equation using whatever method you like:
2x^2+12 = 8 - 6x
x = -2 or -1
500
f(x) = x/5
g(x) = x - 6
h(x) = |x|
h(g(f(x))) = ?
h(g(f(x))) = |x/5-6|
500
Write the equation that represents
f(x) = x shifted up 8 units and reflected horizontally across the y-axis.
g(x) = (-x) +8 or -x + 8
500
Find inverse of function
g(x) = (3x - 5)/4
g^(-1)(x) = (4x + 5)/3
500
Simplify the following expression using exponent rules:
(2^3*5^3)/10^4
1/10
500
(3 - 2i)(9+5i)
37 - 3i
500
Factor the following expression
9x^2 + 24x + 16
(3x+4)^2