What is the degree of the polynomial
f(x)=5x^4-2x^3+7?
4
Before multiplying, expand (x-5)^4
(x-5)(x-5)(x-5)(x-5)
Name the identity:
(a+b)(a-b)
Difference of Squares
a^2-b^2
If we divide P(x)=x^3-5x^2+2x+8 by (x-4) we get x^2-x-2 .
What are the two factors that express P(x) as a product?
(x-4)(x^2-x-2)
What happens to y=f(x) after it has been transformed to y=f(x)+3?
Shift up 3.
How many turning points does this polynomial have?
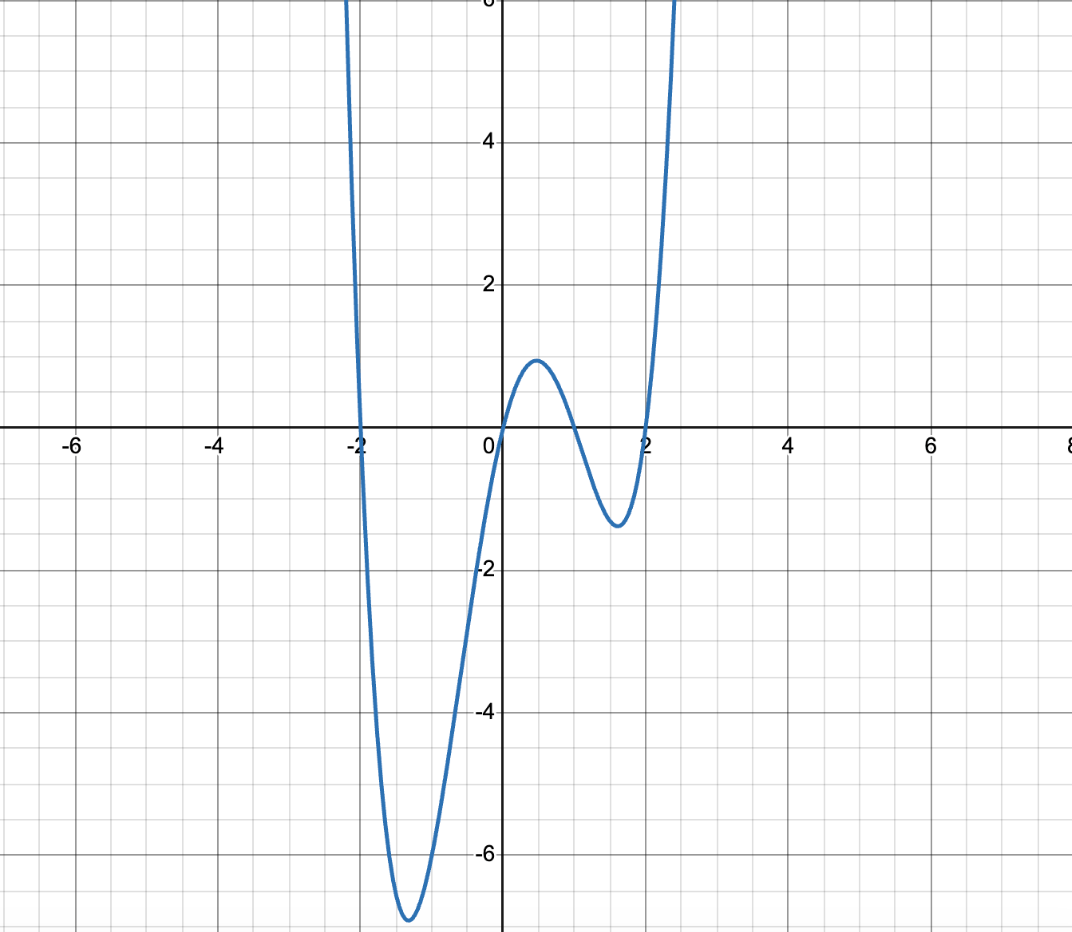
3
Expand:
(2x-3)^2
(2x-3)(2x-3)
4x^2-12x+9
Fill in the missing signs (+/-) to the following polynomial identity:


Given: (x-3)^2(x+1)^3
What are the zeros, its multiplicity and describe if it bounces or crosses.
x=3
Multiplicity: 2 | Bounces (even multiplicity/exponent)
x=-1
Multiplicity: 3 | Crosses (odd multiplicity/exponent)
How does the graph of the function
f(x)=6x^7-2 differ from the graph of its parent function?
Shifted down 1, stretched by a factor of 6.
What can you say about the degree and sign of the leading coefficient of the graph below?
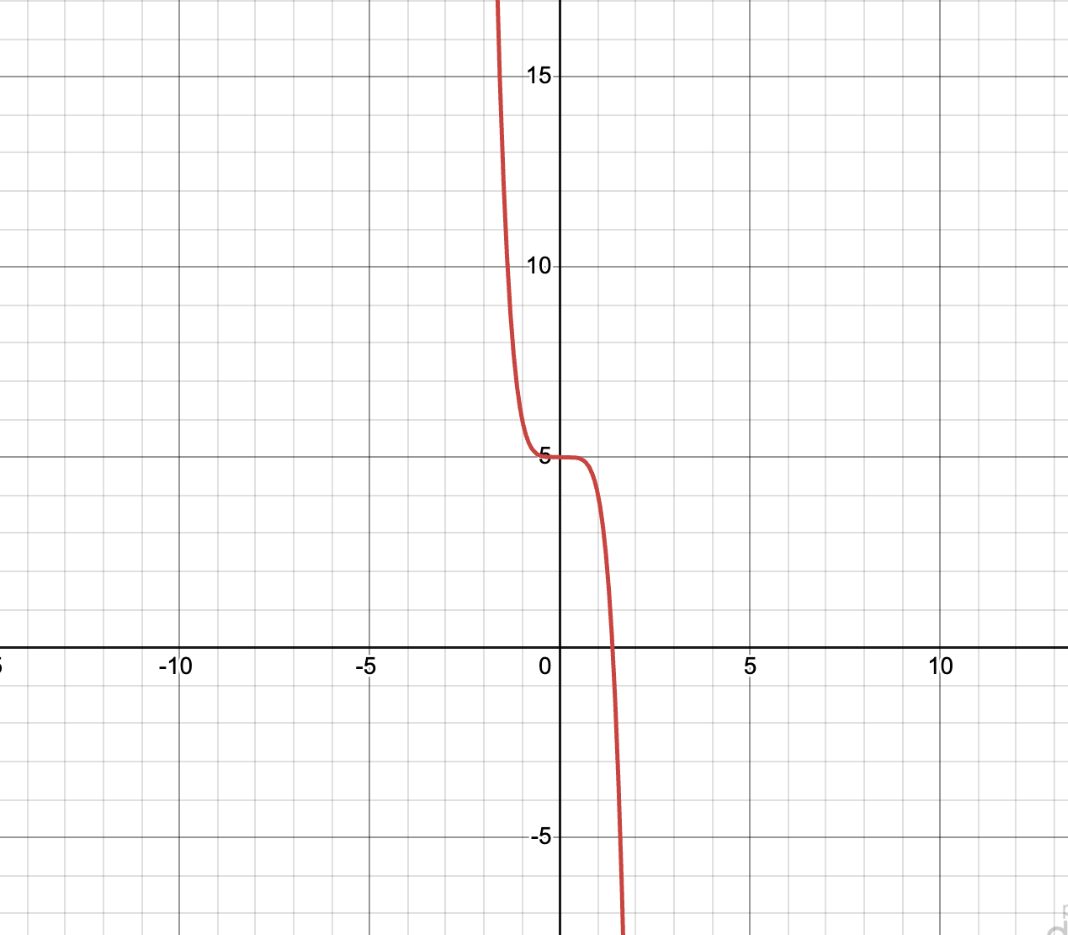
Odd degree, negative leading coefficient.
Multiply
(3x-2)(x+7)
3x^2+19x-14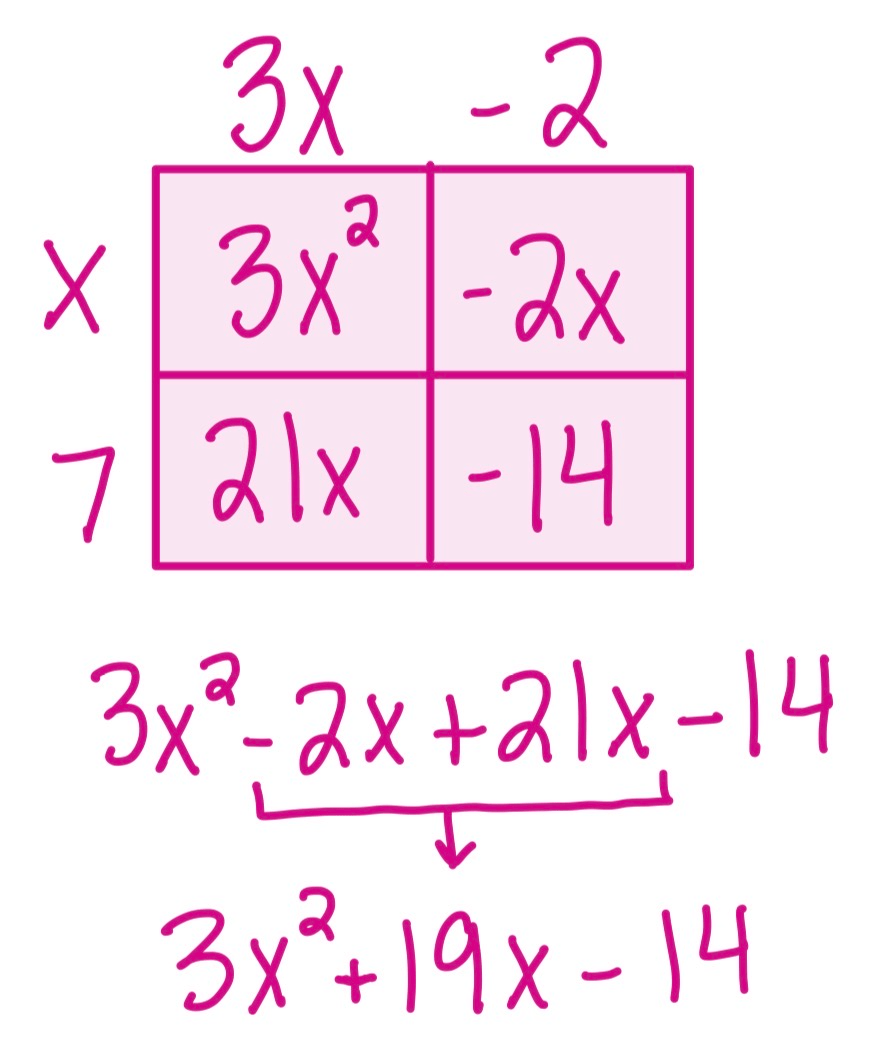
Simplify using an identity:
(x-5)(x+5)
x^2-25
If f(2)=0 , what factor must f(x) have?
(x-2)
The graph of f(t) models the height, in feet, that a bee is flying above the ground with respect to the time it traveled in t seconds.
What is the average rate of change over the interval [2,10] ?
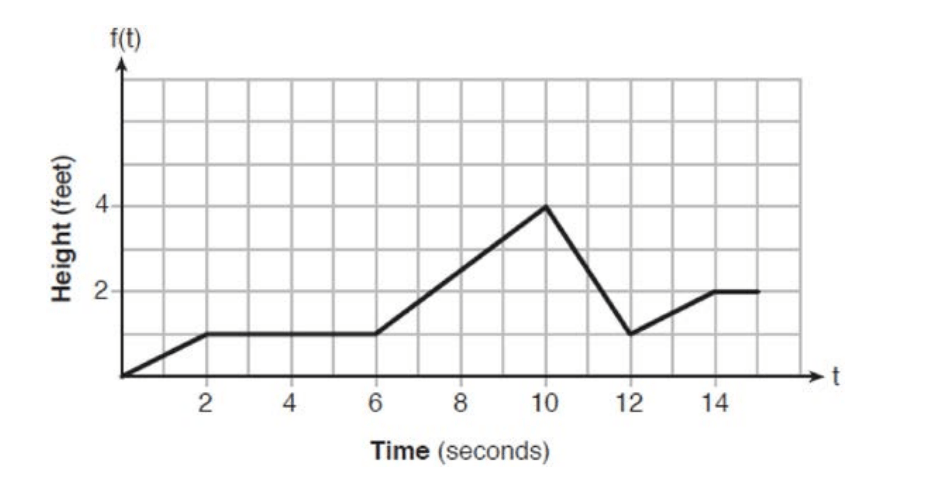
3/8
True or False: A polynomial of degree 5 can have at most 5 real zeros.
True!
Multiply
(x^2+6x-7)(2x+2)
2x^3+14x^2-2x-14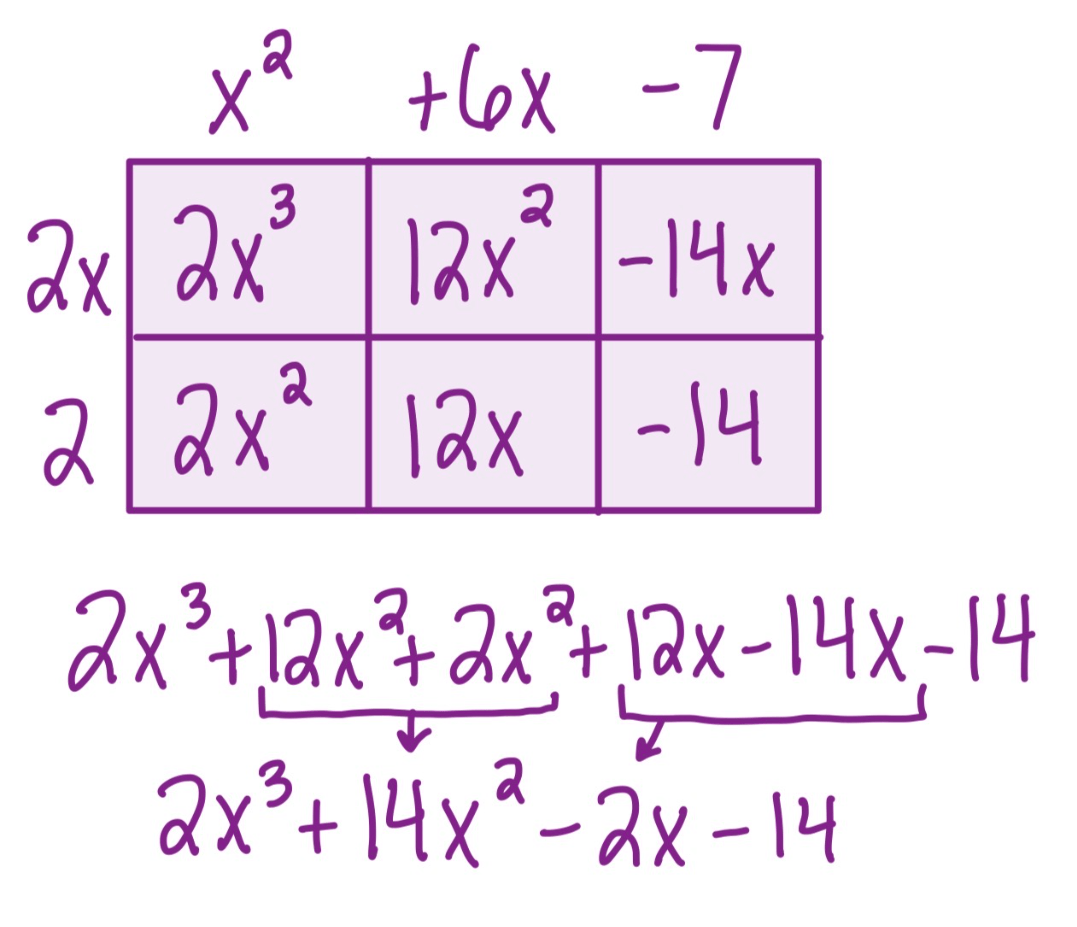
A medium-sized shipping box has side lengths s units, so its volume is s^3 cubic units.
A) A large box has side lengths that are 4 units longer than the medium box. Write a binomial expression to find the volume of the large box.
(s+4)^3
Identify the number of real and imaginary zeros f(x) has.
f(x)=2x^4+5x^3+3x^2+15x-9
2 real, 2 imaginary
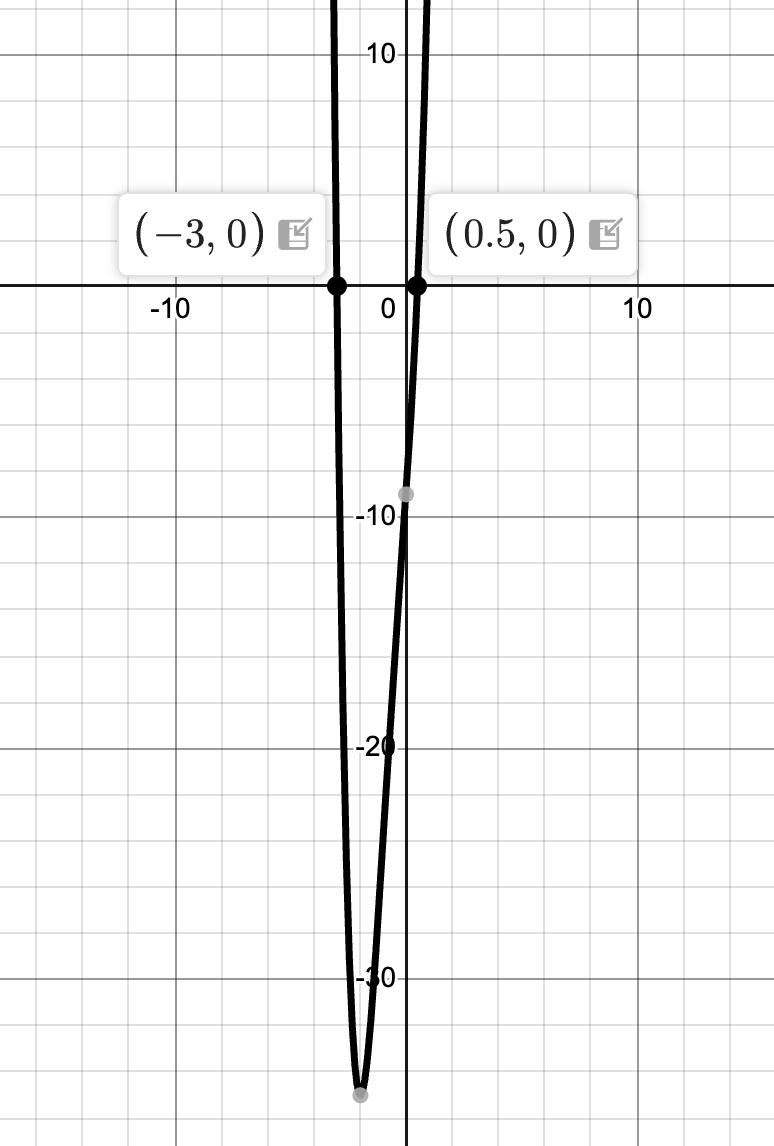
Describe all the transformations for g(x)=-2(x-1)^3+4 from f(x)=x^3.
Reflect x-axis, stretch by a factor of 2, right 1, up 4.
Describe the end behavior of the graph: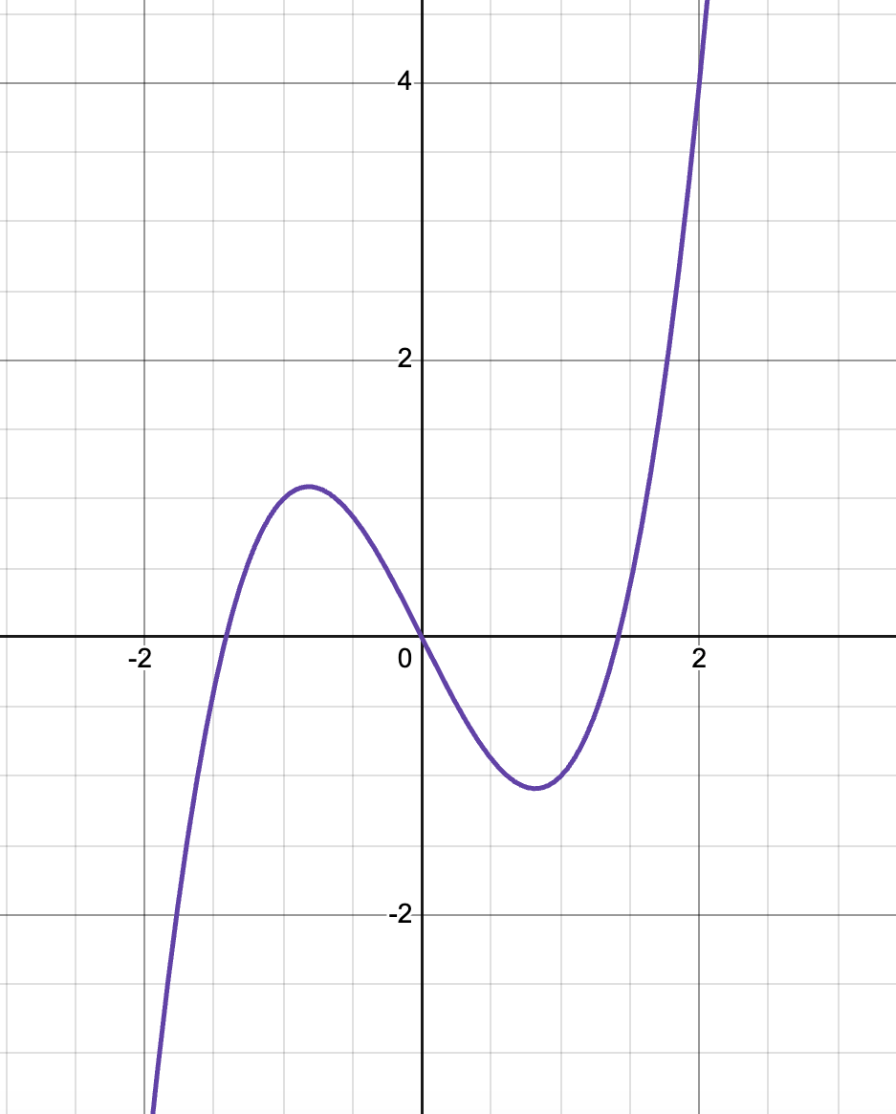
As x -> -∞, f(x)-> -∞
As x->∞,f(x)->+∞
Pascal's Triangle: What are the coefficients of
(a+b)^4
1, 4, 6, 4, 1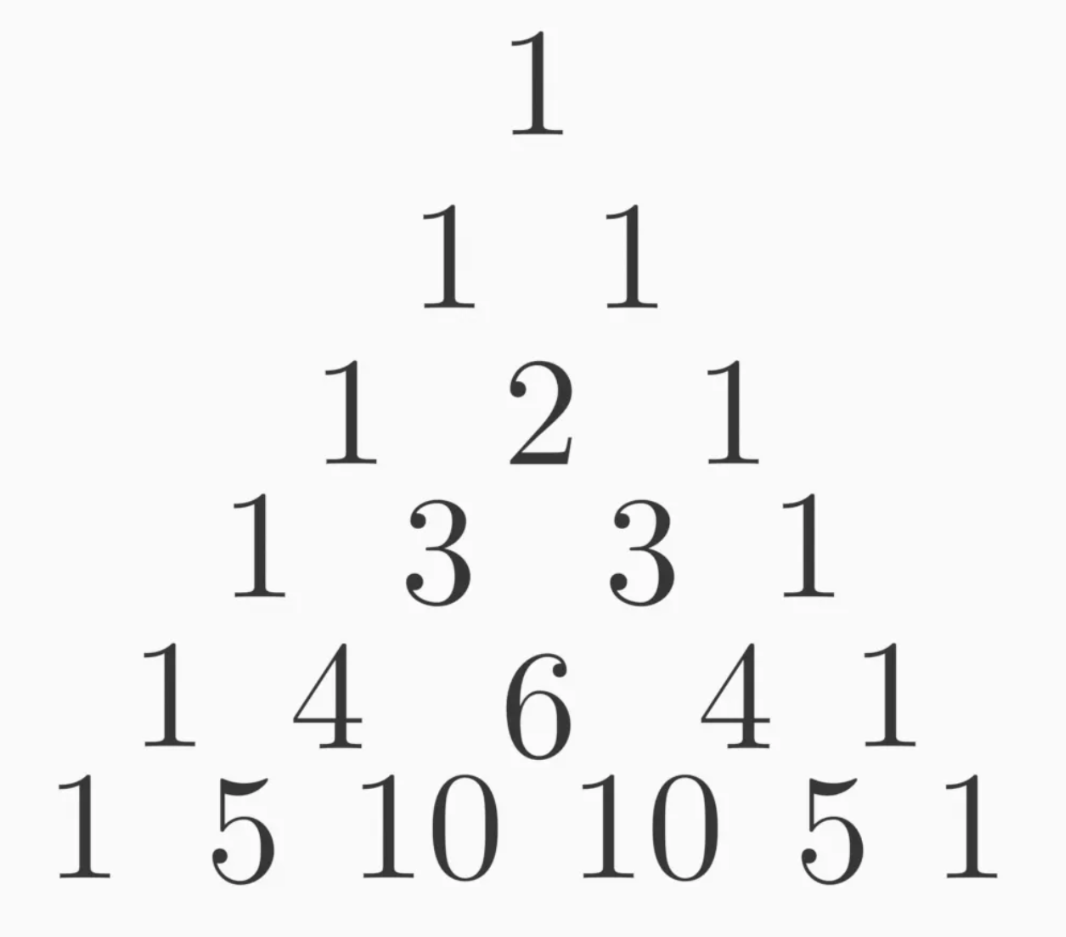
Factor:
27x^3+8

Using synthetic division divide x^3+7x^2+10x-6 by x+3.
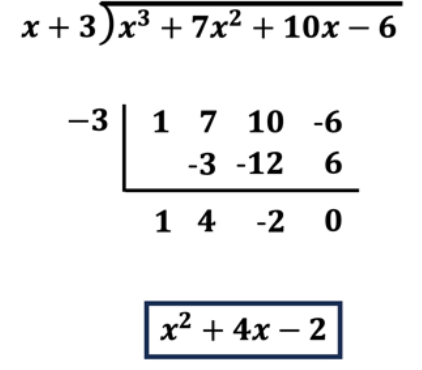
A graph touches at x = –1 and crosses at x = 2 and 4. Write one possible function.
Example: f(x)=(x+1)^2(x-2)^3(x-4)