Pre-Calculus
Domain & Range
Linear Functions
Slopes & Points
Absolute Value
100
The domain (x-values) in which a function (y-values) is increasing or decreasing.
What are Intervals of Increasing & Decreasing?
100
How far up and down our graph goes
What is the range?
100
The point in which a linear function crosses the y-axis
What is the y-intercept?
100
The coefficient of x for linear equations in slope-intercept form
What is the slope?
100
The values of x where |x| = 4/3
What is -4/3 and 4/3?
(negative four thirds and positive four thirds)
200
The troughs and peaks, the high-points and low-points, the change from positive slope to negative slope or vice versa
What are relative extrema?
200
The input or numbers we are allowed to put INTO a function
What is the domain?
200
The domain and range for all LINEar functions in interval notation
What is (-∞ ,∞ ) ?
(negative infinity to positive infinity)?
200
The b-term for equations in slope-intercept form
What is the y-intercept?
200
The parent equation for all Absolute Value equations
What is y=|x|?
(y equals the absolute value of x)
300
When the slope changes from negative to positive resulting in a trough or low point on a graph
What is a relative minimum?
300
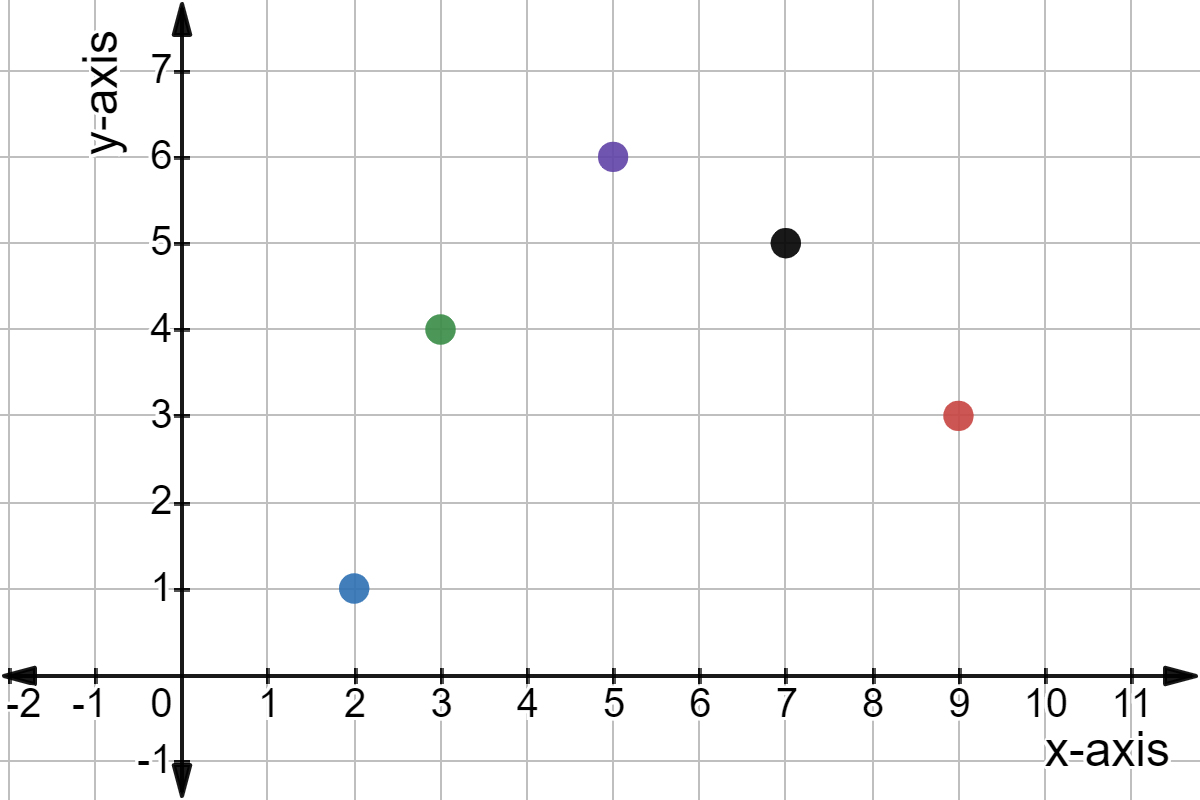
{2, 3, 5, 7}
What is the domain of the graph?
300
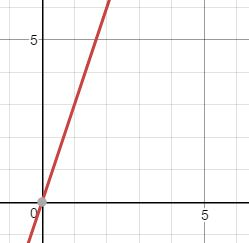The origin
What is the location of both the x and y intercepts?
300
The "word-fraction" we use to determine the slope and how we plot a line on a graph
What is rise over run?
300
The values of x that would make this equation true:
|x-3|=7
What is -4 and 10?
(x equals ten and x equals negative four)
400
We have this when a slope changes from positive to negative on a graph resulting in a high point
What is a relative maximum?
400
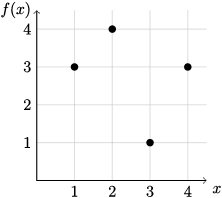
{1, 3, 4}
What is the range of the function?
400
The parent equation for all LINEar functions
What is y=x?
(y equals x)
400
The slope for the pictured graph
What is 3 or 3/1?
400
The location of the vertex on the following graph:
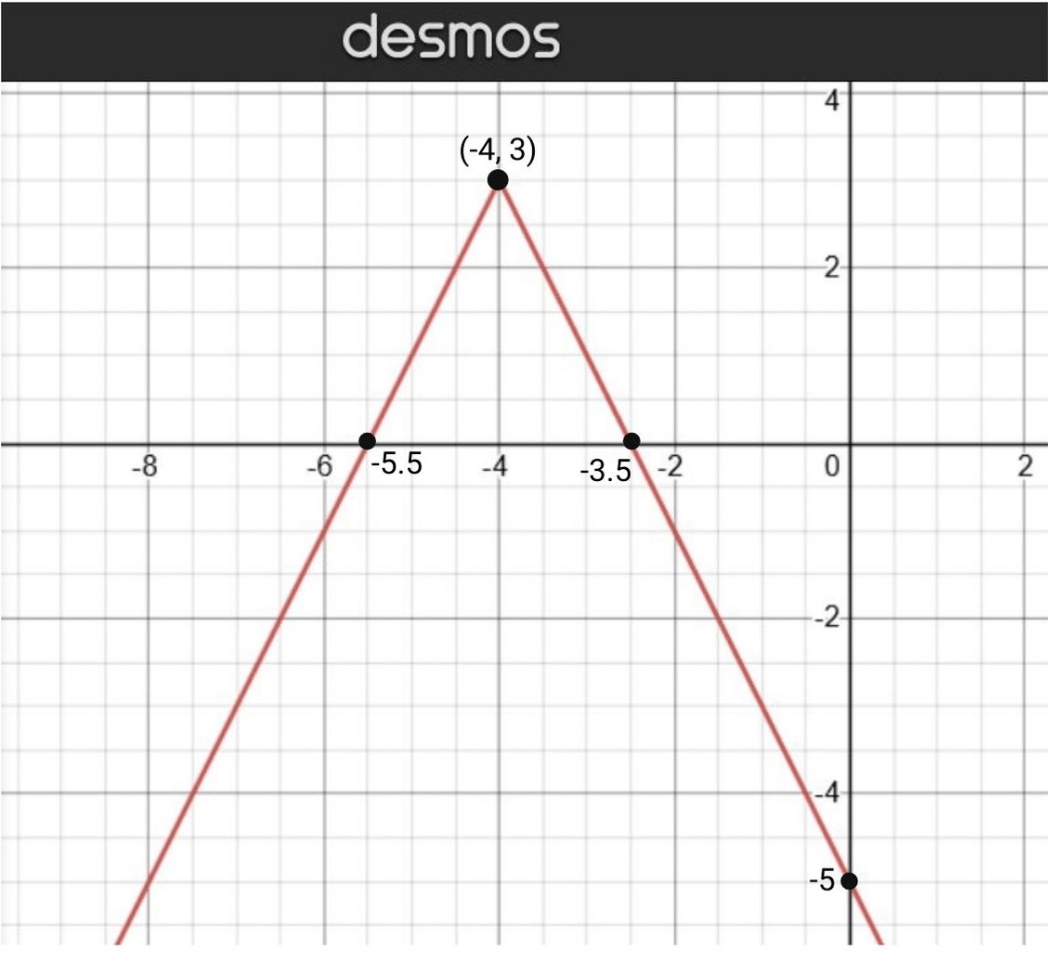
What is (-4, 3)?
(negative four three)
500
The form or naming system we use to label intervals of increasing and decreasing. It's a lot easier than inequality notation and looks like this: [0, 10)
What is interval notation?
500
The numbers that our function returns to us
What is the range?
500
To solve for this, we would take our linear equation and plug in 0 for y
What is the x-intercept?
500
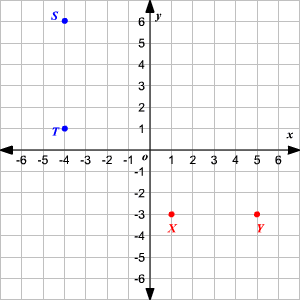
The letter associated with the coordinate (5, -3)
What is Y?
500
The term used for false solutions that do not work when plugged back into an absolute value equation
What are extraneous solutions?