Imaginary Numbers/Extra
Quadratics 1
Quadratics 2
Quadratics 3
100
What is the
sqrt(-96)
4isqrt6
100
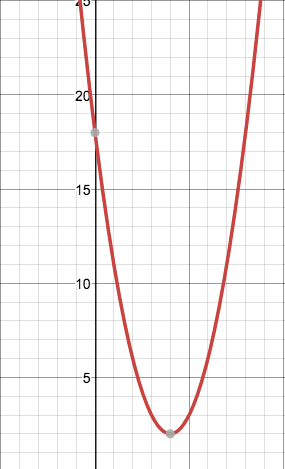
Graph the following:
x^2-8x+18
100
Factor the following:
x^2-2x-35
(x - 7)(x + 5)
100
Use the quadratic formula to solve the following quadratic formula:
4x^2+4x=7
-1/2+-sqrt2
200
Simplify
(6+3i)-(4-3i)
2+6i
200
Determine if there are any solutions and list them.
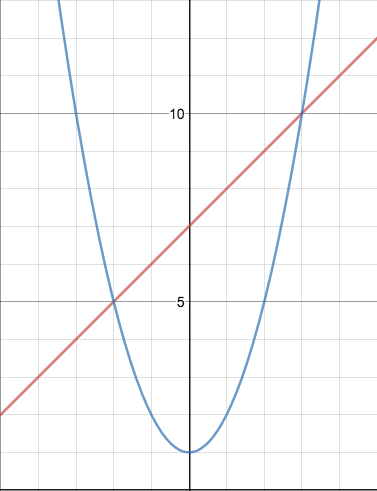
(-2, 5) and (3,10)
200
12x^2-15x-18
What is the factored form of the following:
(12x + 9)(x - 2)
200
Determine the nature of the solutions:
5x^2+6x+1
Two real, rational roots
300
Simplify
(4+5i)(2-i)
8-4i+10i-5i^2
8+6i+5
13+6i
300
Describe the transformation that occurs from f(x)=x^2 to
g(x)=(x+6)^2-4
6 left
4 down
300
Solve the following by factoring:
6x^2+5=11x
(6x - 5)(x - 1)
300
Write the equation using the given information:
focus: (4, 0); directrix: x = -4
x=1/16y^2
400
Solve for x:
4(x+7)^2+25=0
x=-7+-5/2i
400
Write the quadratic equation using the following information:
translate 3 left
vertical shrink by 0.5
translate 3 down
1/2x^2+3x+3/2
400
Use a number line to show the solutions of the following inequality:
2x^2-5x-12>=0
x>=4
x<=-3/2
400
Write the quadratic equation that passes through these three points:
(-3,2), (-1,0), (1,6)
y=x^2+3x+2
500
List as many digits of pi as your team can.
3.141592653
500
Rewrite the following in vertex form:
2x^2-16x+34
2(x-4)^2+2
500
Factor the following:
4x^2+9
(x+3/2i)(x-3/2i)
500
Identify the vertex, x/y-intercepts, and axis of symmetry of the following quadratic:
-3x^2+8x+16
vertex: (4/3, 64/3)
y-intercept: 16
x-intercepts: -4/3, 4
axis of symmetry: x=4/3