Solving Quadratics
Equations in Quadratic Form
Vertex Form
Graphing Parabolas
Word Problems
More Word Problems!
Discriminant
Graphing Polynomials using Graphing Calculator
100
y2-6y - 9 =0
3 ± 3√(2)
100
5a + 6√(a) + 1 = 0
No solution, 1/25 ext, 1 ext
100
Find the equation of the parabola with vertex (1, -2) passing through (2, 1).
y = 3(x-1)2 - 2
100
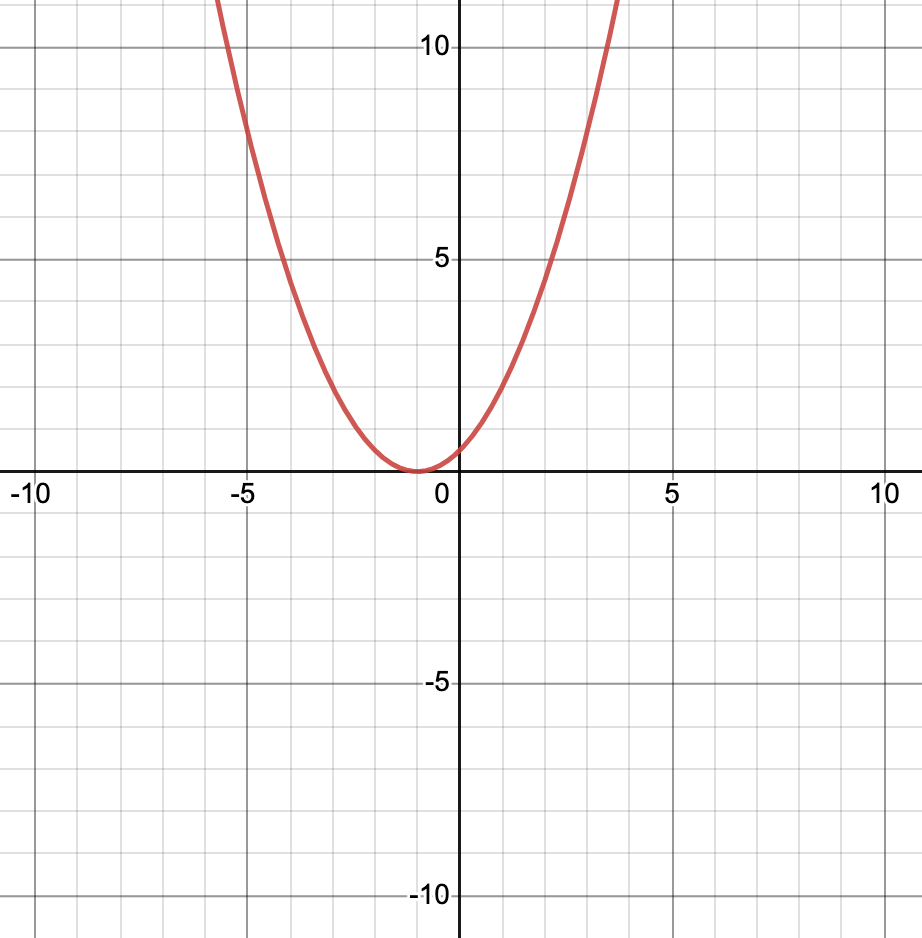
Graph the function using at least 5 points. Find the vertex, axis of symmetry, domain, range, and maximum/minimum. f(x) = 4-x2
V: (0, 4)
A.O.S.: x = 0
D: all real numbers
R: y ≤4
Max at 4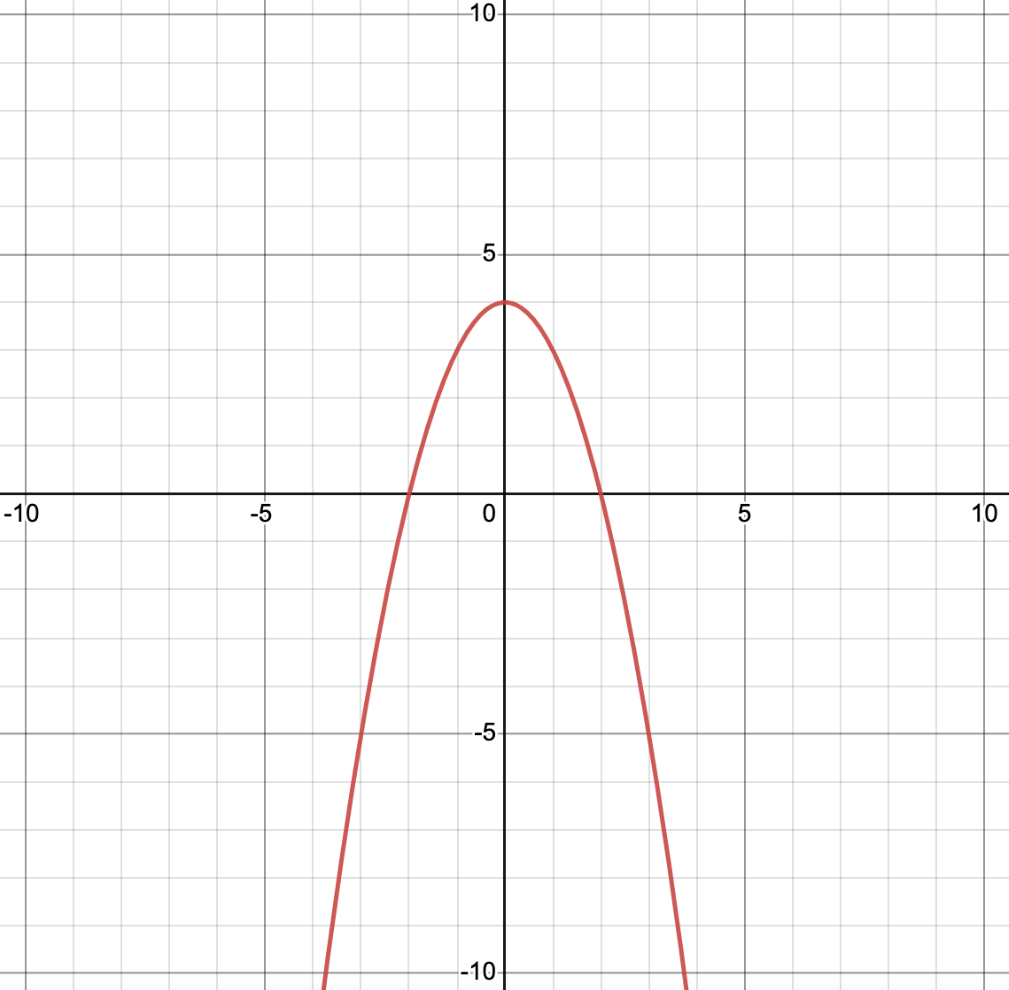
100
A vegetable garden measures 8ft by 12ft. If we increase each dimension by x ft, the area is doubled. What is x?
4ft
100
Find two numbers with a sum of -8 and a product of -209
11 and -19
100
Without solving, use the discriminant to determine the nature of the solutions.
x2+3x -9 = 0
The discriminant is 45 which means that there are 2 real irrational solutions because 45 is not a perfect square so we will get a radical in the answer.
100
Approximate the relative extrema, real zeros, and y-intercept of P(x) = x⁴-x³+x²-3x + 1 to the nearest hundredth. Use those points to make a graph. How many real zeros and how many complex zeros are there?
relative minima: (1, -1)
relative maxima: none
zeros: 0.37, 1.43
y-intercept: 1
2 real and 2 complex
200
2a2 + 6a + 7 = 2
-3/2 ± 1/2i
200
4x4 + 7x2-36 = 0
{3/2, -3/2, 2i, -2i}
200
Find the equation of the parabola with vertex (-2, 6) and has a y-intercept at -2.
y = -2(x+2)2 + 6
200
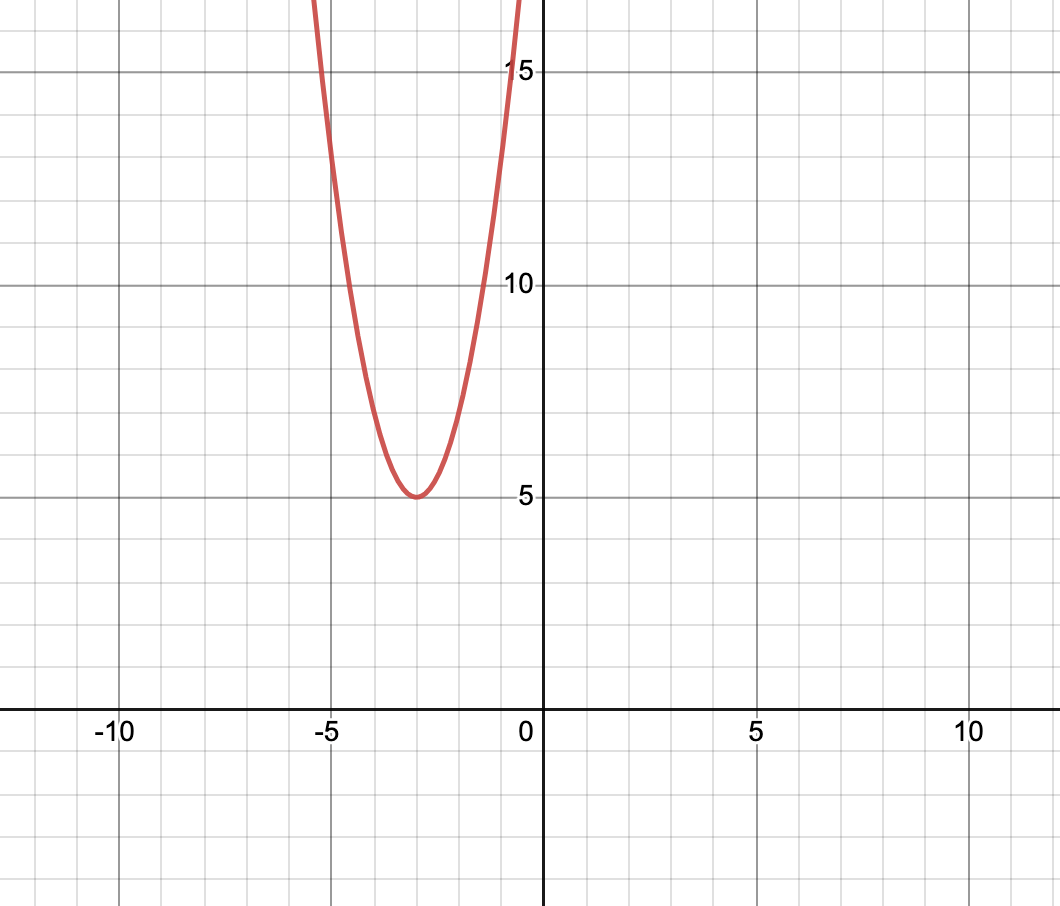
Graph the function using at least 5 points. Find the vertex, axis of symmetry, domain, range, and maximum/minimum. f(x) = 2(x+3)2+5
V: (-3, 5)
A.O.S.: x = -3
D: all real numbers
R: y ≥5
Min at 5
200
Find the dimensions of a rectangle whose perimeter is 10 cm and whose area is 3 cm2.
\frac{5 + \sqrt{13}}{2} \text{ by } \frac{5 -\sqrt{13}}{2}
200
Find the maximum height of the rocket if the initial vertical velocity is 64 ft/s and the initial height is 15 ft.
After 2 s, the rocket reaches a maximum of 79 ft.
200
Without solving, use the discriminant to determine the nature of the solutions.
x2 - 4x - 5= 0
The discriminant is 36 which means there are 2 real rational solutions because 36 is a perfect square so we won't get any radicals in the answer.
200
Approximate the relative extrema, real zeros, and y-intercept of P(x) =x4-3x3+x+5 to the nearest hundredth. Use those points to make a graph. How many real zeros and how many complex zeros are there?
relative minima: (2.20, -1.32), (-0.31, 4.79)
relative maxima: (0.36, 5.24)
zeros: 1.76, 2.54
y-intercept: 5
2 real and 2 complex
300
x2-2x = 4
1 ± √(5)
300
3(x2-2)2 -8(x2-2) + 4 = 0
{2, -2, 2/3√(6), -2/3√(6) }
300
Find the vertex and state whether it is a minimum or maximum: h(x) = (2x-5)(2x+3)
minimum; (1/2, -16)
300
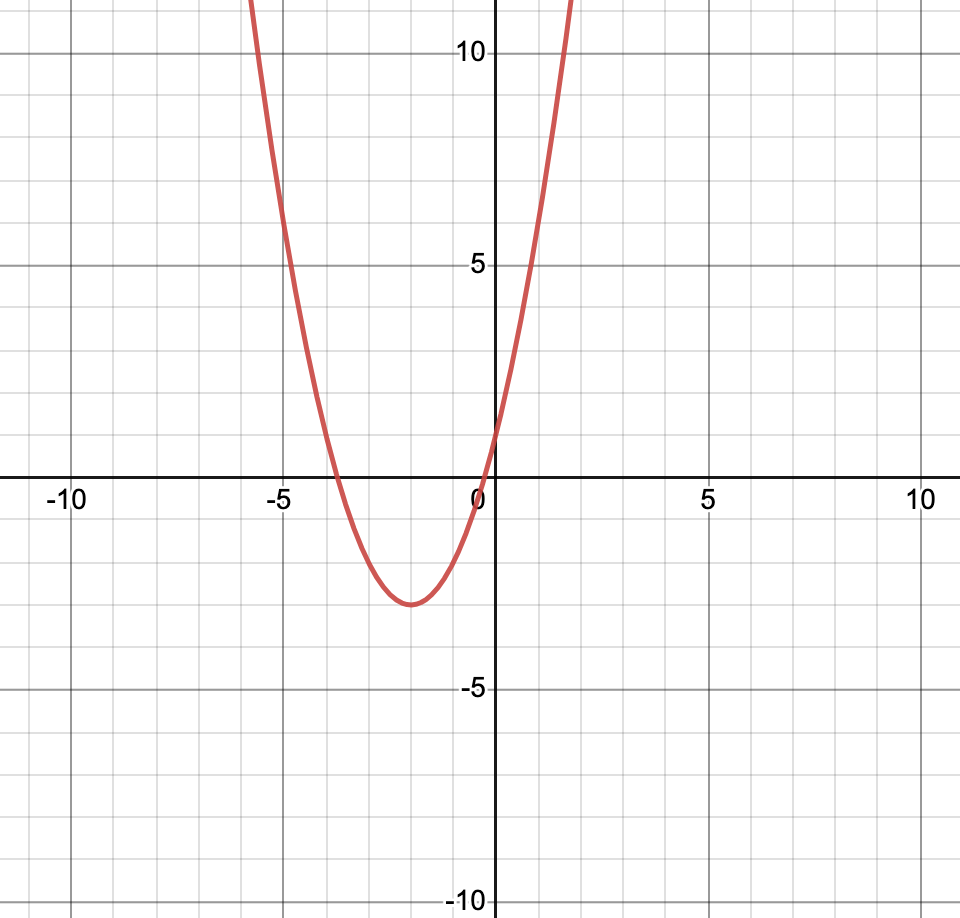
Graph the function using at least 5 points. Find the vertex, axis of symmetry, domain, range, and maximum/minimum. g(x) = x2+4x+1
V: (-2, -3)
A.O.S.: x = -2
D: all real numbers
R: y ≥-3
Min at -3
300
A walkway of uniform width has area 72 m2 and surrounds a swimming pool that is 8 m wide and 10 m long. Find the width of the walkway.
(3\sqrt{17} -9)/2
300
Lola throws a baseball into the air with an initial vertical velocity of 32 ft/s from a height of 5 ft. (a) How high will the ball go? (b) When will it hit the ground?
a) 21 ft
b)
1+ sqrt{21}/4 s
300
Without solving, use the discriminant to determine the nature of the solutions.
x2+8x +20 = 0
The discriminant is -16 which means that there will be 2 complex solutions because there is a negative in the radical so there will be an i in the answer.
400
4k2 + k + 1 = 0
-1/8 ± i√(15)/8
400
(x2-1)2 - 11(x2-1) = -24
{2, -2, 3, -3}
400
Put the function in vertex form, find the vertex, the domain, and the range: f(x) = 6x-3x2
f(x) = -3(x-1)2 +3
(1, 3)
D: { all real numbers}
R: { y | y ≤ 3}
400
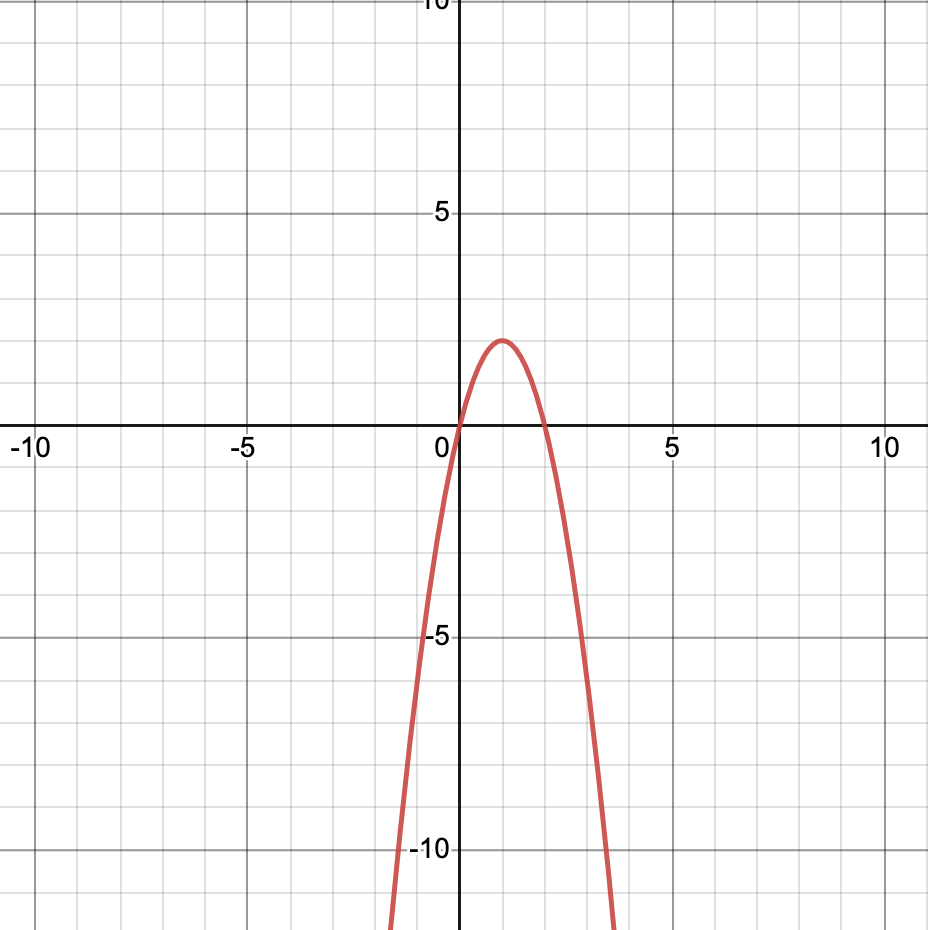
Graph the function using at least 5 points. Find the vertex, axis of symmetry, domain, range, and maximum/minimum. h(x) = 4x-2x2
V: (1, 2)
A.O.S.: x = 1
D: all real numbers
R: y ≤ 2
Max at 2
400
A positive real number is 1 more than its reciprocal. Find the number.
(\sqrt{5} + 1)/2
400
Eddie is organizing a charity tournament. He plans to charge a $20 entry fee for each of the 80 players. He recently decides to raise the entry fee by $5, and 5 fewer players entered with the increase. (a)How much should he charge in order to maximize the prize pool?(b)What is the maximum value of the pool?
a) $50
b)$2500
400
Without solving, use the discriminant to determine the nature of the solutions.
x2 + 4 = 4x
The discriminant is zero which means there is 1 real, rational double root because 0 is the only number with one square root.
500
z2 - (3+2i)z + (1+3i) = 0
2+i, 1+i
500
2/a + 1/√(a) = 1
{4}
500
Put the function in vertex form, find the vertex, the domain, and the range: f(x) = 2x2 - 10x +9
f(x) = 2(x-5/2)2-7/2
(5/2, -7/2)
D:{all real numbers}
R: {y | y ≥ -7/2}
500
Graph the function using at least 5 points. Find the vertex, axis of symmetry, domain, range, and maximum/minimum. g(x) = 1/2x2 + x + 1/2
V: (-1, 0)
A.O.S.: x = -1
D: all real numbers
R: y ≥ 0
Min at 0
500
A rectangular prism has side lengths x, 2x, and x+2. The surface area is 36 m2. What is x?
(3\sqrt{11}-3)/5
500
A bike rental shop rents an average of 120 bikes per week and charges $25 per day. The manager estimates that there will be 15 additional bikes rented for $1 reduction in the rental price. (a) Find the maximum income (b) what is the new price of a bike
$4083.75
$16.50/ day
500
Find the value of k for which the equation has a double root.
2x2 + 4x + k =0
k =2