Transformations Pt 1
Radical Equations
Rational Exponent Eq.
Inverses
Transformations Pt 2
100
What transformation is happening to the following equation?
g(x) = (x+4)3
Move to the left by 4
100
sqrt(x)=4
Solve the equation
x = 16
100
Solve the following equation
x^(2/3)=9
x = 27
100
Find the inverse of
f(x)=root(3)(2x)
f^(-1)(x)=1/2 x^3
100
Describe the transformations done to the graph
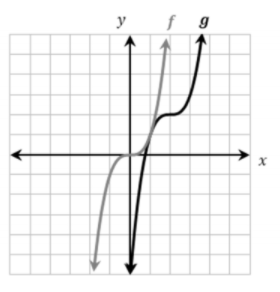
Moved right 2 and up 2
200
What transformation is happening to the graph?
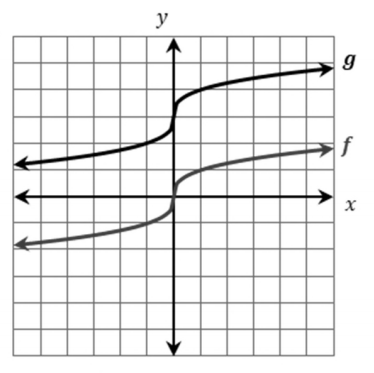
Moved up 3
200
root(3)(x-4)=3
Solve the equation
x = 31
200
Solve the following equation
5x^(1/4)=30
x = 1296
200
Find the inverse of
f(x)=sqrt(6x)
f^-1(x)=1/6x^2
200
Describe the transformations done to the graph
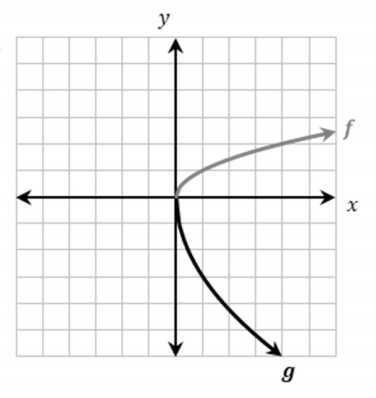
Reflection across x-axis and vertical stretch.
300
What transformation is happening to the equation?
sqrt(-x)
Reflection across the y-axis
300
Solve the following equation
4sqrt(x+5)=28
x = 44
300
Solve the following equation
3x^(2/5)+4=7
x = 1
300
Find the inverse of
f(x)=x^2+1 and x>=0
f^-1(x)=sqrt(x-1)
300
Describe the transformation done to the following equation.
g(x)=-root(3)((x-1))-3
Reflection across the x-axis
Moved right 1
Moved down 3
400
Describe the transformation that has happened to the graph below.
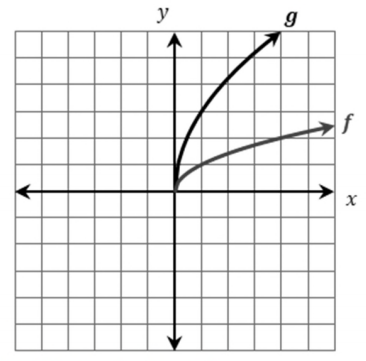
Vertical stretch by 3
400
Solve the following equation
root(3)(-x+6)=root(3)(10x-5)
x = 1
400
Solve the following equation
1/8 x^(4/3)=2
x = 8
400
Find the inverse of
f(x)=64x^3+3
f^-1(x)=root(3)((x-3)/64)
400
Write an equation for the following transformations done to f(x) = x3
Reflection across the y-axis, vertical compression by 1/3, and moved up 8
g(x)=1/3(-x)^3+8
500
Describe the transformation that has happened to the graph below (red is original).
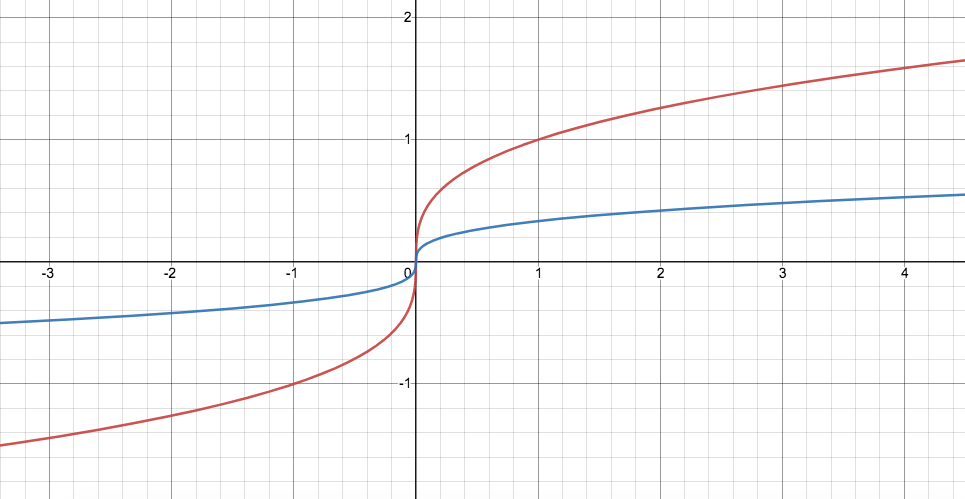
Vertical compression by 1/2
500
Solve the following equation
sqrt(x+56)=x
x = 8
500
Solve the following equation
3/2 (x+9)^(3/5)=12
x = 23
500
Determine if the following functions are inverses
f(x)=36x^2
g(x)=1/6sqrt(x)
Yes they are!
500
Write an equation that represents g on the graph
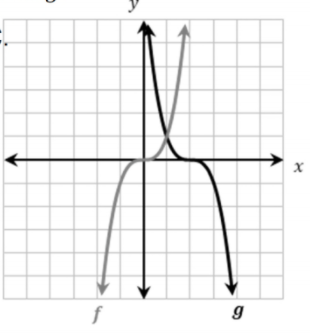
g(x)=-(x-2)^3