6a = 54
a = 9
10b - 3b =
10b - 3b = 7b
Expand 5(a + 6)
5(a + 6) = 5a + 30
Factorise 4a + 16
4a + 16 = 4(a + 4)
m = 4p + 1
x/7=4
x = 28
3a2 x 2b4 x a6
6a8b4
Expand -y(5 - 7y)
-y(5 - 7y) = -5y + 7y2
Factorise
16a2 + 8a
16a2 + 8a = 8a(2a +1)
y = 3x - 2
What is the gradient?
What is the y-intercept?
Gradient = 3
Y-intercept = -2
3x - 10 = -1
x = 3
(6x^3y^8)/(24x^5y^4)
y^4/(4x^2)
Expand 3a( 2 - 4a3)
3a( 2 - 4a3) = 6a - 12a4
Factorise
10x + 40y + 60z
10x + 40y + 60z = 10(x + 4y + 6z)
What is the rule for this pattern?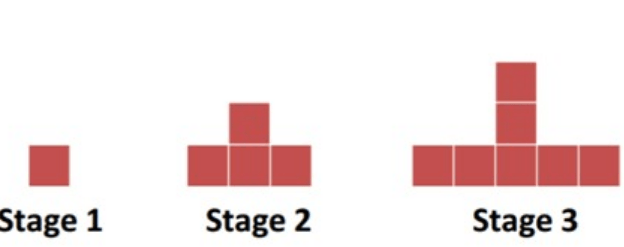
3n -2
-2(3 - x) = 10
x = 8
-7x2 + 5x - 7x + 10x2
3x2 - 2x
Expand
(x + 2)(x + 3)
(x + 2)(x + 3) = x2 + 5x + 6
x2 + 3x + 2
x2 + 3x + 2 = (x + 1)(x+2)
What is the rule for this pattern?
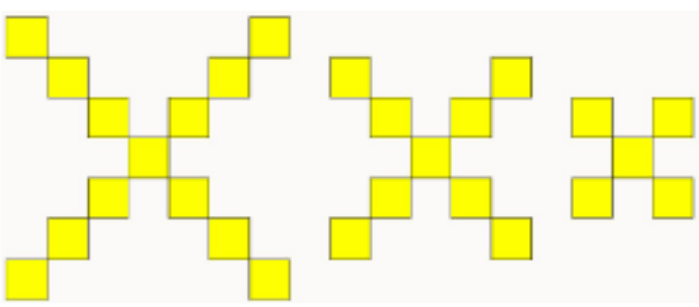
-4n +17
5x - 10 = - 4x +8
x = 2
((2x^3)^2)/(4x^2y^3)
(x^4)/(y^3)
Expand
(x - 4)(x + 8)
(x - 4)(x + 8) = x2 + 4x - 32
Factorise
x2 - 9x -10
x2 - 9x -10 = (x + 1)(x - 10)
What is the equation of this line?
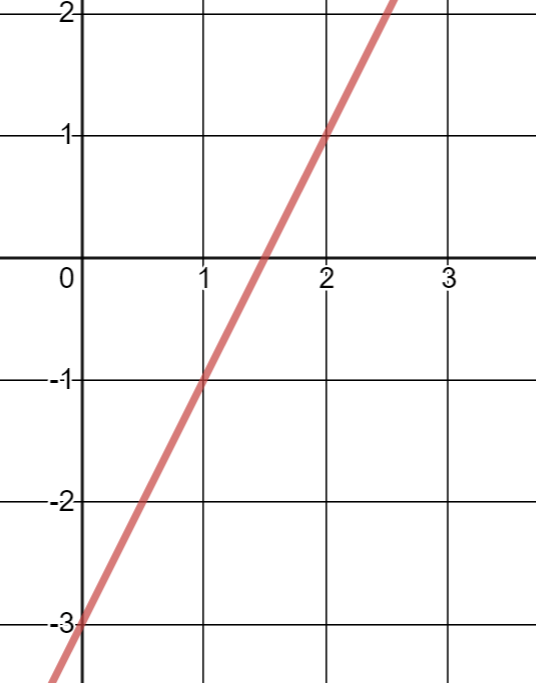
y = 2x -3