Algebra and Pre-Algebra Review

Vocabulary

Systems

Add & Subtract

Multiplicationation & Division

Grab Bag Part 1

Grab Bag Part 2

100

Is 2d + 5 an expression or an equation?

Expression

100

PA: Convert 120 ft = _________yd

Alg: Solve the following systems of equations using substitution:

x = 6

y = 2x - 3

40 yd

(6,9)

100

What are the "like" terms in the expression 6h + 5y - 2y +8

5y and -2y

100

What is the slope of the graph of: y=12x−19?

100

Convert 250.25 to a mixed number.

250 1/4

100

(0.15)(0.5)

0.075

150

Is 5c - 2c = 3c and expression or equation?

Equation

150

How many solutions does the graph have?

1 solution

150

How many solutions does the graph have?

Infinite solutions

150

18 - 4k = -10 - 4k

No solution, null set

150

Algebra:

1. Find the total price of a sweatshirt that is priced at $48 and taxed at 6.5%.

2. Solve 5x - 3y = 9 for y.

Pre-Algebra:

1. (-3) + (-7)

2. -4 +11

3. 7-(-5)

4. 13 + (-2)+ (-9)

Algebra:

1. $51.12

2. y = 5/3x - 3

Pre-Algebra:

1. -10

2. 7

3. 12

4. 2

150

Reduce to lowest terms:

45/75

3/5

200

Which number is the coefficient in the equation 3x + 6 = 18

200

PA: Convert 3/4 mi. = _________ ft

Alg: How many solutions does the graph have?

PA: 3,960 ft

Alg: No solution

200

Evaluate

x^3 – xy – x/y if x = 2 and y = 1

200

1821.5/0.7

2,602.142857

200

Algebra:

1. On a map of North Carolina, the distance between Charlote and Wilmington is 14.75 in. If 2 in equals 24 miles, what is the approximate distance between the two cities?

2. Shanee bikes 5 miles to the park in 30 min and 3 miles to the library in 45 min. What is her average speed?

Pre-Algebra:

1. Evaluate: − 6 + 3(9 - 7)

2. Evaluate: −8 ÷ 8 (1 + 3) - 1

Algebra:

1. 177 mi

2. 6.4 mph

Pre-Algebra:

1. 0

2. -3

200

Solve for x : 3(x + 1) = -6

-3

250

Algebra:

1. A graph in which 2 sets of data are plotted as ordered pairs in a coordinate plane are called a __________.

Pre-Algebra:

1. Addition and subtraction are examples of _________.

Algebra:

1. scatter plot

Pre-Algebra:

1. Inverse operations

250

PA: You spend $40 on 5 pounds of concrete. What is the unit rate in dollars per pound?

Alg: Solve the following systems of equations using substitution:

5x - 2y = 3

y = 2x

$8 per pound

(3, 6)

250

(x+5)/4=7

Solve for x

x = 23

250

Simplify:

x + 10 -6(x - 3x) + 4

13x + 14

250

The number of red frogs exceeded the number of blue frogs by 80. The number of green frogs was 20 less than the number of blue frogs. If there were 120 blue fogs, what was the sum of the reds, the blues, and the greens?

420 frogs

250

9876.5 – 643.99

9,232.51

300

Write the following sentence as an equation:

Twice a number is 18 more than 5 times a number.

2x = 18 + 5x

300

PA: Will spent $3.75 for 3 pounds of granola. What is his unit rate in dollars per pound?

Alg: Solve the following systems of equations using substitution:

y = 3 - x

3y + x = 5

$1.25 per pound

(2,1)

300

Algebra:

Subtract the polynomials: (9x²-4x+11) - (3x²-2x+2)

Pre-Algebra:

How long would it take a car traveling 60 miles per hour to go 240 miles?

Algebra:

6x²-2x+9

Pre-Algebra:

4 hrs

300

Solve for k:

4(−2k−8)=6(k+18)

k = -10

300

For 4 hours Sam traveled at 40 miles per hour. Then he increased his speed to 60 miles per hour and drove for another 3 hours. How far did he go in the 7 hours he traveled?

340 mi

300

If 200 is increased by 130 percent, what is the resulting number?

460

350

Simplify: 3y - 9 if y = 3

350

Solve:
y=8x+1
y=6x+3

( 1, 9 )

350

15f−23=2(4f+20)

f = 9

350

Algebra:

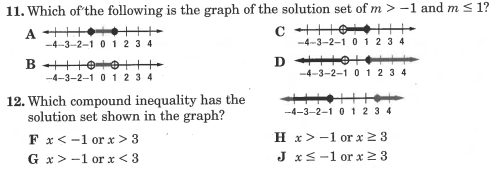
Pre-Algebra:

Algebra:

11. C

12. J

Pre-Algebra:

10. J

11. A

350

The first flock contained 5283 birds. The second flock contained 5 times as many birds. The third flock had twice as many birds as the second flock. How many birds were there in all?

84,528 birds

350

The whole batch cost $28,000 and contained 140 items. Write the two rates (ratios) implied by this statement. What would be the price for 200 items?

$40,000

400

The slope- intercept form of a linear equation is ___________.

1. y=mx+b

400

Alg:

Infinite solutions

400

There are 4 milk chocolates to every 2 dark in a box of chocolates. There are 34 dark chocolates in the box. How many milk chocolates are in the box?

400

Find the slope of the line passing through EACH pair of points.

1. (2,5) and (3,6)

2. (6,4) and (3,7)

1. 1

2. -1

400

Six times a number is 45 greater than the product of the number and -3. Find the number.

400

The ratio of roses to snapdragons was 4 to 5. If there were 26,000 roses on the float, how many snapdragons were there?

32,500

500

Algebra: Find the x-intercept and y-intercept of the following equations:

2x - 3y = 24

X-int=12

Y-int = -8

500

What is the solution to this system?

2x + 3y = 4
y= 5x - 27

(5,-2)

500

Algebra:

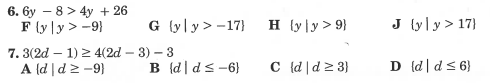
Pre-Algebra:

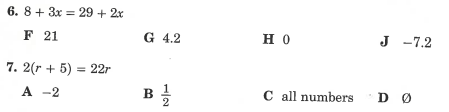
Algebra:

6. J

7. D

Pre-Algebra:

6. F

7. B

500

9 2/14 – 3 15/21

5 3/7

500

Algebra:

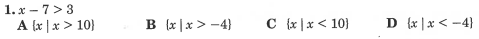
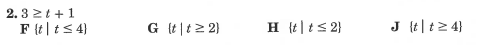
Pre-Algebra:

Algebra:

1. A

2. H

Pre-Algebra:

1. B

2. G

500

3 1/ 2 × 6 1/ 3 ÷ 2 1/3 × 1 1/ 3

38/3