Linear Equations and Inequalities
Systems
Graphs
Quadratics
Misc.
100
Solve the following equation:
-2 (r - 6) = -5 (-9r + 7)
x=1
100
Confirm the solution to the following system:
-x+6=-2y
3x=2-2y
(2, -2)?
Yes, (2, -2) is a solution
100
Write an equation for the following graph in slope-intercept form:
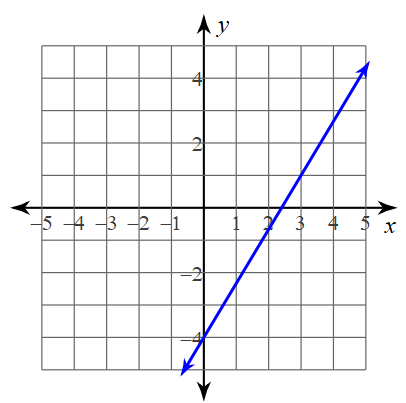
y=5/3x-4
100
Factor: 4x^2 -9
(2x+3)(2x-3)
100
Simplify. Your answer should contain only positive exponents.
2 x^0y^-3*4x^3y^-3
(8x^3)/y^6
200
Solve the following inequality and graph the solution:
-6(n+7)+3> -81
n<7
200
Solve the system by graphing:
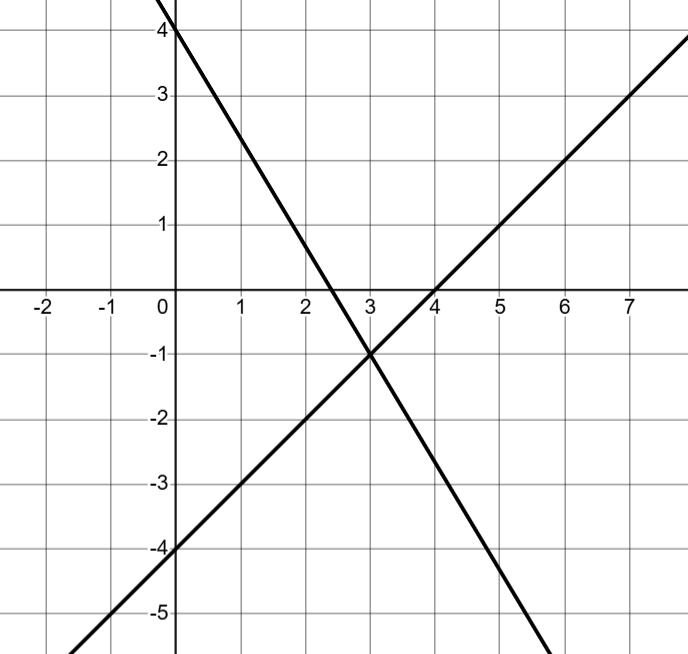
(3, -1)
200
Write the linear inequality for the following graph:
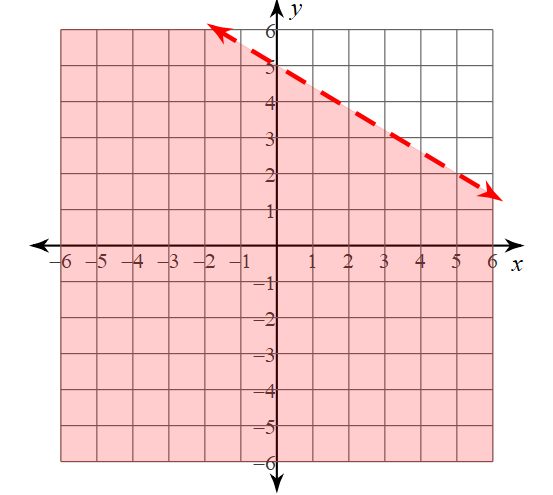
y< -3/5 x+5
200
Factor: x^2-7x+10
(x-5)(x-2)
200
Solve the following by taking the square root:
4(2x-2)^2 =16
x=0, 2
300
Solve each compound inequality and graph its solution:
-32<=7x-4<10
-4<=x<2
300
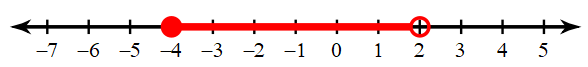
Write a system to represent the situation:
"Kali's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 7 adult tickets and 11 student tickets for a total of $116. The school took in $96 on the second day by selling 14 adult tickets and 5 student tickets. Find the price of an adult ticket and the price of a student ticket."
7a+11s=116
14a+5s=96
300
Identify the axis of symmetry from the graph. Confirm by completing the formula to calculate the AOS.
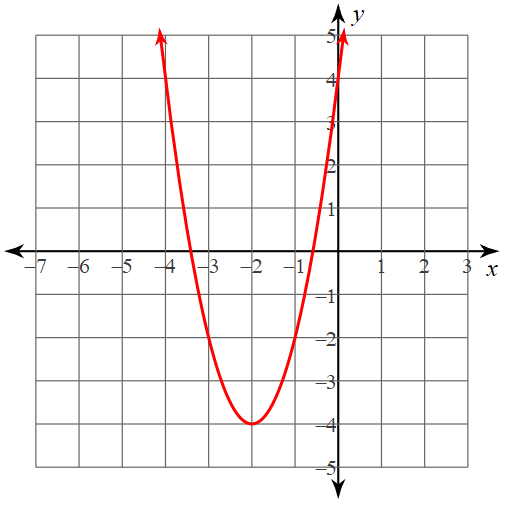
y=2x^2+8x+4
x=-2
300
Factor: 2x^2+3x-14
(2x+7)(x-2)
300
Simplify. Your answer should contain only positive exponents.
((2u^-1)^0)/(2u^3*u^2v^-1)
v/(2u^5)
400
Evaluate:
f(x)=-x^2 +4x
f(5)=
f(5)=-5
400
Solve the following system by substitution:
2x-2y=12
y=5x-14
(2, -4)
400
Find the domain and range.
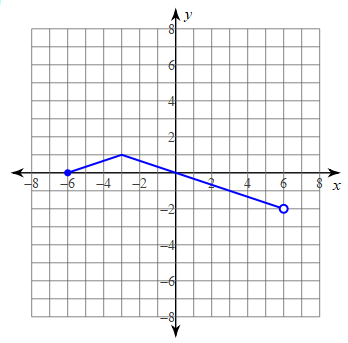
-6<=x<6
-2<y<=1
400
Solve by factoring:
p^2 -7p=-12
x=3, 4
400
Describe the transformation of f(x)=x^2 to create the graph:
g(x)=-2(x-4)^2 +5
- Reflection
- Stretch by 2
- Up 5
- Right 4
500
Evaluate:
f(x)=3x-6
f(x)=-3, x=
x=1
500
Solve the system by elimination:
-14x+8y=-4
-7x+4y=-2
Infinitely Many Solutions
500
Write the equation of the parabola in vertex form:
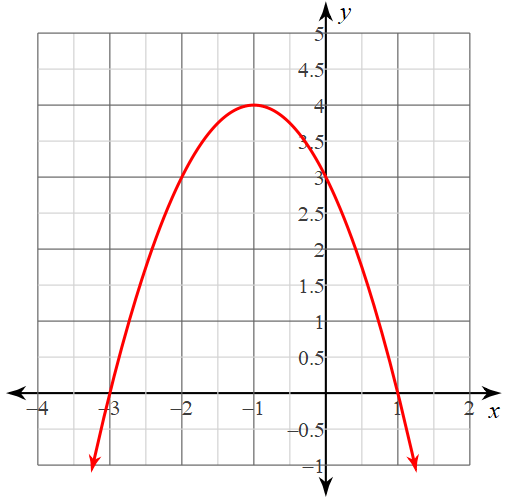
y=-(x+1)^2 +4
500
Solve using the quadratic formula:
7x^2+3n-8=0
x=(-3+- sqrt(233))/14
500
Solve the following quadratic by Completing the Square:
x^2 +8x=-13
x=-4+-sqrt(3)