Grinch
Mistletoe
Elf
Gingerbread
Jolly
100
Determine if the ordered pair (-5, -1) is a solution of 2x – y = -11.
Not a solution
100
Solve the equation.
-3 – 5x = 47
x = -10
100
A fellow student graphs the system
y = -2x + 3
y = -2x +1
and finds that the lines are parallel. What does this indicate about the system of equations?
There is no solution.
100
Solve the inequality.
x – 11 > -2x + 1
x > 4
100
A bakery sells cookies (x) for $1.50 each and muffins (y) for $2.50 each. A customer buys at least 5 items, and spends no more than $15. The system of inequalities to model this situation is
1.5x + 2.5y ≤ 15
x + y ≥ 5
Can a customer buy 4 cookies and 5 muffins? Why or why not?
No, it will cost too much money.
200
Simplify.
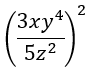
9x2y8/25z4
200
Marty is spending money at the average rate of $3 per day. After 14 days he has $68 left. The amount left depends on the number of days that have passed. Write an equation to model the situation.
y-68 = -3(x -14)
200
Simplify.
7y3∙10x3y5∙8xy3
560y11x4
200
Graph the inequality.
5x – 3y ≤ -15
Teacher looks at graphs
200
Graph the equation below.
y + 3 = -2(x – 2)
Teacher looks at graphs
300
Your study partner chooses to solve the system
2x – y = 4
3x + 2y = 8
by elimination. What is a potential challenge they might face when using the elimination method for this system?
A) It requires graphing skills
B) There may be extra steps to eliminate a variable
C) It is not suitable for systems with two equations
D) The solution may not exist
B
300
Find the slope.
(1, 3) and (-2, 0)
1
300
In the inequality 3x + 2y < 6, select all ordered pairs that are solutions.
A) (1, 1)
B) (2, 0)
C) (-1, 4)
D) (0, 3)
A and C
300
A rectangular garden is 8 feet longer than it is wide. If the perimeter of the garden is 40 feet, find the dimensions of the garden. Be sure to write an equation to model this situation.
Equation: 4x + 16 =40
Solution: width is 6, length is 14
300
Write an equation in slope-intercept form from the table.
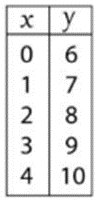
y = x + 6