Linear Equations
System of Equations
Arithmetic & Geometric Sequences
Radicals
Quadratic Equations
System of Linear & Quadratic Equations
100
Write an equation in slope intercept form that goes through the following two points?
y = 14x - 62
100
The state fair is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 8 vans and 8 buses with 240 students. High School B rented and filled 4 vans and 1 bus with 54 students. Every van had the same number of students in it as did the buses. Define the variables and write the system that represents the situation.
v = vans
b = buses
8v + 8b = 240
4v + b = 54
100
What is the formula for Arithmetic Sequence?
an = a1 + d(n - 1)
100
sqrt6/sqrt7
sqrt42/7
100
Solve the following quadratic equation via factoring:
x^2-24x+144=0
x = 2
100
What is the solutions of the system?
y=x^2-4x+4
y=x-2
Solutions: Two Real Solutions
(2, 0) and (3, 1)
200
Write an equation of a line that is parallel to the following equation and point.
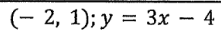
y = 3x + 7
200
Define the variables and write a system that represents the situation.
x = salad
y = lemonade
3s + 2l = 14
2s + 4l = 12
200
What is the formula for Geometric Sequence?
200
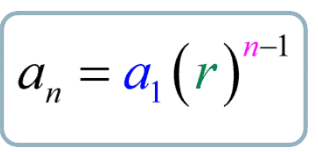
sqrt(24x^7) * sqrt(30x^6)
12x^6sqrt(5x)
200
Solve the following Quadratic Equation via factoring:
5x^2-19x=-18
t = 9/5 and t=2
200
What is the solution to the following system?
y=-(x+2)^2+5
y=5
One Real Solution: (-2, 5)
300
Write an equation of a line that is perpendicular to the following equation and point.
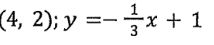
y = 3x - 10
300
Solve the following system of equations using either substitution or elimination.
3s + 2l = 14
2s + 4l = 12
s = 4
l = 1
300
What is the formula to find the sum of the terms in an Arithmetic Sequence?
300
3sqrt(18x) + 2sqrt(5x)
9sqrt(2x)+2sqrt(5x)
300
Solve the following equation via the quadratic equation:
2x^2+x=5
x= (-1+-sqrt41)/4
300
What is the solution to the the following system?
y=x^2-2x+4
y=x-1
No Solution
400
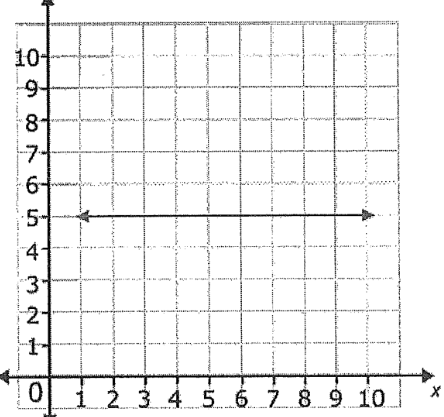
What is the slope of the following line.
Zero
400
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Define the variables and write the system.
Variables:
x = senior citizen
y = child
3x + y = 38
3x + 2y = 52
400
Firewood is stacked in a pile. The top row has 14 logs. There are 7 rows of logs. Each row has 2 more logs than the previous row. How many logs are there in all?
224 logs total
400
-4sqrt(28x) * sqrt(7x^3)
-56x^2
400
Solve the following Quadratic Equation using the Quadratic Formula:
5x^2+10x+7=0
No Solution
400
What is the solution to the following system?
y=-x^2+2x+7
y=-2x+2
Two Real Solutions:
(5, -8) and (-1, 4)
500
What is the slope of the following line?
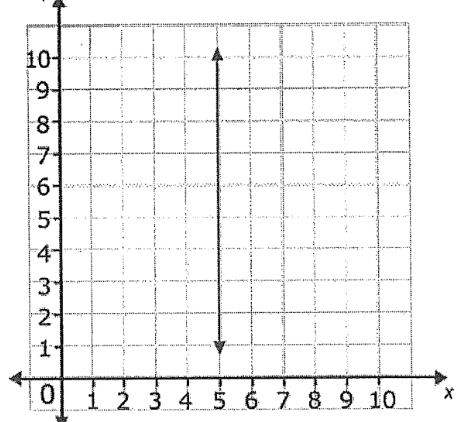
Undefined
500
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Solve the following system to figure out the cost of 1 senior citizen ticket and 1 child ticket.
3x + y = 38
3x + 2y = 52
senior citizen ticket: $8
child ticket: $14
500
Find the 12th number in the Geometric Sequence: 16, 12, 9, 27/4
*Make sure you leave your final answer as a simplified fraction.
177147/262144
500
sqrt(18a^3) * 4sqrt(3a^2)
12a^2sqrt6
500
Use either factoring or the Quadratic Formula to solve the following Quadratic Equation.
4y^2-4y-3=0
x=-1/2 and x=3/2
500
The path of a firework is described by the function:
h(t)=-4.9(t-5)^2+124
where h(t) is the height of the firework, in meters, and t is the time in seconds since launch.
a. What is the maximum height of the firework?
b. How many seconds does it take for the firework to reach the maximum height?
c. Use the quadratic formula to solve for how long the firework is in the air. (Round final answer to the nearest unit.)
a. 124 meters
b. 5 seconds
c. 10 seconds