Chapter 1
Chapter 2
Chapter 3
Chapter 4
Random
100
Solve the equation for x.
3(2x - 1) + 4x = 3
x = 3/5
100
Is the graph a FUNCTION or NOT A FUNCTION.
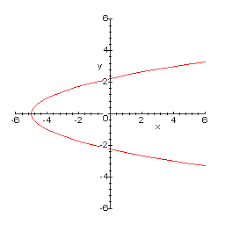
Not a function
100
Determine the axis of symmetry for the function
f(x) = -3x2 - 12x - 4
x = -2
100
Determine the degree and leading coefficient of the polynomial
f(x) = 3x2 - x4 + 9x - 3x6 + x3
Degree: 6
Leading Coefficient: -3
100
Draw the first 6 rows of Pascals Triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
200
Find the slope of the line that passes through the points
(2, 0) and (4, 6).
m = 3
200
Is the function a LINEAR FUNCTION or NOT A LINEAR FUNCTION?
y = sqrt(x) - 3
Not a linear function
200
Simplify.
sqrt(84)
2sqrt(21)
200
Multiply and simplify.
(x - 2)(2x3 - 3x2 - 6x + 2)
2x4 - 7x3 + 14x - 4
200
Name 3 factoring techniques/methods.
Reverse FOIL, GCF, Sum of 2 Cubes, Difference of 2 Cubes, Difference of 2 Squares, Grouping, etc.
300
In an inequality, what do you have to do if you divide both sides by a negative number?
Flip the inequality sign.
300
Find the x-intercept and y-intercept of the function.
y = -3x - 9
x-intercept: x = -3
y-intercept: y = -9
300
Multiply and simplify.
(-3 - 4i)(-2 - 6i)
-18 + 26i
300
Use synthetic substitution to find f(-4) for
f(x) = 2x3 + 6x2 - 7x + 20
f(-4) = 16
300
i4 = ?
1
400
Solve the system of linear equations using substitution or elimination.
x + 2y = 6
2x - 8y = 24
(8, -1)
400
Draw a graph with the following end behavior:
as x approaches positive infinity, f(x) approaches negative infinity
as x approaches negative infinity, f(x) approaches positive infinity
Answers vary.
400
Use the quadratic formula to find the zeros of the following function.
f(x) = 4x2 - 24x + 27
x = 3/2
x = 9/2
400
Factor by grouping.
f(x) = x3 + 2x2 - 3x - 6
f(x) = (x2 - 3)(x + 2)
400
What is Mr. Shult's favorite Christmas movie?
The Santa Clause