Which letters represent the Square Root Function?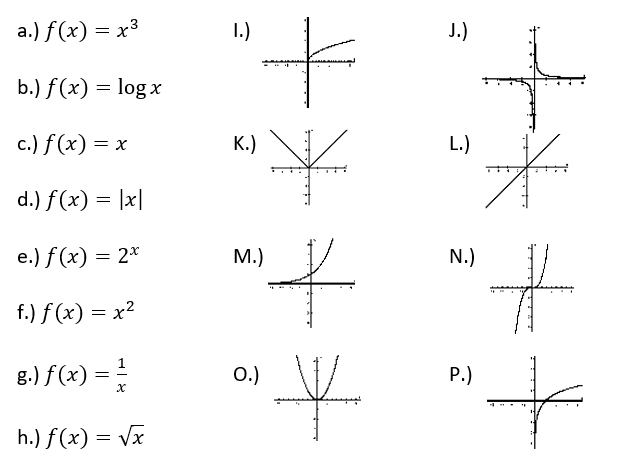
H & I
Which letters represent the Cubic Function?
A & N
Write a function g(x) for the given transformation of f(x)=x.
Reflected Down (x-axis) & Translated Up 6
g(x) = -x + 6
What transforms f(x) = x3 - 4 to g(x) = 3(x+2)3 - 7?
Vertically Stretched by 3
Translated Left 2
Translated Down 3
Evaluate the following piecewise function for f(3).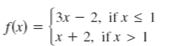
f(3) = 5
Graph the following piecewise function.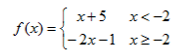
Which letters represent the Exponential Function?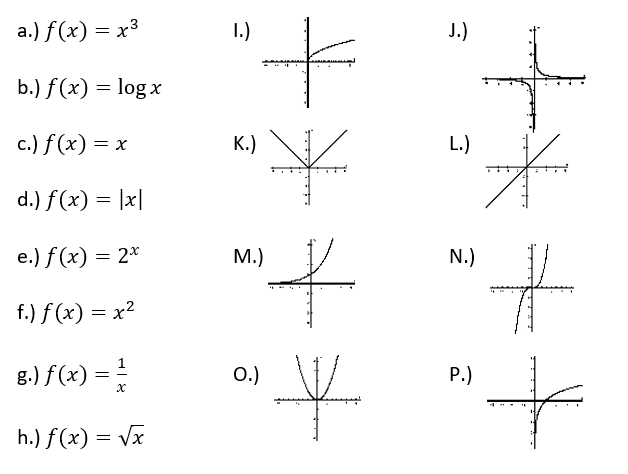
E & M
Which letters represent the Absolute Value Function?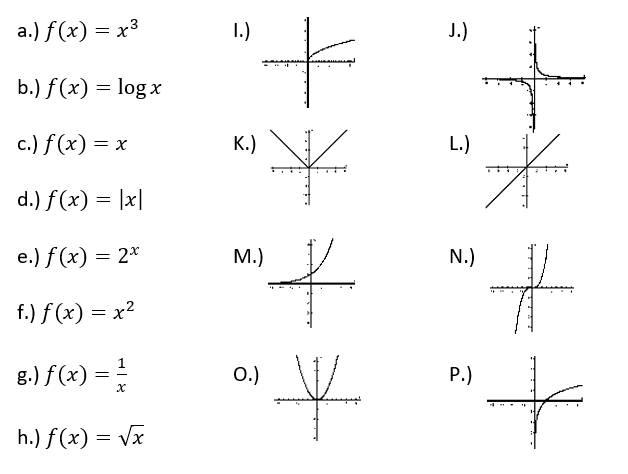
D & K
Write a function for the given transformation of f(x)=x2.
Vertically Compressed by 1/4 Translated Right 2
g(x)=1/4(x-2)^2
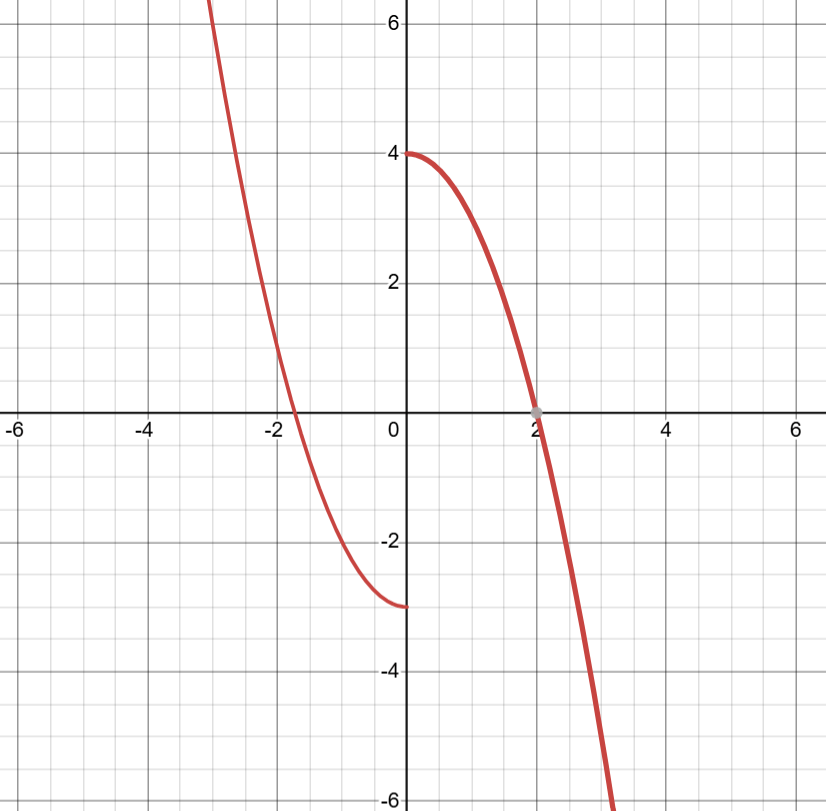
Write the translated function from the parent function from the graph.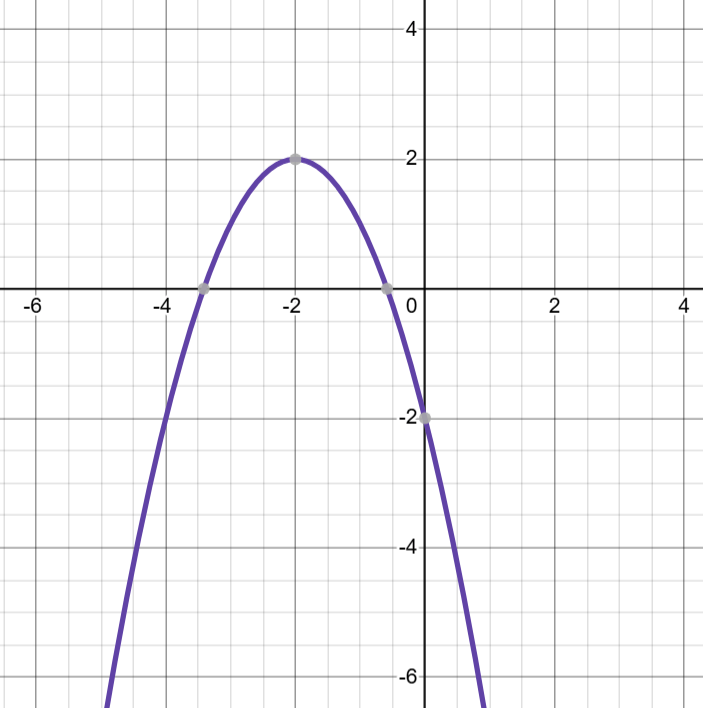
f(x)=-(x+2)^2+2
Evaluate the following piecewise function for f(-2).
f(-2) = -8
Graph the following piecewise function.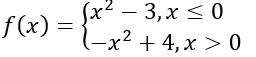
Which letters represent a Linear Function?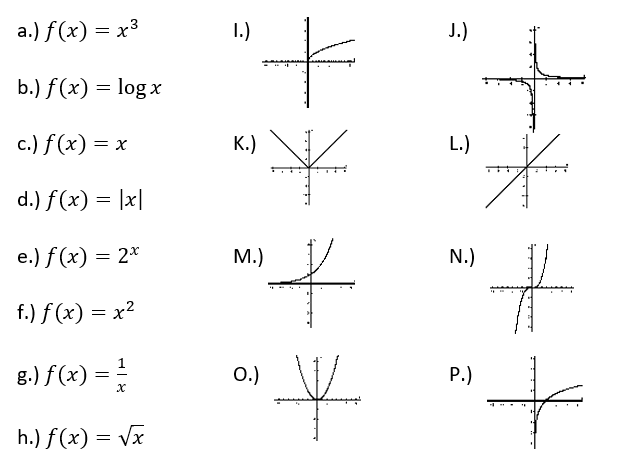
C & L
Which letters represent the Logarithmic Function?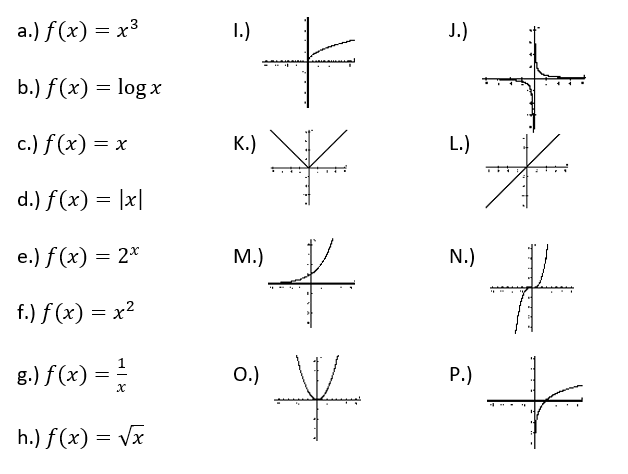
B & P
Vertically stretch the following function by 4 and shift it left 3. Call it g(x).
f(x)=sqrt(x+5)
g(x)=4sqrt(x+8)
Write the translated function from the parent function from the graph.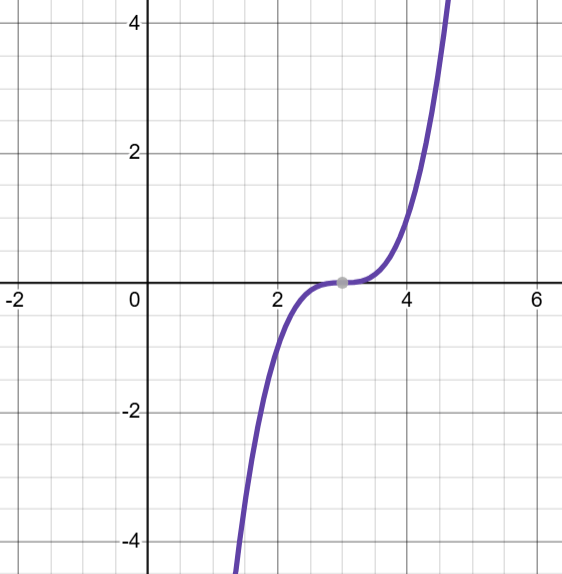
f(x)=(x-3)^3
Evaluate the following piecewise function for f(-4).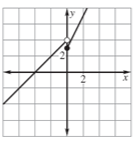
f(-4) = 0
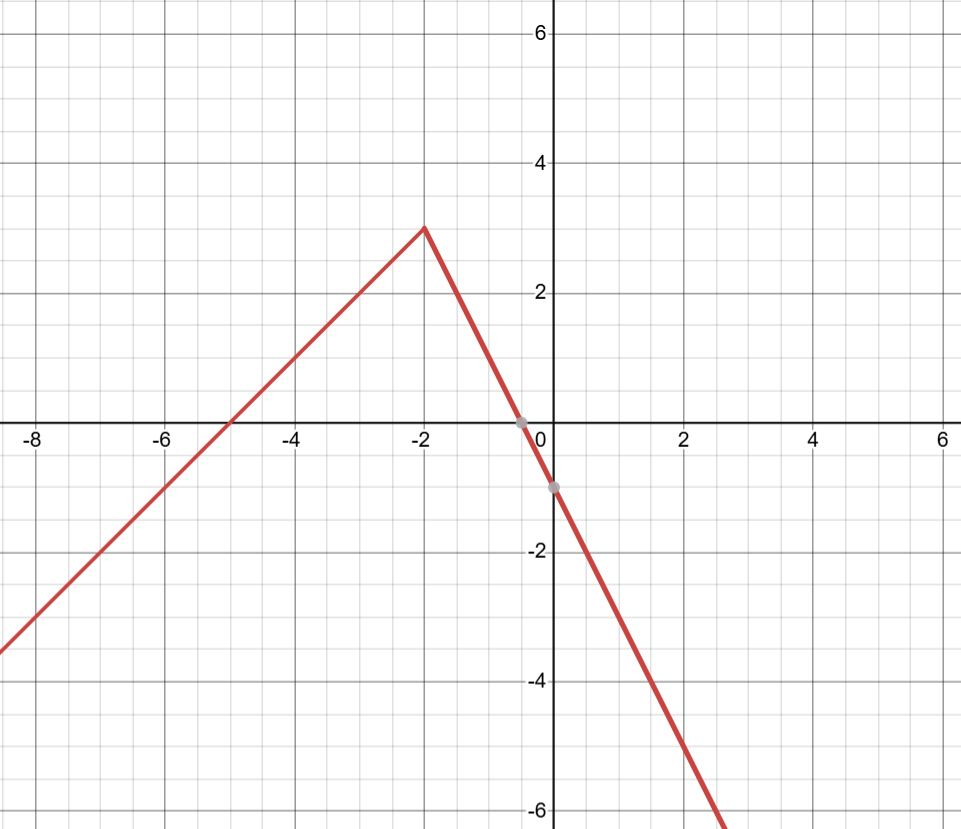
Write the piecewise function from the graph.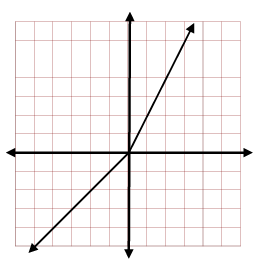
f(x) = x , x < 0
f(x) = 2x , x >= 0
Which letters represent the Rational Function?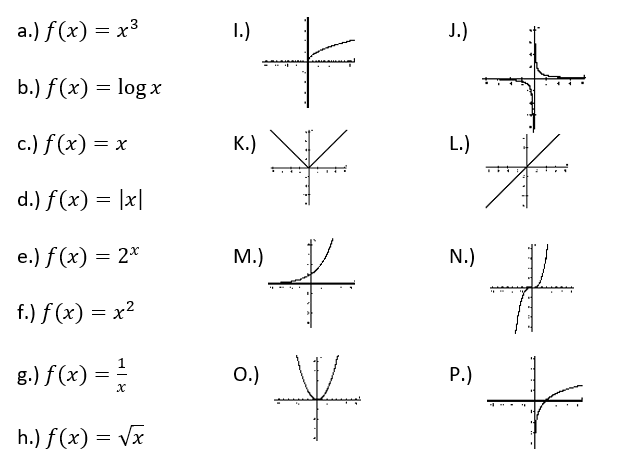
G & J
Which letters represent the Quadratic Function?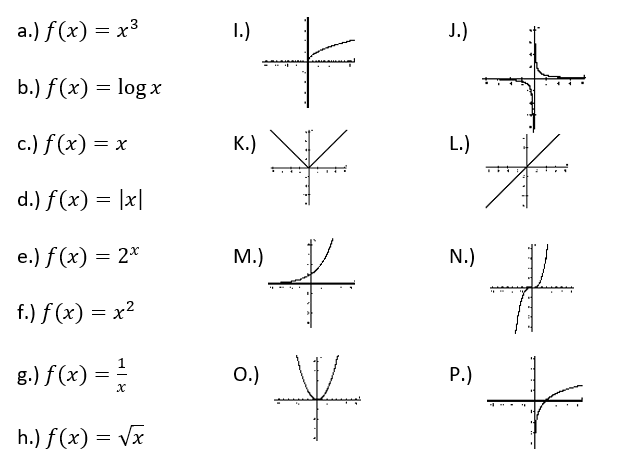
F & O
Reflect the following function across the y-axis and horizontally compress it by 1/5. Call it g(x).
f(x)=x^2-3
g(x)=(-5x)^2-3
State the domain and range of the graph below.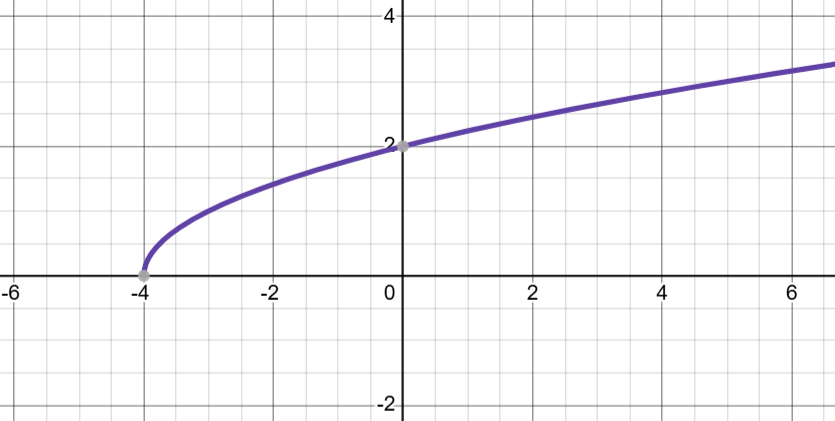
Domain: [-4, infinity)
Range: [0, infinity)
Evaluate the following piecewise function for f(1).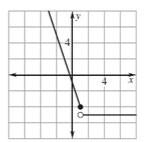
f(1) = -4
Write the piecewise function from the graph.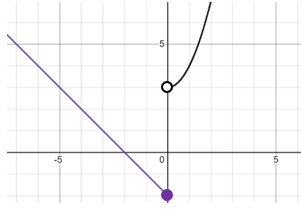
f(x) = x2+3 , x > 0
f(x) = -x-2 , x <= 0