Linear and Quadratics
Higher Order Polynomials
Rational Exponents and Radicals
Exponents and Logs
Rationals
100
Factor: 5x^2 -41x-36
(5x+4)(x-9)
100
Find the roots from the graph:
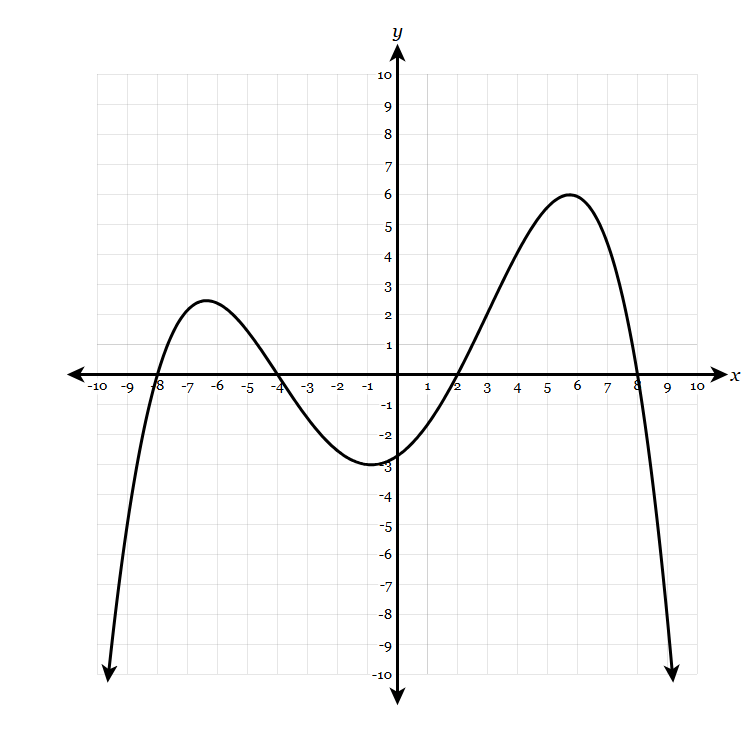
x=-8, -4, 2, 8
100
Simplify the radical:
∛(128u^6v)
4u∛(2v)
100
Evaluate the expression.
log_7(343)
3
100
Simplify the expression and state any domain restrictions:
(x^2+3x-70)/(x^2-9x+14)
(x+10)/(x-2), x≠7,2
200
Solve: 2x^2 -1=41
x=+-sqrt(21)
200
Factor: 3x^3+81
3(x+3)(x^2 -3x+9)
200
Simplify the radical:
∜(486x^2y^7)
3y∜(6x^2y^3)
200
Condense the expression to a single logarithm.
10log_5(x)+2log_5(y)
log_5(x^10y^2)
200
Simplify the expression.
(x+5)/(x+6)*(x^2+9x+18)/(x+3)
x+5
300
Identify how many solutions there are by using the discriminant:
2x^2+4x-5=-7
Discriminant = 0;
There is one real solution
300
Divide the polynomials using synthetic division:
(x^3-14x^2+49x-10)÷(x-8)
x^2-6x+1+(-2)/(x+8)
300
Simplify. Your answer should contain only positive exponents.
(3x^2y^-2z^3)^-3
(y^6)/(27x^6z^9)
300
Expand each logarithm.
log_4(xy^3)^4
4log_4(x)+12log_4(y)
300
Simplify the expression.
(x^2+9x+14)/(5x^2-25x)÷ (x^2+17x+70)/(x^2+5x-50)
(x+2)/(5x)
400
Solve by taking the square root:
2x^2-7=-33
x=+-isqrt13
400
Solve by factoring: x^4-4x^2-45
x= +-3, +-isqrt(5)
400
Simplify. Your answer should contain only positive exponents.
(2x^2y^5z^-2)^3/(2x^4z^5)
(4x^2y^15)/z^11
400
Solve the equation:
-4+log_6(8x)=0
x=162
400
Simplify the expression.
(2n)/(3n+2)-(5)/(n+6)
(2n^2 -3n-10)/((n+6)(3n+2)
500
Solve using the quadratic formula:
6x^2-8x=-11
x=(4+-5isqrt2)/6
500
Solve by factoring: x^3-8=0
x=2, -1+-isqrt3
500
Simplify. Your answer should contain only positive exponents.
(nm^2 p^4)/(2m^-1n^0p^2)^4
(m^6n)/(16p^4)
500
Solve the equation:
log_4(x+6)-log_4(9)=2
x=138
500
Solve the following rational equation. Check for extraneous solutions.
1/(x+5)=(6)/(x+7)-(x+4)/(x^2+12x+35)
x=-19/4