Unit 1
Unit 2
Unit 3
Unit 4
Unit 6
100
Find the inverse: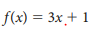 
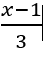
100
What can the sign of the coefficient of an "a" term tell you about the behavior of the parabola? ax^2 +bx + c
The a term tells you whether the parabola is facing upward or downward.
100
(4 +i)-(6-2i)
-2+3i
100
To solve a 3x3 system algebraically you must first use __________ to make a ___x___ system
ELIMINATE , 2x2
100
What two parts of a polynomial can be used to determine the end behavior of the graph?
The sign of the leading coefficient and the degree
200
The absolute value function reflected over x axis, vertical stretch by 2, left 3, and up 4
What is g(x) = -2lx + 3l + 4
200
Solve by finding square roots
(x+4)2 -10= 215
x = 11 and x=-19
200
Simplify the following: √(-72)
6i√2
200
Graph A
200
Factor: x4+14x2+45
(x2+5)(x2+9)
300
f(a) = -2a + 3
g(a) = -3a + 4
f(g(4)) = ?
19
300
Factor 3x2+7x+4
(3x+4)(x+1)
300
(2 +5i)2
-21+20i
300
The solution to the system:
8a + 5b = 9
2a - 5b = -4
(0.5, 1)
300
FACTOR completely:
3n3 + n2 - 27n - 9
(n - 3)(n+3)(3n + 1)
400
Solve this absolute value inequality: 2|x+9|+3>7
Graph your answer on a number line.
x>-7, x<-11
400
Solve: x²+9x <-20
-5<x<-4
400
(6 +2i)/(4+8i)
1/2 - 1/2 i
400
Solve the system of equations:
y = x2 + x + 5
y = x + 9
(2, 11) & (-2, 7)
400
Use synthetic or long division to check if (x+4) a factor of 8x5+32x4+5x+20
Yes, it is a factor! Because the remainder is 0.
500
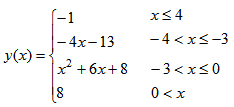
Given the piecewise function above, find f(-1)
3
500
The students in this class built a model rocket. The rocket is launched in a large field with an initial upward velocity of 128 feet per second. The function h(t)= -16t2+128t models the height of the rocket above the ground (in feet) t seconds after it is launched.
What the maximum height the rocket reaches?
256 ft
500
Solve: x2 + 12x + 64 = -10
-6 + i√(38), -6 - i√(38)
500
Solve:
2b+c+z=11
3b+4c+z=19
3b+6c+5z=43
b=2
c=2
z=5
500
For the following polynomial:
- state each zero/root/x-int and its multiplicity
- identify if each zero is a bounce or cross point
P(x) = 4x(x-1)3(x-2)2(x+1)
x = 0 (mult 1), cross through point
x = 1 (mult 3), cross through point
x = 2 (mult 2), bounce point
x = -1 (mult 1), cross through point