Find the slope from this equation.
y = 1/5x + 8
1/5
Find the equation for this line.
<img class="fr-fic fr-dib" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAecAAAG1CAYAAADDSzyoAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAP+lSURBVHhe7J0HoCVFlffPzfeFSTCBDBJMGECMgCw5Ss5BgoAkcTFnvtU1r666K2tCRWBgYAJpYCQLLiCKIOIKKoLkMPHFm7u/86v7zpvm+Zj3Zu7t+8LUf6Zed1dX16lz6lSdOtXVdROhQjw8PMYlaJ6JRELK5bJkMhl3DiqVirsGpCFYXDKZlFKpJLlczt338PCYeEgOHD08PMYharWaFAoFyWazEgSBM7pcY4ABBtmMM8a4Wq0OXnt4eExceOPs4TGOgXFua2uTvr4+d40BxlCnUilnmDHYGGo8a9ISj3edz+edofbw8JiY8NPaHh7jGOYFE8xb7unpkalTpzrjnE6nXRwG2ZpysVh0Rpw4mwb38PCYWPCes4fHOAbG9cc//rEzxhjnO+64w50zvY1h5to86a9+9auDnjZeM960h4fHxIQ3zh4e4xgY27e//e2D3vALL7zgPGcMMob7P//zP138a1/7Wvnc5z7nvGkMN/fNq/bw8Jh48MbZw2Mcg3fKGOeOjg7nOT/zzDPuHMN80003yW233eYWiH3pS19y6XnXjFHGQPOsh4fHxIQ3zh4e4xh8GoWh3Xnnnd1U9WOPPeYMM1PWP/nJT9x09oEHHihHHnmk85q5Z4vC7FMrDw+PiQdvnD08xjEwyExb77DDDs7g/u1vf3PHG2+8UZYsWeKmu3nXDDDKtijMFo95eHhMTPgW7OExjsEUNdPT2267rTO+999/v4v/2te+5q4/9rGPyWte8xpnjAlR4+w/pfLwmLjwxtnDYxyDBWFMV/PeGWB0f/3rX8vDDz8s7e3tct5550lnZ+fg+2WOBO85e3hMbPgW7OExjsEUNtPa22+/vfOK8aTPOOMM9z7505/+tGy11VbOQ8aIW3rznv1qbQ+PiQu/CYmHxzgGhtemtvfdd1/5zW9+4xaDzZ49W5599lmXBs86uviLtBhpgoeHx8SE95w9PMY5bJqaqW0MM98wszEJW3oytjbDbN4zaTn3424Pj4kL7zl7eIxjWPPs7u6WN7zhDbJ06VLZa6+95Nprr3XfNHMfDxkDzjmGmWvzuD08PCYmvOfs4TGOgcHt6uqS4447zh3nzJkj3/ve95xh5vtnM954yqzeBhhqDw+PiQ3vOXt4jCHM4zXDalPT9s0y+2TjCdt75blz58oRRxzhPWMPj0kO7zl7eIwhbBoa40vAKBPwkh955BHZcccd3SdTp556qtxzzz1y6KGHuuf89pweHpMb3nP28Bhj0ATtvTEeMecYba7NO+aceBaEmUft4eExeeE9Zw+PMYZ5wBhkm87GEDONzfacnFsc75rZuhMvm3seHh6TE944e3iMITDM9r6Zc4wwn0pxZGrbfpvZvnXmnL20+cYZQ+3h4TE54Y2zh8cYwrxiAwbYVl5PmzbNXZvRxrPGW37ooYfk7rvvHnjCw8NjMsIbZw+PMQTGmcVdBIyvec28WyYQRzAjfuuttzpv+r777nPPeHh4TE544+zhMYbAS2bvbALnGFwMMUbaprKBedd33nmnFAoFmT9//uB0uIeHx+SDX63t4TGOQfPEWAPeN2+99dbyzDPPuOs//vGP8uY3v3lw2tsCC8mG7rft4eExseA9Zw+PcQz7dIrw9NNPu0VieNQY3ttuu+0V9/GkiceIc+2nvT08Ji68cfbwGMdguhtDixF+4IEH3B7btovYXXfd5aa/eSeNwcZbxjAD4nnWw8NjYsIbZw+PcQwMrr2Xvv7665133NHR4Yzwdddd56a0SQO4R1pb1c27aQ8Pj4kJ/87Zw2OcA0Nsn1b19PS4d9BcE88nVfyUJM0YA048YErbe84eHhMX3nP28BjnYMr6D3/4g/T39zvji2eMYSae3cL4tIr9tzHQBHvXbNPfHh4eEw/eOHt4jGNghJm2fvLJJ2XXXXeVXXbZRaZPny5ve9vb5J3vfKe719fX5wwxxhrY+2Y/KebhMXHhp7U9JhD45pfxpB2HYuivNK1p7Glpx//41LxkQHPdZ5995GMf+5gccMABg/cwznjVeM22QCxqsD08PCYWJrznTGdlC2I4t7EGq1uHfv8ZRxgJwz3jQzTU1hgqFX4akRXIWpdSj6sb1nrd1vTUhTDQUNUUldVBryvVQKr6yOoQSjWoSDUsulCnM1y5mhPA0E+aMKjoJ3j44Ydljz32cN4u75L5jvl//ud/3D0WdaHDUcNMXhhd+1Uq+wba3jVjmO07Z54bWh4ffJhIAaDvtBfazdB7kxkT3jjTOVkHBeycjomOyu7HFeg8hw4CohjuGR+GhvpGG8MFDA31aMYYA11H3UCntLq5nUwM1LX+I3WSfxqXTvNLTxgvCwlJJTUkUi4MpdfsQJltYRbvjFlBTTzG+Nprr5UddtjB8cjUNGl33313Of/8852Bth+2wEj39vY6PSOOa2TCNUaZa4BBrsuqbqzpzIaWxwcfJlIwXaa90KcTN1w/OxkxKaa1bUrPAEt0VFRkND4OmAIZhl7TgXqsCWuWD/K0wQ/nUfnW7w1ckE9iSF5h3Uwn1AivBmlIi5HXvAbSxAUMJDpIWfF6Ma6cs+r6oIMOkueff17++te/uji8Awz5tttu66auv/e97znDzT0MMB0Uxv2QQw6RL3zhC/Le977XXXd2drr75I2cTOeg6/XPYyID3ad/R68ZeJrDtT5gwhtnKg5EKw2WrDI9xjtGNh6mosM3yvrz+NT1k3qdR3UBvHqDjl9HhuojBpNPoJjO/spXviKf/exnX2HEOceQ8z0z+s0509jc49n99ttPPvnJTzoDjkHHaJvxhga0SDt00OrhMRFhbRhE23W0TU1GTHjO6HyiHRAVRgf26p1xc2FK8mrBYySggq8ewpB6NO+XqVy8UX7XeOB1QsCouqIWT2UdaNqBELp7Va0gHbyFVTXdZQ0c7R0zeUMjflBOG0RiaDG+fBqFV/y6173OGVg6GdKQluk7Po0iLbpt3jbgPsF0HoO8atWqwelugq3B8INTj4kOZoZoF+g/gbaL/oPJrt8TnjtbKEAAVonAOqk4YfReLXg0DpMjjZLGSaO0NQUOazCyPJpI2iBJB238e8U0d7wwvbSyYlQxqM8++6y7R8dz5plnDsbPmTNH/v3f/93xDL+kQY8xulzDN+fkh/HmXTSbk5AGg46RxuhbB+bhMZHBjBE6b+3A2r+1j8mMCW+cbSoPI23G2AyjdepxAqWxQEdr3o8Fj8YQnX3Ai04m65twgHJZ5ZtIY/nUIyYoeO+sob7IbOCag/u32ihzrwXq4ToWDC8BXqxTsffDGGYWgXHOojAWg1144YVy9tlnD3ZMgPQAPSMvDDTvp3nfTJ4YZHSPNsDRaHl4TGSYLtMO0HFr+8RxbzJjwr9zpqNbtmyZ26TBVrwSqEg6srHqoEysvoMcCTY+HH4ggxzrhq3+DhV5Egr9JfcjELM3mqOp6gYZJMIB4zwg/9X1AJ0BA+5orplus0BZ0VE6FwaQXDOgXLx4sfzHf/yHe3e89957u/tWVhaC3XTTTTJv3jznDf/617+Wr33ta+4e6aIDPzorznmHDYwG+m+DVQ+PiQp0e7PNNpMtt9zSDVZpI/Tr6D39wqSGMjvhsWLFivD3v/99qBXpArBjK3DHHXcMnK2mq4bEHeMGfC9fvtydx83/0LyfeOIJF0CcdEG5XHXHmh6qlTBctbIvPOaYk8NH//Jc2F/WOL1XqgVhqdKv5/1hsdQVVmt9YRCWtUx6V++FVAnFc0XkYnR1ZHUZ5S1a52tCqVQaOAtDNZZhoVAI1esNv/3tb4dqRMP58+crb2V3z/DpT38aKx0uWbJkIGZ1GTgeffTR4Z133umu44bxbPT//ve/D9Z5q2BloJ0/8MAD7jwuPRsORuvWW291R9BK+gC+V65c6c5bTZv6Vudn4Kq1iNZ5FK2WwVjA3AcPj3EJ1VEXbDpLnUJmsZ13uNFGm8iH/vWTUiiL9GkoVGpSU8+yv1KSdDYn/cWSZmBe8sAMRt05VeB5WogPeMl4s7wfxpNlepoRv3kBf/nLX5yXCz9MVQPeIxNHGGtQxvGI8VouD49mwRtnj3GI1YYTo1U3zhzplHkPVX/3uunmW8nSVf1y7kf+TQpVVeZcWm1vRpKZvKzo65G29k4JE0xl67OamwWz0wNXsYJyMhVtBpnVp1zzrnmbbbZxG5HwOob7Zox///vfO6O+1157uWsPD4/1D944e4wz/LMni3HGYzZniesgCGTLrbaWMJ2XRx57Qj726S+7vcMKmqZYTciUjg2krOlq4YBRN4Ps8jGjPGilYwOGGK+fI54xgw28aOLYH/uBBx6QD3/4w86r5h5G+7777pMvf/nLg++Vxxu81+rhET+8cfYYp6h7zuHgXtpMZavCqsZmMvUFT5tsvoVUwqTU0jm598FH5Itfu1gKFU2n1/1V9bYTWanpM7UBLR800A5EWogPtigLD7qmLj/T2hhqprrPOeccufjii90OYTbd/ac//UkuuugiueCCC8atcfbw8Igf8fZMHh5rheGNER5lHas9Nry3fFubbP3a10tZ0hKkcnLznXfLT3+xoJ6LGjrMOk8E+q9GbIKreh6s/q5vcBIvGERQVgwyBphtO/GgiWeK+/TTT5e77rrLxZMOrxmjjfHmmfGI1fXh4eERF7xx9hgniBrm1ed8r2yfC2G8cCZ554wXilf6uje+QQLeKyfzUgkyMnfuQrn+xvvcD2L0lfQZlwuGmc1ACJY3BqY1RoYfvDCwJSeBqW1bFIax4xxYWrxo7zl7eKy/8MbZY1wjNPOqhgojxufKTG1jvMCWW23uzlPpjBrntFTUSH/ju/8jCxbfK6ls0nnPgap5/cjSMDXJ5kDXs44VeMAYY4wuPDDQ4PtsjLG9Z44e8agZeMATU+EeHh7rJ7xx9hgniKoi5/XArl42LQz01BnoIKi5bTnfsN1r3R7a6XRWveecFCQnvbWs/PcPLpW//aNLeONbCBNSDAdMc00zqPELUGquW6D9rLoGbCZiq7GnTp3qjLFdWxquCcarxY8lKOd4xHgtl4dHs9CC7snDY7RYO3VMqD/8ljdPl1RYUW+0VySdV2OcllR+qvRVEnL+BZ+Rvzyxip5cqqKetVr2UL3SoKgmPJ+S7r76d8Uerw4GRuMR47VcHh7NgjfOHhMYVcmrBm+88TRJZ/MSJrLqTeelUKyol5yS559fIZ/97Nekq0ftdiIlKb0vmYQkcvWNTTo66vtVe3h4eIw3eOPsMWGRdG+TRXZ482slmUpLd29RkumcVIOkFEs12XDWJvLii91y7tmfcwvJuvsKUq5WJJHNqCEPpL+/r56Rx1rBe60eHvHDG2ePCQv2/eKt7Tve9mY9U0OdVu9YY3PZNpFUXpav6pcwlZHnX3hZPnbBhTK1o02y2Q410FX3OVNHe32FtIeHh8d4gzfOHhMW/EwzC8Pe+oY3SKJWlLZsQuPKUi31SUINdZYV0bWq7LXXHvKFz3xaKuzxqUin82rIs1Kp1lqxYHvSwS/G8vCIH944e0xMDPxEZD6Zks02mi5T2xNqfF+WVK1PprRlpL+/V4KUyPsOP1A+87kTZNON26WzLS2lQk2CWkINdMYt3Pbw8PAYj/DG2WPCgu+VaxWRnBrh7V+3pXRkypKudcu2W8yW9nxGyrWy3Hr7LdJdIJ0mrvKrUCmn9KVyTXIDnzJ5eHh4jDd44+wxofCKGVX1njNqmNMat/3Wc+TQvd8jN1z1M/nRdz8j6iRLh3rQvYV+WbhwiRpiTYQ1VwMdqEVP6UN+i4+R4b9z9vAYG3jj7DGhUSj2u3fPHz73NPn3z5wnW83OyIx2kbPPOFH6ula6lcWXXX6lptPELNkOS5LO1LcEZeW2x5rhv3P28BgbeOPsMTERorqBtLdn1BnukfZkza3cLvX06x+RQ/Z9t8ye0SGpIC3F/oT8Yu61EqbyIlmRYrlLitVeCd2mnh4eHh7jD944e0xoVKolacumRWplkXJBZkxpl5y60nOmihx3xIGSDCqSSOVk/vW3yfMry25XsHwu5/a8bkv7TUjWBd5r9fCIH944e0xopPjFKr5x1iM/FlEqVaRSLklO773/iANk1rT6Lz+90F2Wy6+9VXIdM6UsKenMd2q895w9PDzGJ7xx9pjASKpRzkulWP/ZxWRKrzNpmdqRl7DcJ7OnpOTYI/aTdEY9bE13+aJbpKsqUqhk9Lms1CoBP4XhsZbwi7E8POKHN84eExdhSoJKUrLpTlXklFTCqgaRqoZkrSDZREFOOOZA6exISDWbledWFeXHlyyWTCbrFpG1+0+pPDw8xim8cfaYmBjYhKTG91BOi5PuS6l0ip+DLEumja05azKjLSFHHbavFAvdkmvvkPmLb5fnu0TKFZGAXUj0P+DAJHf9krwtEJd08aF3GD08PFqECW+c+QF73inyvpEjU27E2b24wQ/jQxda9qP5xPEOtNULZ4bSawb94fIYblpzuLh1o49Krg6hs4ir1TQMrU45ar3zclmRCGuSS9Q3GMnmsno3r3ezkqqV5YTD9pNNZ/AbyUV5sa8oVy/5X0ll68+I5lerqMetdwtBKH0lfgyjJkGhR6RS1nOFZtqvhpxJ8HK1pGWo6bNJCUbxoTQ6AdAP9IKjnQM7AktrcaZT1WrV6RNHYL8DzbXJmHT2PODZZsDoGh2O1tasPHHD5GFtC6ybbq0brE9B7tDnnLhWlMFkDD3qAtoMPlvFP/Si9W/823ncgC6/b87RygD96PVkxepeb4IChQVUmCkORyrOlDnOYB0VtKwsXFtZ4g7QMsMIfes0oE+jGu6ZtQlRkC8gnnNLY+fA0hgszboGeLD6tA4KOD4xokpOk2lPoX80hBrBNb9MVQsSUir2yybTp8ihB+4tKSm5PbUv/sUV0tWvz5BXoB1MMnTT4alkQtpyHfX83SBgoAwDPNEVmYyJT6bqtKPlHRrMkAJ0hTjy4Ic3yKe9vd0d6YDsvKOjQz74wQ86nnmeOGTA86BQKLh8eAb5lEoll85kT+cNDauXRgN5GW3ypuzEQ39o2mYH+DZEywGaod8jBdM9aAPoUx+gFfRNxsidwRflyOVyrgxD08YRoGe8G4ZLF2ewvgz+ubb6sHqYrHil1CcgqDQCoIMyZaICqVS7jitAh4YDuAY0KBoxYWj6ZgdTXuOXa5SWMkTlsa4BkDfBGgPxnFsaOwecW3pgadY1wAO8kO9wvNJXp3CKU2oENWBgU1qU+jElmXTOTUmfcMwRMiWXkWxCOxw1vJfMnS8Vzb+qaZPUk6bBkeZYqyqvuOQsMEsqDX0ml1IeNaeEeud48xjEWpXOa808YsjQT87RE3gxL7etrU0+8pGPOF6s8+HY29srP/7xj911X1+f0yOTv+WLIcdIWx1zP5vNOhockQ2w9OsaoAmsPvP5vAvcI25o+mYHeEdmAN6s/i1+uGeaGaBjOm2DEpNFM9rXSAFwNFrRNhDVh7iC0SOAqNxbwT+0oENAry2eclm/P1lRr/0JDCrPGq91SAAlIhAXZ7AGAjhHYYinIxmaNo5gnYfRp9FaZz9c+rUNBuuQQPTc8Gr3h8tzbQO8RDskwDGlBpP3xjXeHet9fqEq5FrT1fSckM3ltVOtyIZTRU486hAJ+ruwvjJvwXXSVWS/EjWamp4tQBPa/1QZZ4WqTypXjdE8ylKtFNQsqzyVhnYNjjZ1nkqPPDODIcPIAuqKczqav/71r4PeM3lZGtMl+EWv8aI5Jx7++/v7nWHu6upyxp175MfRDDN5mS4MV6a1CSZv8rdry7sZ+Y8U4IUjgC78AWjbvTiDtWNAHVj9QL9VbRxaVv/Ug8kdeQxN2+wAXfQwWue0R2TfrD5mTQEZQwu+oQcoC+WiPU1mTHjjbApDhRmsUgnWoOIKwAYHIKo4Q9PGEeDV+OcaumawiR+afm0D+VjeHIHJ3BC9jqa180YC+ZKP8UUc18TDOwYaLxmvOYnnrNdpvZ9RrzmVzEi5WjdeWU1y+gkHyhazpktYLUl/JSGXzr9RQk1X1DTUZJs632pv60ZXnw3IVu+nNX8mp7WLqn96paymSahlGFreoQEDjEGhY6H8dDKAe2DatGmD9wC8oU90SBzxjrnHNffgBW8aw2wysOegQ3qeg87QsqxLAByt7LQpN2vQpPxHCvDC0XjlnKPJIpo2jmA0gOmd6WQr6BPglwBdaCIT6oPr4dI3M0RpmAygTbC6iTMYv5wjA/SOo5VlMqMu8QkMKoqKs4YDqFA6KhtlxwmUBe/IGpCBMrUCNsVIOWwkaw2KBtQoyNcaRDQgbxoNgfOh9+25RgEP8AJP5AuP5EscvLs5a6Dt1E5fIflkVvNQndCbnWphD9xrF8kntYxqyH982dWygj2302o8y5pAq48iKxkp1ZQHprD1NhudAFaDc480GMcgHHlajTLCA8aVwHVPT4/84x//cDzw/tD4gT8MH0fSYWihY8AwotscyZN0yB+YbHjO5M51o6DMyN7KSHkIVudxw9o0tKAJ/62gGwW8Uw74tvNWAV5N16nzaN22ohzQgS7B6FEPrYK9SoAm/TnlMN1rhn6PZyRU4K3TtJiwbNky+cMf/iCzZ892lQlLdFpUIJUZJ2iwjzzyiGy//fau4UCT0CpFhveZM2c6xaXThi40OcI7ZWkU5EcHYSBPjMrzzz/vrjfZZBNnVIamaYZqkSdyNZ44Gq/wPmvmBi6dmil3dBj4zEq7NUkk66Punu5umTptA1nVV5GPXfg1WRW0STqTk/1320mOPmgPaSv1Sk6NdrlWdRuZ1BL6bEY7gUKPaHegnrPmn8hImND81Gt+7LGH5c1v3l76+rHurz4QMzmgJ1Y/1Mu9994r559/vpxxxhny7LPPys033+z4fNe73iWHH3647L333k6H0ec77rhDLrzwQtcZwT+yJx5DZTr34IMPunh7Dw0N6qQZQH7QxkCsWLHCXU+dOrUlnSMygy48wfPKlStdO4dv7hEfJ0zmnZ2d8uijj7p2ThyyZeASN31ow//f//53x7cNxuDfdCpOQGPp0qWOHv0MukYwuUTbfBxAj6nzXXbZxZ1Dz/oVymTymIyY8MaZCsITeeKJJ2SrrbZycVaJKG7cykMDpeFst9127hra1gEDFDlOQHvOnDmu84jSRS6ABtQoyINA/uRLw8QQvPjii+7+Rhtt5DorGgr0LW0zVMvyiPJF/iyaevmlF2S7rV8jgRpSjDNHNSPOww2VbYxziIHW9Dm9qlTU60nn5YdzF8nF194tpWpCZnam5YoffVfm5EuST2iHG1Qklc1JJaWhVJY253Wrka4iz6TzqEM1/n9//M+uzplKX5Nxprx0cGY00Qfirr/+emeYDzjgAPnSl74kr3nNa1w5v/CFL8hFF10kF198sTPS6C/xyNxw3nnnyamnnio777yzu0YHGbCQhvx5Bhr2bKNA9rQl8nr55ZfdcdasWS6+GXU8Eox/pvNXrVolG2+8sZMl/MXdvuDRdPuxxx6Trbfe2p2bbOPm3wYAtHMGwegStKkP6jxu/qHP+gb4xDgDkzvHuPmH9vLly2WnnXYa5JWj9QfN0O/xiknhOTOyevLJJ2XHHXd019ZoWlVxd955p+yxxx7u3Oia8sYNPCYGJRtssMFgQ4mLf8vTjsgcYFiG3msmonkDzvHgnvrHE7LjDm/VCIxzqv6OmPt6hcEkdVlPWb2dZreSUL1MyarXnJCdDz9P+qppyVSqcu4pR8qHT9lT71T0flGfSUglzCudtDCpnNRHlYT2CpojK8f0/M47bq7XuaZZk3GO6oEZODpbDA0eEdfWyXFOmne/+91u2hv58k4aWD4cjzvuODn33HNl9913d/fihJXL6DMI5po6bxWsDLRz6NNRW1wrYLRuu+02N6MRjWsVfv/738s222wj06dPbzlt9BB65vy0EtE6j6LVMhgLvHqv4uExgYBhHg4YZnUitTXrH7zJhAa1saeecoIUi/1qb1Ny6eVXSX9ZpBTU1DDX3DvmbCotNbXsLtv6mEBbCyeE+juw0cAMM54sHhcBb4RV2HiDnGP4MMoc8Ybe9773uU6J6eyxBp3geMR4LZeHR7PgjbPHpIf79SlWdDuvN3Qrso88eBfZZOZ0518XyhW55IqFEiZz6iHnpb9SlpKGtBpWtwgMO2zBGeiBqUTnTo8MPn/CmGOozUjz/vSSSy5xrwe4x9GmrknDtB1ekoeHx/oJb5w9Jix4nzzUQIaDbm4dbByWTqcGjCt/QuHnn2e0iRz+vn31suTmwudff6M8v6pPutSFbstMVa+5InkW++sj7jElw7vmQcNc96lHBAaX75IxuAYM86c+9Sk5++yznYHmnr035vymm25yU97vfe97B54YX/Beq4dH/PDG2WPCA1PhHNpB1N83g4Se8R4aoxe4986hxqmBVVt57BH7yIwZGb2qytJV/TJv4RLJt0/Vq6S059s0T81FbXCYrNUXmL3CHtN0LLw68JJtQRFGjSOLej7xiU84z/grX/mKWwVMPDjmmGPk4Ycflk9/+tODcR4eHusfvHH2mARQNU6oHz1gkTGCg/+Y0nbviJOSYGV1MinlSlFyamg3nSZy5OH7SCpdk1oqL1cuukX61JFWx1YNetLtDCaJshrlstryih7Na1aESpMwAniXzJQ1YPoarxnwKdJDDz0kb3/72+Utb3mLm8bmPqtTr7jiCvn85z/ftE+hmo3Rvm/38PBYd3jj7DGh4aa2DbwgVuDlGrhbqVbc/tmJgcVZbC2Skfo+zccfc7B0dGYlmcnJ8lUl+fkvbpV8vv5cJoPPXTfOoZpncsfg1+9qGBgMrAlMVfPOGSPNoMEWiPHpG6tfL7/8chfPp1Ycb7nlFjniiCPcedzf0Hp4eIxf1HsKD48JipG8uHSqvggLI86e2+VqVXLZnKTCQNpSCZmeT8lRhx7kPNq2julyzY03y4sr1CRX1UvWtAl9JuWMMFPlmGiOfLqlV6NwIDHKTGPjPVMOe69sn0XhMWO8uY9BBvb9qhlyDw+P9Q++9XuMM9iiq6HBYBYR1a2rLwY6qfHDBf625drdMZVISzadc+eZVFa956TwA5EnHnGwzJkxXcJkKC92d8kvFt4gkmM7E80/SEuqXN8hLClZKfD5kz5TqlWlymqzEYChtQGEvUO2DRTM+LJgDDg+zLsfSDPWGK9T2OO1XB4ezUK9J/DwmGgYxfvefwbPrA7O/FVLstGUnBx5yEFqiCuSyWfUe75JlvYGUk3kNQF7h2elUuJXqVjQpR4wzyXZW3zyNx/z5scbxmu5PDyahcnfu3h4rAHpdP3HUU44dl/JJtQ4p0LpXtktC9V7DtQ7CxgEZNVAs5uJAoMeqsOcUseNSW4PDw+POOCNs8d6j0CN7TR1kk95/5FSKxdxy+SqBYulq5/fe2Zb0JSk3JQ0e3erQVfDjNMcBGwaMvLU9mSD91o9POKHN84e6zXcu2m1NXjDJxx9oExrS8uUKVPkpeVdMm/REqmpTe4PEoIZxijxK5EZNc4Y5lFuEObh4eGx1vDdi8d6D2as2zW0aTjm8IOlWipKW+dUuWTeQnmpRxNofFUNeCqVcNPZouc1Ps9aT5uPX4zl4RE/1s/exWPiI7ohSAOolivOE65Vy9KuXvIpJxwiKeHXq5LS1V+URTfc6lZn89kUNinpXjrX98B2VtrDw8MjBnjj7LFeI51JShCWJZ9OuV3DOrIip51ykvCLVfn2Trnk8vmyol+NuKblJ535/pj3zNks3yWTg29CHh4ezYfvWTzWYwRSUy84qS5xMlRfWe0uDeLE4/Z3u4ZVg5oUyzVZdO1dbtkXC7fLVbbUDCUM2LV78u997b9z9vAYG3jj7LFeg99urvKDGAEGN3C7gdEoTjv1BCkV+ySRzMpPfnqJrOLdM9PaGTXIyYS0dXTqYfI3H/+ds4fH2MAbZ4+JiXXahOSfob6zdvQ1bQlpSamx5f0z4bCD95bZM6dLpVxULy0lC69Z4r5qDsKE1NSQ9/SVpL+/XM/Ew8PDo8nwxtljvYba2cGNSBKJ0P12Rk6d4w3c7z0f6Ay1BFWZv2CRrFTvua+kXnYyJ909vZJvz66XS8K81+rhET+8cfZYvxGy/JofxyhLVUPo1mnz+88iRx/+PpnWmZNqtSTLly+X+Yuulba2vFu9ne9od++hPTw8POKAN84e6y3qv1SFa1xvBvzmBN8x18o1SatzuPF0kUMO3l/a2zKSyefkinkLpKsgUtF7mWxe+vrqv828vsEvxvLwiB/eOHus50hKsVKVZDpZ/4aZGDU+TGdXyiJnnHqY5PNJ9166v1BSA32DGieRYrki7R38MIaHh4dH8+GNs8fERJM2Icmm6r+rzIdRtaAm5WpF8pmkW7Xdlhbp0HDskQdLpVaVRK5d5l27RFb1sVtY6hXvXlksRqjH1L+Frod6nIVovIeHh8erYcIbZ7ffsQbrLJlyc51tC6feqtXqwOYU9Sm/SqXifpeXH9WPG0YXxMFzlAfL32QObYJdg2gZ1o1/VHK4UMfq7KFtO3WtG8iKBWAdubwazoQktM6S6awzsln1ovOaoC1Rk1OPP1zS+Zz0BSlZWkjIz666TbKZvBpwNdhBKKVy/TeeCT3Ffv2rdVIr1UP9SvrUuJe0vG51OOXWyFKhqjKqyxF885vfdPI76aST3HWhUJBSqZ4HQK8MQ/UrWicgqhfNgP3ONKCM6HwrAB3TKc6Nb47N5vHVYHSgaXKmTNRPq2Dti2Mr+pUo4B/dMzlYGaxMcSJa91EZEN8K+mOJ1S1uggIloaIIKA8VZh2JVWicAZpGn8ZKXCaTccpsA4Y4g/GNHKIKDEwejQSTJefWOImDLvwROLd0RhNEO7N1DUYTcA2P8Eo8dIemX9tQz7h+iDYHZ7jVkGbVOHeqJ336aadJmEhJoRLI1Yuuk66+gqSSGamxeYnyWR7oL9vy7RLwKxrOADNoU6OsZUZOyWTaldtYyrEsXI07z//2t7+Vz33ucy6+WCxKX1+ftLW1aZqcM9BWzyZT5ECeoKenx90nzuRl9TGU37UNJmOTOfla3lwPTd/sYG0IWpQlStdkEWeAFmWAf0CctTXqZ2j6ZgejG5X7cOniCtCHLn2a0QbW7oemjyNAK53md9Xr9U+ZiJ/sWN0bTVBQaaa0gEqjQQFToDgDtDHEnEPPaJvyDE0fR6AM0CZEGzAYLv3ahlcDvBq/w2G4vNY2AONlKJ/DpV/bULfCTGurHN1f/hFXLz+dcKFUliMP21emtuckGZR1ENYnd93zGyko60FSy8L7an2Ez7I4VnFw1RCzWUkyiU+uhtSNAALNTw98o619brVKx1Ovr3POOUde//rXy+zZs51M6fg5Qp+OERlwLJfLTt9MJqTJ5+vvvrmPbIDVzVB+1zWYvA1cN6sO1hSMB6Nn9R+9F2eIGkczVARAHQz3TDOD0QJGj3oemi6uYLKO8so5sgcWF1cARo9jtByTHatrfoKCSsOzoMOyhkOcNdxWANo03Gw265SHcxqQKXCciI4io8oMog17XRHN2/KDL+hGg/FKmqHlaARGczgeodtcvFJfoJhJ5yWv9To1J3Lq8UdKNqW8VsvywEN/kt6y1r0+Qin4feeEGt6axrFpiaQy7pestJR6j3Xh2sFUVUdSufpvQ2sSvqtWTZWPf/zj8uCDD8r3v/99Z3w7Ojocf/CKXJGB6Tc6RsB4E0dA1/CeaQek51mCya4RROXOOYOFqIceN6J0jLbpQCvKYDKEJnVjwCmIvnKIC6YDBOra6gNEz+MEdOHd6HGk7bWC/nCDTYtrFf9jhcZb7xiDyrIOyxotlUejakXjhcYGG2wwSMsUh7JYeeKE8Y2iUgaOzaQ9XAMgDj6ZciVw/mrpmgHjh/yiPMJ746DeCMir7gGDemxSShW1uFX1TvX24QfuIRtv0ClpreKu/qrMXbDEvWcuK5t8gpXTeO6lMyl9VjvVBJ9qBZJRXUzrdSbB1BxyYVClz6hFv+eee+Tb3/62/L//9//kHe94x6DhswEPPHJEztxjytvuYyCIp+PkN6itLpANR9I1CmRtcqdNMRAwz60Z+Y8EaAFoDeUL/uMG9MwoTp061RlkGxQ2Y/AzEqALHeoWfuGdOHShFYAWdQB95A+QCWWx6ziBvCkD9KALuI4eJysSyuCE5pCGg9fw2GOPyUYbbeSUlg4NhaYjs8YdF1DQp59+Wrbcckvp7+93Xg8NiAbcisb77LPPyoYbbuimNq3Dhi5yoGpNodcV5GGN0FSFI/Sef/55d73JJps4WVu6aPpGGzA8kYd1TPAFT9BjY5DNNttsIOW6QDt89WpBsqbGRo1xoFVG1x8OFBtvWLsjyXZOk55iVS5deIPc8Ms7pFAMpLM9J9//zhdl9jQ1ioWSGueBld9qqUtBUY2v5q1ediaZklqVSfOM1IK68cxl4aFfjjrmSFd/P/rRj1y97bbbbrLvvvvK17/+9cEFRw8//LA8+uijrqOaNm2aXHHFFfLOd75zkHdkcfLJJztZWZ2j93bdCCirGQTa1YsvvujKOXPmTNf2GtWvkQB96FD/1D06t8UWW7hzeGyUv5FA/tDHOD311FNO5pQJ+q0wUNQhbe3xxx937QyerX+hTJzHCfJftWqVq/MZM2a4gSBlsD6GY5xA9kuXLpVddtnFXVMfrZL9WCN+6xEzTFEMVJ4pbNwdB4AGCkQZzICgNJSjFcoDDWhbaDbNqGzJ2wKARwIYeg9En20GyLv5vFJ+Qr2srN7mHXTgsuYdZ0ay6YysfOE5SZT65dAD9pB8Rus3lZV+NbiLb75L0zJ7obIISppVWfgJSrXM+nhW47QTq6g+VtQDSWbUs85KZ2endHd3y9y5lznD+5GPfMR1wOgRBhgvuKury8kWA21GiCMLxUhnOk58e3u7k0fUu6IDowNvFENlHa1v4uOGtSfaGQGaHIlrBn8jAfrQM7kiY6PfCkRljOyhS1midRIn4BUYbQLnyMJ0IU5Aw+jZtZVj0kOZndDQBhrqyCp88MEHQ61AF6cdk4tvBaBzyy23hNqpumv1YgbL0Qo89NBD4bJly1w5jC7HZvJPflGeTL5PPvmkC5wTZxiavlEMxxs8w3tjQEblMAi17mqav16SdzmshFqLGvRuRUPB7oVhv8b9xyXXhVvvfVa4+e4fDHc49EPhM5qwqPeCWklDUZOW3bPdVS23HsNqJawVNCMVUbEQhhU9XXz9jaF2L+EnP/lJUgzKTz3j8KijjnLlMETlq4Y5PPLII8N7773XxZlciCcYos83Asuf/AhPPPFE+I9//OMV9R0novRfeuklV+fRuFbA6N12222OpvHeKhlA549//KPTeaNJXbeCf3j/+9//HqrnPigHjq2SfbSdQ9fKAFol/7FC/EPfmGEjaeXFXXNs9ciWkay9/+QIbVUidx03oAM9G2HDf7NHlpafyRhaBK4Jdg1aRZ/rZshYORg4q4N8VXucH02o6e0M24UF6qVVS8JLkpOOP0Qy6aQEkpau7qrMm3eb8OuRTJEHiaKUav1SqrKCn2lufSDA01FPuop+iPvRjH/91/Nll13eI9/4xjccX9rZacLVvA7Hr50T8LCjeo4OEgxWH80EeVIm5G4eVdwwOUCbmQPkFI1rJYym9TetkgF0mE7maLTNe44byJoAXdM1jq2SPXSGtg3QSvmPFVqr3R4e4xLa2WujD+vtfgD1C7UHrAdTA1vRxhJIudgnbRq3267vdp1GGKTk0suvkj41vOptSzmsaaeRlFw646az+aloVmYD8qdvefzxv8izzz8n99xz32BHx1Q2R97vXXfdda7zvfDCC+sPjiHoBMcjxmu5PDyaBW+cPdZrJF5pkQdBLAEb4AbruMBqMPleOa3X797pzbLZxjOdcS2Ua3Lp3EVqfPNqYPPSXylLqVIUPmHGuPdjuXG51Uj3F4ryjnfsJMuWLZNAM8fI4IniCbOwi8Vhhx56qHvX/MUvflEf8vDwWB/hjbPHeg8WgeGHmS+WCJMysIhbKhVtJGm3nstZ61wur050IBtMy8vhB++tnnPRebwLrrtRXuzql65CWdoz06Ra4qjNi2fa0m6DklpYlbZ2fZ7PqwYWdzFdiYHHMPNKhMVeTNfZa5LxCO+1enjED2+cPTxoBmwIoobUHGkOGGgMs3uzzWdSfPOshimryZPVXjnikN3VSGelGpZl6ap+mbdwieTbpqshT0tHW7s+X5MqP5iRVg9Zn9FoHQDUlBrfaOfcZ3fRd2jVgU9EMNCct+q9noeHx/iDb/0e6zGwmPUmgAGO+oN405hNpqbZGzuNJ6sXNfV0+Z65VuiSjaaKHHHEvpLOqMlN5uSqhbdIX4mNE0TSibTUqiVJpwLpK3arwS5qfvVv7zHI5N3fV/9mFGPMp1QY5hdeeMF9x8w5XvV4hA0oPDw84oM3zh7rPTDKdcOsf9V1du+hMc5caiweNcY7mbJv6vUqKElZjfaxxx4s7VOyksi0ycsry/LzS26RtlzdsKczCalU+6Q9n1bvuiLFSr8zuswK9xUq0taRlVrtn1e3M6VtK1Q9PDzWT3jj7LF+Y8AmrjaNQ6CGNJdKSS2o7xSVyKjlVePckcvKlHRKNmhLylGHHqgec1GynVNk0eJb5YXlIpUyBjyQDNPUrPQOU5LPtGscC8Bq0t6ecQvJksn6phKAqWwMMzve8d4Zr9rDw2P9hDfOHuMM+KjDBYOZUVS3Ceqb4PvNlPu2mf2v1VauzloDK7OT6uqyBWc6zSKt+g2mrdVflml6ddLhh8oGMzuknAnk+Z5VctmCJZLOJyWsMn2tOQcZNfDt5C6BesSplHrU/FQkmUdGBWak+awKjIfp4/E6he2n1j0mO5rQu3l4jAGavH8OXf0ruvuBCxfPFHf9cuAk6eL4fDkshzJ7aloOV+85CIuSbsvJtTfdKMu6Aqm576cykk6mparpEjrGyGbqe6Cz3Wd6Aiz48t85e3iMDbxx9vBoAAm8X8VJRx8obVJxK7lXdnXLvGuWSDmVcd8yp9QIp5L1vcgSaabI8bxpfJVXDgg8PDw8BuCNs4fHOgJjy2IxdhCbmRU5/YSjJSj3SS1MyNxFN8qqfn5Osj5VnU7Xp+bdbmNshchUvVv0VY+fSPBeq4dH/PDG2cOjEahxTqiZTlVFTj3iYJnalnO/OvXC8j6Ze+3t2sLUPw6q6i3Xf62KdWLsww2SzI17eHh4DANvnD08GgDmNZ0MpVMd5M6UyHGHHexWdec6p8slVyySl3tqaoxz6k3zO89qmNWY66l62BV9cmJOavvFWB4e8cMbZ4+JCVZXjTn40fuSpPUYlIuS19Z0ygkH6XVNY9LS1V+Wa264TcrazIIUK7f5VaO6SXYGzv1klYeHh8c/wxtnD48GkFGjy5acmVTaLQbrzIt84JSTpFjsl7aOaXLJ3PmyohBINUxKVVMyk822oAk+y2KzEw8PD49h4I2zh8c6wi3qCqvul6oA66Rw6E86dg+Z1p6VsFaRnmJV5i5YrHa4TVOrMQ7Vy66pOa8GEqYyUqvUvWd+mYqFVhYsbqzhv3P28BgbeOPs4dEA0mok2FgELxhbyrfPhDNPPVaKhW4Jkhm59MqFUtAktYCtO9XLziYklUlLqRxIMl3/IX22BeX7ZwyyGZ7xsCp6vK7MHq/l8vBoFrxx9piYaPImJOuGJBPV6iHraSrFf+FXItX2yuEH7ywbzezQuykpFkUuu+I6NcApyaQzbsq7v1yRGsu21RCzVSfGht905hzYT0l6eHisn/DG2cOjAQTVsP6LVQBbq4d8WmRGuxro9+0rtWpZneqMLFq0RJauLEtPf7/k8nn1mquSy6WlWg2cQcYQ53I5t9KbX65y2Y3THcS81+rhET+8cfbwWGdgjdlhO6NGlj1F7B10oN50IMccdqBsOEWttHrWy1cU5OqFN0lbe7tU9H62o030ETXMyUGDbHtr8+MXBDxpDw+P9RPeOHt4NIAwqC8HCxOBJFNqbNV1DvhpyERVNtogLUcdfqjkkmrAk3k1zoulpyLSp8YYF7tUqTqDzq9P4TkzlY2B5t0zBnu8/iqVn2738Igf3jh7eDQCtVPY2nQ6qYaZ1dX1LTlTyZqUq6GccMw+MqW9Ta+zsmJFr/zs0sslm2lzBj2fSTvPube3101p22IwDDRT2uN1WtvDwyN++NbvMTExLjYhUU85Xf/kic+qakFVKtWaGl01xlq89nTCvXs+8rD9pFjqk2znVFmw+A55uafsdgljOdn/u/AL7iciE8m0tLV3yG67/4ssXDhfjXZCKuX6u2fnmbvUUfim6+ExmTHhW7gtTmFRjXkeduRe3CFKEzAdafFgaPpmB3tPafRsypGpUcJwz6xNABwtf8A5cdAyOQ93H3Bcu0B+q0ONb4I1gDpvRitw3urweTQvAOOHurXrwTrXJLmsllWq6umqB51SrzjMSE7aJK/3OrTIxx25m0yb1Sb9mmp5f04uvvxGt2HJru/cSS7+4Q/k6nlXSVENeyHQOtN/7z/peLnkRxdJJhlItVoVdcCFt8/45KVKUfOvSTqZEX1Ez+sruw3UOTA9bDREvXfj2z77Gi59s4PJHiCLfD7vjq0qA/Qt1PWvLlur/+GeaWaABvwyswK/nEObIxjumWYGaEKPYHEmj2i6uAJ82tcMptucW11MZkx444ySUGkcrcKoPFMeU6w4Q6FQGOzEMJbEmdEcmrbZwQwG9I1vAH1bBdxIMLkSyB9YvsjdGi9xICrz6LPrGsg3OgAhf5O1dZJxBjC0TqFPndfTUMfugyoNdblgsAkJLWuhZ6XMmZGXww7dTwL19qvJvCy55S5ZsPCX8vvfPSQf+9jH5Mijj5K+YpkZcll8w01uMdjV865UhtUI6wCELINQvXLNNJ/Lr65zja9Uqi49U+MAebG4jPfV1pE3Ekyf4Jlr5G96MDRtHAH6Vt8c7Ztwux7umWYGaCBTeKbOjXfQKvoEFgdGy8I5GO6ZZgboUAc2GLC4oeniCug2RxDtY6zPn8yo1/AEBhVmikplEUx5LT5OoDjWYI2uKU7Uo4kL0BxOaTlag2oE1gCMT+MVQINgsPvWmOzZRgAPUZ6MvnVScYM6NNrUrdE0PleXoK5rg0Wqi0A6p0yRSi2Q4485RKZPUcNa6JGenh7545//Jp/6wpfkmBNO1EcT0pHPqqFVTzs/Relk5C9/e1wkm5ZuNe74zCw7I0CnrW2Kox3oJUfKyC9hISvO8S77+vqasqAsyi/BZNGMuh0NbCACbQZHJnfTi7iBUYRX6t4MhbVxK1vcsDrmSLBBqdVNnDCawOghD9O1uGFyJpjOcaQsrejfxxITnjtTVDoiGi8VZo3YOtY4AzTa29tf0VlQHmvMwz3TzACtKF2TAcaLMNwzaxOiDcDOrZEiczMAFjc0/XB5rk0wPsgL3qyjgGfOh3ummYE6hHaULnVNnVP3arL4cEoFoP/VWoZsz6np+KtmTErlkmRTSZmaEzn+8IOlM5eU3u4u+e2D/yfnf/xzMnOzLaSkxpvhFd9Hv/j8i9LV1Sebb7WN1MpVmTqlUyrlfs0jJTX1kilFuVR1ZUPUmUy9jgFlpLzUBeUzw9JIQPbA6pdr0zEw3DPNDG1tbYN0kDvloA6sHEPTNzswnWx6ZlPqlAH+0f2h6ZsdoAd9aFtdmOxbof82AIE2fEd5b0X/Bl3qwNohMF2c7EgooxOaU4rf3d0tf/vb32TLLbd0cWaozXDHCWg8/vjjsu2227praNMpokx0IpQjTjzxxBMya9Ys1xkjC2vA1qgbpU8DASZHaJA3/L3wwgsubuONN3aGClrRdMAa1LrCOkPjw4xyf3+/LF26VLbeemsXHxegj0zhzzYJAVbnmVx9A5IkK7wUQagezaDKqXFPZ6SnVJFqeop0lxJyzPvPkKCmAw2V6/FHHSKnnHyIZBMVCYuBLHvxJfnMpz4tf/v7X2XRNVfJxpvMlEKhz/G5YkWXOthZ6e+ryA9/+EM5YP99lP7WjhZl23XXXV1d2eCBzpxrq4d1Bc9bR4luP//8804es2fPbol+Q4OAvjF1//LLL7t2TrkIlClOoL9MZ8Pno48+6uqcc+LRQ9P3uEBfgt6hb7Qz6hXa1HHcvAPoLFu2zNGkn0H/rZ23ov5XrFjh6L/jHe9w9Q1djpTHricrJrxxBsuXL5c//OEPsuGGG7qGROdBQLHMWMUFGs5TTz0lm2++ubtGWWxDCTNscaKrq0umTZvmGir0UFqOxnujZbB8AfmhLjRQOgk6SkBHbe85rdECymLGbF1BHtYJGG+Wr/EeN6BnBs+ayzPPPCNbbLWl9CvfDD+SA2IOta/gm+dgoM9IqDedSOnIv2OavLyyR3555/1yy533SF9fKNM68/LVL31UFl75M/nZ9/5LveJAtttmO/n2d/5TNtp8I324rA20Kg/+7gG584671ahrp5jMya233irvePtbZcqUDvc70Riuj3zkI4N1RR3QDqLlXVdYnQPye+mll5w8aGsMChrVr9EAGkzbo2N01JtssomjbQPCOEH+0Ono6HAD4a222srFo5PoYNzGAfnTxzz55JNO5uZFWnujbHGCmQtkDp/Qhy7nBNpE3PzD46pVq2TnnXd2tJCH0bS+YLJiwhtnlJMR9bPPPivbb7+9q7xWgpHtQw89JG9729ucotCYabitKsf//d//yUYbbSRTp05119BtpsLCi6kI+VqjhM/nnnvOxW+66aaDcaS1DtsaU7NAvmb4mS158cUXXZ23Alan8Ek5HnzwQdnhbTtKOotxwBOudxhhQuWlxtnehqZE76vF1v9SVjEu6xU59NgPSHch5+6ffvJhctrx+8kcveTnJE877QNy2RVz5cvf+Jpc8NELJKcGu6+nWzrbpkqtqvkpvaOOPl7OO/dM2WOv3TWHpHu/jPGgXMifMtKJN6PzIi+D1Tl5zpkzx+VPXNyADmHlypVutuaNb3xjS+gakAE8/+53vxts5+gCso7bOFkd/vnPf3btjEEK1+hjs9vXcKB/ZbYEmptttpmL47xVoI0zIHzrW986EFOfzSEgA4z3ZMWEH3aYt0ADskpjREscsLi4Ap0gIzvKEW0o0DfDFmdgehdAn0CDJR7azaBPQ6QjJJA3wTpGBiYEMPQ+gWeHy3NtQpQP8jY+AbwPTd/sAG3TJUAdQ586z2XrBnZ41Ac0POneSlfVC66UZOYUkeOOPkzKNbzrvMy/9pdSVvvnfjlSveSfX/IjOezwA+Uzn/yEdoovS1d3n3bI0yVgD246Rc3W+K/nXp+9AcgHmeNZUS/D8bO2IVqXtDE8crwnZEL8cM80M9CWoW2Ba6PbDP0eKRifyJYBobUxw3DPNDPAM2ARIfzaoMDqZGj6Zgd0iSNyB0YTXYj2uXEFG2RCizIQx7X1BZMZE944U0lmFO0YbUAc4wwABbJrlCdanmjaOILRANAGXNOImkV/OBAPDcKa0jQa4CFKI8pjq+QLOELb4s0gAhpRvVRRUF7uDLwjU8Obz6iBK1bk2CNZud2pt1PqDZZk0XV3S6BJSzU1eomibPv6begF5Z777pMpndPUdVM5J3RApHHQCYKa2yrUQEcNouWmfM2Qj8kbmEGwczDcM80MtGUnP6VrtA2tqH9oRusdDI2LMxiisrf4oWnjCAZkHaVPeQhD0zc7ABsgWb9ubXKy45Xa7uHhMWrQdUQbUNRAW7fm0minltSOpVouSWc+IzOnimy//XbqCZQknW2Ty+ZeLS8t69PznJsOv+e+uxlhyi7v3rWeqctMKQ1malPN8TffqHEeTxiv5fLwaBa8cfbwaAJCM5zapBKhGmOOGipV9bD0X1jlnXxKKqWCa3SnnXSMTO3MqZEJZPmqLrluyS1SkbR8/LOfkf+993dyysknySYbzXL2GDO0On/eK9enc/XPQJyHh8dkgzfOHh5NAgaURV3YUY40Lowo229WK+oTqwddU++50leVd71lAznkgN2kXOqSjHrTl161QDbZ9g0y98pF8pWvfE1+8oMfSSal+QwYZXYXI1MWmznoAMCFMYD3Wj084oc3zh4eDQAjjDdrn045qNHEe06otc5m2HKyKqlcXuNF2jo7pS2bUCMtcsrxh8icmW1SqhSku1CTT33+q/Lkk8/Leed9XGrqafO70M4gJzX/gQDIu950o0Q9PDwmE7xx9vBYZwzsHT4w+TxooHGhuVBbGmhIsnApmdYU9QQZNsWulmSTDUWOOHJfyeUTEqTbZO6Cm2RVH6+b05JmAZjU9JmyGueKZlclu9UI1a0eIwfWFup4eHjEB2+cPTwaBKaqbif5O2C46k6vVKuhJNMJqQQ1jUhJjU/PgrLMaM+4T8FOPvFQSWfUBNdC6Sum5KoFv5KeXpF0KiHl/m59pqxZqYHGg3YZs3KdVcrMebsIDw+PSQhvnD081hmrm88/2cmBiExWvWJeOmvaSqUmqVwb38VIuVyQae05t8nI2aefItl8XgpBKJddfa1bsV3or0q2vV2zwd82o7+annv37I2zh8ekhTfOHuMMTN4OFwxmkVDd8aC+9XKoL+vCYLGYlVbnli8y8+o5M5XNhg7uZiIpuWyb5PXujGRSDttnb8l3pCXMp+Xl3l75yeVLJNumGVSYME9LrZyUTCKvZxh6NfBp9aI1lNRo173p+DBep7D91LrHZMd46N08PNYeY7RS+dWAqRg0F3ahIXJahzupW3BOw3Ioc6am5YhDD1RDW5JMe16uvWmJLO/mjTPGnB9x4RvpUKqV+mYQxVJJajV2bIoOWuKB/87Zw2Ns4I2zh8cYIpmpT1qfdPSBkg/LktUWuXJVt1x5zY1STrGHshpk9a4TbnGYptS4IExJJoVPbUvMPDw8Jhu8cfbwGCNglHm/XFUHeKY6yWeceIwE5YLGJWTuohtlZZ9IKUipMWaPYxaCsUu3Ot+prBrn9MDPVMbvPQ+F91o9POKHN84eHmMJdX3xnVNVkVOPOFimtmXcLw+9sLwgc6+9U1IZPOUBM56oStlZ54z7DlpYAe7h4TEp4Y2zh8cYArObSgbSmRbpTIkcd9ghbs/tXOd0ueSKRfJSt6ZI5qQaMr+tdlmNOT8EUCvzW8L1PFoNvxjLwyN+eOPsMTFh21hOaPCzoiXJqIkOykVpU+N76okHsj5b7yRlVV9JFlx3sxTVPlcH3i9jFzm6XwgaZ4viPDw8mgffuj08xhBpNchBWHXvkFkM1pET+cApJ0mx2C9tHVPksnkLZFVB0yTS6j0HbmOTRFCTdDorIduPeXh4TEp44+zhMUZIqH/M59BBteyuebXMz8cff9QeMl2tdK1SkuXdRbnymps0ZUb6CiVNq2nSSamxRWhKLXnM3rP/ztnDY2zgjbOHxxiiVO6XfEZNshobjHNF7XROLfb7jztUqpV+aZ8yQy65fL68uLJfOtunabpQAvWcAzXO6kdj4WOF/87Zw2Ns4I2zx8TEJHnfyq5htVog1WogKbYTCypucdhx6j1vOC0vhUJB+guBXDX/RmHbkUw6ITVNk8impRzEv0OYh4fH2MAbZw+PMYM2vyChRjkryXRG+Mnn9nxGPeNQOnN4z0dIWi12mMjI4htvk5WrRIrlwP2QRrFUlkxmbJqv91o9POKHN84eHmOIRBJjnHCfR6XVY05KVbLJmuTUiz78oL1kA7XSGU3z0su9cr0a6IQa5DClCdnS09tID49JC2+cPTzGDGqKKxjodP1XpoTp7bIkgoqo6ZUNpyXk4AP3l5TeymQ65ReXz5fekgjLxxKppJSrLpOWwy/G8vCIH944e3iMIUK3PlsklUpIsdgrmTS/1RxKLSipNy1y9hkHSj6TlXxuiixb3itXL7re/eRkb6FfcvVHPTw8JiG8cfaYmJgEm5AwK/29731PpkzfUFLqPU+ZMk3eusOO8qMf/UTakjlJqFud1UQnH3eYlMp9ksjl5NKrrpNkdopks/yA5GqQF5t51me66154PdTjLETjPTw8xi8mvHFmcQq7JfFTepVKRWq1mnt/16qpN+hn+BRG0d3d7Y6gVYtmorxCk2uOBGTRKMjPYPlbnNGxc6NtWDf6qOTqUKtBg8+MLP86bfcjEHz02wJEebI6ps6j8a8Gk0G5XHb6aedg7332lk9+4uPy7W9/Q4rVfilVyjJro83lQ+d8XH7yw5/J1FRGOlUMJxyzh0ydkZSKetfPrqxIKTFNMsmUZt6vFVTVcohbyd1bqelR6ydUuVQKer8uH0qgfriUQ20fmiIUjWc70GDk8qNb0XrkHL6r1eogP3EDmoScDk5o59BuFdA5ZFAqlSTNogAFZWEVfStgbQ1Z08+Z/Eeje80AdOCfQFmidV4sFgfO4oP1bfBtsDpplQzGChPeOFNRdHZUFJ+l0IBaXXE0VJRn6tSpg0pMJ9KKMkDDFNcGKZSB4LZ4bBCWB3QI0XyhRQBG09IBu9cIoGV5k5/Rtk4qbkADutYhUMfQHm3nbOXFmNsgjvyuvPJKueO22+WjH/uInH76aS5vlaJcOW+BbLzZ5jJ/3kJJalSiVpaOXCDHHH2IpHMJae+cIU8+/ZKUqjXJqPFmH27QW6hKLqPycQMa1Qfyq3JPBzQuhfLiaKwdhsq9Xs46X8ZP3LA23dfX5wwz51aeuAEddICBAYaJvgb5tre3D6SIF8YnMjBdtDK1YpCC3kOHMLTO8/n8wFl8gF94N54pD0dgujhZ0RoNjxFWeQAFovKsI20FTGkNjLChTwNuxciSxoIMADTpPCgD5WqGDGgI1higQ57GnzVazk3mVhau7blGQJ7QgCfrGAF0WmEcqEPjjzIYqHPKNRKs/CYn8iOOX5761Kc+Jed/+DwplUuSSqSkv1yQGdOnuOcefPBBKfYVnAyzmaScdNx+MqNTO0M8Yo275fa71RvWwVFWPfhETdOk3AYmiKdSVG9L81MhaU5aL+ovo6GaWs+zLkjIvZH1w+rRys8AGLljqKLyiAtGlzIgt7a2tsHyEOIGtPr7+53uwTv1bjreivZtfEKbMlgboFzW78UJeIU2gDZ07bwV/EMDWsgAXYzKn/jJjAlvnKkg66itE7XKa0XnAd2enp5BA40S0WigTUcSN6yjgndrSIzyKY81pEZBPtG8OCd/6NhU49D70etGEKUFb9CCV3huFo01gTqkLqlTaALKQ52PZnCAPvIsaSk73gZGZo899pCvf/3rstUWW0oi0DpUI5pK8hMYalxLRWnvaJN8Z5uk9Tlmn9tVpc869f0SlvokFQZy7+8eluW9FSmoHcY3TmueqYQack3X3tEhpaIOEp14VH6aIqmG2IVQDTLxazFuo7zwjNwxysjB6qQVQG4E6oE6R56tMEyAGZIOlSe619XV5eiafrfCczQ+ja61AWD6GDfQYXQA2hzRAeJawT86xiyFtTX6e5tab5UOjBUSWuHx93AxY9myZfLAAw/ItGnT3NQXHQcKbEoUJ8ifDhyaK1eulJkzZ7qRNkrc29sbu4GGDjTglVEmCgvv1qDoUBsBDZC8TI7kCWgwL730kruePXu24xmYOhFPORodXZMHeZpxoEOiTDRWOs641RcaeLnQgWd0bcaMGU4e3KNcawLPUVbSU0eUnTiueZb6KqgxVuuqHVGb3H7rHfLlf/ui/L8vfF522WUXSahHvOSWO+Q/v/VfIp0byrt23UdeXrFSOqa0y4bTc3LXNb9QIhX51a/ukVoR7wJZqTFNVSWjlrqvj3fkWsZQO7eQ6WHt0NhdTZ8R9bix1Zj3VwNlN6PMlD71aXW7atWq2PUbg0A7wkAiO9oYHTbtnPLE7T3BJ7SsjRPgnzj6G9P7uIDsobN06VJ3hLbVwZQpU9wgMU5Yf4LOEuCXuuAcGVA/cYI6h+Y+++wzWA76ADvnOFkx4Y0zykuDfeaZZ+Qtb3mLqyzirNNEiePG3XffLe95z3tcR4Y4od+qUd0jjzwim2666WDDNb4pA2hUeemUrUMC8Idhgdfnn3/exW2yySb/lI40pCVdIxjKh+WLF/Pcc8/Jm9/8ZhcfN6xDgD94ve+++2S33XYbuLtm8CzPmW5gXPACkU2xvyDtnR1uQddPf/YzOeeMM+V9Bx0o1127yMmzosY2kUo789mvdujOux+SL3z5m9Kvhnba9Ha5+bofSVrzn65pktqS+11+6u3X1FCHOpDh0ywKEag+UjfW2q1Z2PFVQHnhG7kD2hm8oHON6tZoYPQBg0HCm970Jieb6L24QF2bDt92222y5557OrrWvk3f4wI6Q/jzn//sZM7AEKBT1EncxhE6VudbbbXVYBxoRR/38ssvu3a+4447DrYf0Kr+dSyx5mH/BACNk4ZKsIZqDcY6xDgDsOkuEO0whkvf7MDolSM04ZfOhACIG5p+bYPJNSpjAnzi0RCM52g65NEM+ZMnML7IkzjuGe9xB2A8A3ijzsFw6aOBDpTA8yYTrungkJObgi5V5Itf/LIa5rNk3/32kRtuuE4935RUlZ4zyuop9a3qlimqYgftvaMaXHYJy8vynpr8+OfXS1LzLRTU+05oZ61pXP0ntT7S6qVTRua3a5qT9qmcElj0HqrxHq7M0WDyt3ql3GYYkMdwzzQzREFZTLdBK9q3GWZ4xoOL6jZe+3DPNDMY0HXkDf/EUwYM89D0zQ7QgSbeelT/TReGe6aZwRbeUQZ0DtoEi5vMmPDGmQpEUayxoDDAOkGOcQbA1Avn1ng5t0YUTRtHwAuDJoAenQmBe5RhaPq1DdY5I0trINAjPhqIi6YBNKLh8lybYDwYX/AIoAfvQ9M3O0DPygBN6phz6hxE0w4X0Ec6UY7kY/JkapBp8ap60EcefoR85ctfltPPOksWL17sPN5KtaRGF9lqZ5RMyIzpnRKUipJU9d5mq83c++lqLSMLFt0q3X0imVxeyoU+SedYf6HlVtrUgkrOBS0MF3WouiRS2jY4Jtaso4BO2eoUwEMz6nY0wfSKYO2MOmlF2yIYLcrB7BSwQUkr9A9a0CagM7QBZEE8YbhnmhnQW+oaI0m9cw19ysP1cM80M9gAiDJAD9rEcUQWkxkT3jhTgVQeSkNlUYEojjWoVsBGcigw5QFWjrgBnwRgsrDzZiovvMCnydbijEeTt6VpFuDBZAqN6LmVI07AC3UJoG0jeavzkWDTjnSkxgt5mrE57LDDZMmSJfLtb35LfvSD79c7Y6ymgw529DpHPVaYBlf56q2+rpXOUGRz7dLdHci8ebc7xzjb3ibFUq96y6GUKkxrQ5dskBl5aiI2b+Fds2inhys9ApCx8Q8oP2U3PuIGdIwWg5toeYiPG0bD6IPR1n0zYLSgbwtcOUcG0XqJC9BHBtS5XVu9t0r+0XYPbdpUK2iPNeJvXR4e6zGsU8Mw07nTuZhxO/fcc+XmW291q7bPPfsc1xizaVZnM32XkXJNB5zaATtj7SytGlPtk7LqGR+0/95SVM9bEjm5+urrpasQqKlVI5bJSjksSz6TZn8S5ywPDmHUMCeSWGtnsQfCmtGKAdC6YLyWy8OjWfDG2cMjZtjIn2De3/z58+WHP/yhnPaBU+QTn/iY21O7xqtivBLShbzHx6CrhdX0NV4S4/Wqxa3WSvLWN24rW206xzXgUi2USy67Wn1hNeSpvPT09ks1qKmBrtMHIVaaFWPOVNc9Zi2RO3p4eIw/eOPs4REj7B21BQwz05G/+c1v3P3LL79cDWr9fWKnBtKkklnJZfLyyJ/+5NK6OKY3md5WA5sIq5KqFeTM9x+j3vMqqVYrsvjmO2RlT1X6qwmZOmWWuB+HBs4oE0JnoEP1ljHKdcO8bs3fe60eHvHDG2cPjxjBN9IsYOF9oRlarr/61a+66e2e3l7p6e6RYrFPiv317SmrQahGtipvetMOkmEPT5BkMUwoVfWgE0n1oMur5MiD3iCv225j9bJ7ZXlPn1yxcImIeuAVvd3GSl7ekaq3Haphrumxbq5p8mk10oT431l6eHisG7xx9vCIEUxjs4CFlb0YY1tQw2IwrjHYHZ1tUujpkaqmxXj3qZEGvBHmlTW/UcHS6rIa7FCNNT8n2ZbWvDT6tFOOkEw2kLI25XkLb5QVXeqt6+N8PpXRBAnhxy7KmheLwIB675oW44yRXpcugDJ6eHjEC2+cPTxiRHRFLUYZw+Y85oGdnbp6ut03pG0dHZLOZfS8LB3tHRKEGFE1o2oH64u3U5LNtalpTUo2lZT2TCClvoLsvedOssGG+qwa++7+mlw1/zaZMoVX02rRE6wIYwetqhpncsM8pyXBvtrk72enPTzGLbxx9vCIEbY6m/e0HC2OrRcx1Ex75we2wKwUCs6jrtYCCfj0yr0XVkNbC92PY/DTmVXyCqpSq5RlekdO2lOBfPCM90uhVFATnJIrF1wvL63Uh9w2nWp9Q/bVJoDIfuscvHH28Bi38MbZY5zBTeYOEww2pYrqTgz1NY+ZI4h+u5rCiMKHesOZdvZvFucZd6Yz7o0wM8jJdP2b9ZS60BlNn3J3ko77dKUkR+z9Xpk9a5ok1PNe3l+RK675lYT88FSYVs87LUGlqmn1XEOp1KeZqjzrdntEjNcpbD+17jHZMTF6Nw+PoeDHGyYTsDUD9sZOhzM/CTWqiQHeuc/e2Zj3M047ScqlHsm05eWaxUvkpRUi5Srp2LAiI9VyWWphTdK5vPuOGtumY4ARMV5XZvsV4x6THd44e3hMWOCRp6VYqcgx+79HZk9rk1q5z+3DfNWiGyXIptUgs1MdQY053nsiI5Uan3XxPO6zy8jDw2OcwRtnD48JCuxquRa47T1Z/3XBuWdIslZ0n20tuO5GWVVggxLeOPOddH1HEp5JJpgWD0RqJbXYo5jbHgLvtXp4xA9vnD08JjDS/FSkHhOlohy+906yzRYbqQGuyIur+mTu1bdJLZ2WUsDWI/xYQ02qbhcyfcB9n1X/8tnDw2P8wRtnD48JjqBalhntebeX9nFHv0+y6YRkcx1y6dXXyLIuNcDJNjXXfJbFD5XUneWgUubrLJ52eawN/GIsD4/44Y2zx8TEOkzHTkZU1BXOplNSLfdJPhXKEYfsJhvNmu5WYnf1lmXhjbdIUdOF7sOslGvwOM2hW7HtPWcPj/EKb5w9PCYo8F9zapgTamRz2aykNIIfqDz79JMkqJXVw03Kz+culBVqnfkGGu85gSPNSu1sXmrDrgf38PAYD/DG2cMjZrADGHtmR+H20NZgvxFsm5RwtAVXPDcUNqVcT1fTZypqlBNSq7IpZ32meu89dpKNZ0+XXC4rfcWazJ1/k1Q0y6Qa42olYJtuqZTLemSR2Jq7AP+ds4fH2MAbZw+PGMGvUrHrFxuOmEG2PbXZjITNRfghDECaWo2FW6H7HIrnRgINmN3EyA8DzTfPHWp8Tz/5WCn0rpBEMivz5l8vXf315V+pTFLCaiDpbJv7qcmRYAOF8YbxWi4Pj2bBG2ePiYkJsgmJ7QbG502cE/D6MMi9vb3OGGOszUBzxEjzE5I8MxLYdxuDn3CfRykCPdfDoQe9Q7bZalMXVa0m5ReXXeW853RWpLuv232ClU61sUzMpfHw8Bhf8C3TwyNG8ItUGE88ZIBHjNfHr1Sxr7Z50FxjjElfKBRcWuJGQqimmB+1AOlUUhKhXlVrkteW/f7jjpByoV9qlUB++cs7pKsnlP5yTabOmCrlILHOH1J5r9XDI3544+zhETPMANv7ZZvixmtetWqVu4fHbJ4198FInnOoLjI/kpFMpevesxpNl4c+XipV5H0HvFve8JoteMEs3V1Fmb/oegmyKelXc57JpNzGJR4eHuMT3jh7eMSI+pRz/Wci8TiZrsYos9gLoz19+nSZP3++zJgxw3nKGGvS8dzInrMaefWcU2lNF+gzRTXm6tS6X2tOJ6QtLXLaScerF60xtYRcteB6WdHXLz2lgvOa1U6vE/xiLA+P+OGNs4dHjLCficSg4dUCpq2Z0sZA/+AHP5APfOADsskmmwy+f7YFZKNBmEy598YpfhGjVnVGGmRTCSmWqrL37m+SWTOmSzaTl55CSa5YdK205aYoHS2TS+nh4TEe4Y2zx8TEBNmEhHfIgCltM9QYZjzj7373u/LNb35T/vSnP8m0adNcWjPQo32vS5aB/mNhWDqH8U/oeVr/qpeu153qHZ/zgROlVK7/3vPlC26Ul4t48/XPruoGms0966u561QppwZ3gR/Oaf04eM/DwyNWTArjbJ0eHSCdGh1cK6fezMvBI4JuKxfMQNvoW8cObGq0UUR5sbxNttAjAIuzNGDd5AAvq0O1iqFanXcN71ABy6N0LpsCeIFHW6w1Ws8W8CxT2ASD6clDDz0kW265pZOjvXceqkPoNXF2JAA9Uw85LYW+/rq4MikJtFwVrQJ+SDJZqkiHxh+8346yxZZzpFBLyLK+vMxdcIfbsKRWUV7CshTVcLNBCZLtK2teGN9yiQ+t3YYlFa3ish65XwvVxEOL/bqr8es5crDA4AUZogdrI/9GQL1Am6O9ZjC9j9ZRXIAOQDes3kF0sBcnjEejTZ9icVa2OAGPJn9DM/q1iYDWaHiMoKJQHFbD0nhptDRgKhQFjhsoD9+yQqutrc1dU6ZWdR4YC/sMh47dDAAysWnURhDtECxvZEvgHsGuwVAD1CjMWAHyNp7g2Qxl3KAuqVPqljqmrqnz0XSOdCqUnzxMTnxCBS8XXHDBYIfPu2gzPqSPyhHdJh/ieJ6FYsTxu8yUobNDPXF0QK+xl9WaGlrty/K5jITVAjZbTjjuSPWss0pjqixYuFiWrSpKmhXkCR04pJNSrFbU+IZ1WoE+jMwzSTdLzldaGOk6t/VvsZWwJLHw9WqPDVHZITd4N11rBaw+QE9Pz6BxQg9HU/+NAtrQMx3knDjot6KPgRb6bnIf2h7jBu3D2oXBzlvRv48lJrxxNiWlw+AdHhVGozEFjhvQoWM1QJuyoMg0prgxdepUp7zQgy40OboOtAkgX3iyYNfwTUdO4Dx6L5q2GTB+jDfyhWd4jxvWIUIXngzUuXVSa4J1JJYHz7S3tzvjjqEnmN4y4LAV2qSDtn16RUDPuWYKnHPKk9FjRb3cVEZ1QD1pvNpspt6hO29L6wfDevj73iUbz5wuyVpJerq6ZdF1NzlPmgVlySQrvNl3W9tMQg16oGVOa1DDXeNnJdmoW/OD20wmp7fyGqVXLbCRyMV4J/BKANkQ14r2hYyhQz1OmTLFHa3eW2EcjFejbXpI4LwVwEDSzikHgC66FW0PccEGZENpWR1MZiRU4K0bhsaEpUuXyiOPPCIbbbTR4AiPhkyj4hgnGAA8/vjjst1227nGSgNCkSiDNaY4sXz5crfil8ZjnQiKSxmsA28E8AcPJlPrLGiwzz//vEvDYibkbvegyTllabQDNR44kjdloUzImpXNG2644UDKeGB1CD+UgXNk/be//U223XbbEfkzGZgckRMdLUeuMcwzZ86U888/X+6++2757W9/6zo+aPEMx3vuuUfuuusuF7/BBhvIggUL5F3vepfjvae3X6ZNnyIf+fD5ktU6KZUDqajnq1qgHrUa/t4udaGnyvJSRu57+C9y2dXXq8Wpysx2kX//wkekPVtRY6tdQJDXXpcdxjC6Vcmk2RilJEk10nyqVVY2McwrX17hZLHBjGn1ul7nr6XXDugbA5OVK1cO6huyiRvwCL/Qp85f+9rXuvqEPvXD/TgBDeg/99xzru4ZlFqbhv9G2/dIQH9pZ9CBPjoL4Bv6cfPP4kj6uF133dXJgXJAk3JZ3UxWTHjjTPFRHgzk1ltvPag0BBpR3A0YetC2RhsdYTbDOI2Ep59+2nXueGMoKo0Z0JGbLBqBNQhAXnZNJ0GHATbddNNBgwLNaHqTxbqCvKAJPYA8yRPPc9myZbLFFlu4+LhgRhVQDgYFxP31r391xpm4NSH6DF4yxoWjDaaQEQb6qKOOkl//+tfy5JNPOu+QeOhiFJDzyy+/POip/dd//Zfsv//+8oY3vMHdRw777ruvM17adbm8SavSVyOrBiSdk+6i1lumTU4+8yPyj2eel/a2nJxw7CFyygnvk2S1XzKBDgSYw9aQyqhpT1akFlCnOjBSU1+psKNYuyxbutLxtOEGM7QkSi3mhXm0IXQAeXR3dzv5bb755i4uWjdxwXSY42OPPebauek4src6iQvQQt7PPvusa+foTlTnrK3FBeTb1dXlygF9qwuuqZu45U99o98MRgH0jbbJZrJiwhtnlIN3QRipN77xja7SqDDYMmMZJ6BPp/qe97zHNVZoEse5KXKcYEERBorvZOHbeIc2smgU5GMNwI7wx/lTTz3lrlnQBE2jZyrFsRn8Q498jDcCjZY633HHHQdSxQOrQzwl+MMgcH7ffffJe9/73hFljD7wDIMXe/0AH+RLx45+8u58zz33dF4zHVF0NoDnoGF0SHvsscfKJz7xCUcfWD5V9ZidnNQohwPlpiZ6C2Xt1PNS0otrl/xGvvXfP5G+sqinnZLrF/xY5qgXndE+NqtVpY+5d8zlUL1vNbwJUfpqnoOa3gzT8tTTL7l8N91kjvKl+hCveg/KH7kxQHnppZdk++23d/Kwe3HD9I/ZCzw4ymIDoLj7F2hB/89//rMbBNPOjWfiR9K/RoGMaeccX/Oa1zjanBPQ67ixYsUK18532GEHJwuDtaFW1P9YYcJzRuVQaQQqjAA4ojx2L65A47AOFFAeK8Nw6eMI0LNGY56lKe3QtGsbjB/jCVgcnQPB6BssPXHD5bk2AVg+8GYNkvyHpo0rgCiP0TofLn00mGfFszyDYYcPrhnAkS/vr0lLHAGZkpZ01vlzDe94Tui1pQuqNfWOM1IsqQFx+2vzLlLThjpI1FBRT7hdDTM/dpHXKjxkn3fLjI42jU9LsZaTBdfeIbzl1qxRFg01qerzTI2X9Hl+A1pLr/TURCtNylSvc02r+Q3lt9kBngFygm+THRgufbMDgDaBuqQM1tYp23DPNDMY38yuWDmAtbvhnmlmGNSzgXYHoMv5cOmbHawPt7Zv/IPo+WTE6h51goKKs0ZilcU54DruAC06WZSIqVaUlg6VMtGIh3ummcF4tSP0rRFZA24kWL7wQ+dkDYQAf1Eeo2kAz9q9dQ3wAKJ8RXke7plmBviDH+oU+tQxdU2dj4Y+xtRWleM58w6N5+HLjDXgCB3uQRNa1jFxbdP6pCNPOutUoi6Tvt5+LZ+Wc6Cvcs/qM9RFSo0qq68zKe3gCkVpV1t/5gfeL2nNr6dQlUsvv1a6e/UhfRaDLomKJDVtJqVeUYKBgebLt1Tusyk6Zc1fPWZo1LTDHI7nZgaTAbJB5sDqP6p7cQXgeNX6itLHWNjgKs5g+mG6QRxloQyUa2j6ZgfrQ9B/4xtAm+uh6ZsdzChDj/oGXAPuT2ZMeONMpRGoMCrLFIZjKwAtUxbe+xr9VsFocbTGajBlbgSWH3nTOXAcTrbERdOAZsghysNQHpuR/2gBLXikjoHp20ggHR2cGRlgsiJgrLnG4AIMNoh63IB8OMdIc8/i9Y563ryH1DLqlXZp6kHX77m0+hwGWqplybGKu1yTg/Z5l2wwY6p61B3S21eTq+ff4Qw7yQrlblF/XwqVguakEaEOStLwrHm68jPNqkZZL1NMa7cI8AvfJjuTZSsALfTQ6obzZrSt0cAGBDbgB/CPPrUC8Gm6hr7bAAGs1sH4MBwtytTK+h8rxC9dD4/1GIz8WeCFYTEvgI6FRYwYTzo7Ot7777/fdURz5sxxRwYBDz744EAuI8O85qGgU3PfLfNNshrodCKQvDrEp59ykvT39er9jFx19bXSVai5jUgSWTVCQUXaMm1qhKMdoHYV0HALwDS8Cr1WYX3onD3Wb3jj7OERIzC+rKI2zwdjSeA9M8aa7zjtfTKBOAwPgUUwo4JbuPVKqJnVwFKu+gBBLb6eMTBQr1ft2iEHvEG225rfew7VGAfy80uvcEu/Uqk26ekvSEW94xwfTWMDNdTcCVBaSc4x0GNsoT08JjG8cfbwiBEYWZvSZooyOjULmNZ2n0CpgeQ9Mu+0MaY2hbomuM+YBuzjPzfk1THQc+kyTIUyLR0Kk+inHHeYlEtdWqaSLL75dlneWxJ1oGVG52y1xjqQ4GGe0xC6oMbdPGcPD49Y4Y2zh0eMsHd2TFXz+RceNOf2zhJDbJuSYKiZzsaY857aDPhoQeqE+7s6YEbJL2CKOpFy09bpZCBqj+Xg/d4sr9tujlTCflnRW5R5C2+WMNWu12nJZ/MSVlh4VDfMNTXKNQy1As+7jrUrn4eHx+jhW5eHR4zAG8bQ4hnzjSrGGE8ZA00cRzxbjDJpnZerwFCPGmotNbeBC3zj1c0aQ5pOqXHW83JlYKVtoia5VEU6dHxw6slHSibLd80JuXLBTbKqS7R8mkg9aBxtNvh0b6Pxmt3TRsd3HR4eccK3MA+PGIGRJdgnMRhnDDGG2d4/Y6CZxiadrdIG9syaMOjEKnBso9dAsx44SamB5YImX5N2tucs9cnee71Tpm/YJqlsh3QXknL1/Ntlaqfmwxds7KmdoDw6uEgSER0A/DMtDw+P5sEbZw+PGIExxhvG8JoBxhhHDXP0HTRT0DxDvH1G8+qw5vvqzZjNRzCy/LhFJos3zqdW6hIHNZmSywgfSZ1zxqlSKhfdp8xXLFgsL6+MGN4E3nZ9wMBb6CCRdNPcHh4e8cIbZw+PGIGxxdASbCORoeAe6QBG2s6Hg017W54JtysYzbjelLGbFojJpJP1zUowygO7fQmrspN5yUha0uqpH7HnrjJ71lRJ5ZOyvK8gly/8tT6oxjjgOex4SbJE6FWgljmVaXO/8axjiDEDvHt4TGbUW7SHh8ekw/DmiyZfD5jrfAoTLXLWaSdJtdgrmba8XHPjTfLiCvWX1TiTDuNeqZalpgMDZ5jVG8c2tmgfjmFhgxQPj8kKb5w9PNZTOPOmPUCpFMhR++8ss6a1S1Dpl97+XrnqmpskyCTUU1bjnMy6PUwSQShJ9erZdYzNwRJ69PDwiAfeOHt4rMco12qSzWk3UBX56NlnSLJWlGKlKFdff5OsLOI916ezM+ph89a5ap9k8XCtFHk57eHh0Ux44+zhsR4jmaob2kSpIkfu+w7ZevNZEoYVeXFVl1y+8FaRlHrKtaSzwWwRWlHj7BavBfVFaxhsDw+P5sMbZw+P9RiYV37IYnp7RkJ1hE88+nDJZkJJtbXJpVcvkmXdOMp5qah1thXmvO8NqmW94d1mD4+44I2zh8d6jHKtKDn1nmulqmRTIocdsqtsPGuGM8DdvSVZcMPtUtR0QSKjhjwhKQxyWP/JQjYq8fDwiAfeOHt4rLcInGHGyqYyabfoi4+9zjz9RL2lnnEqLT+//GpZ0eteSUslqEqoIRkEmj7Hkum66+3h4dF0jHvjHP0BADZnMHDOLkvAtkEkWPpo2jjBLk58l8qRbRrZghHY9F/ciP7eKvTYYcrkMZodpkYCPAH4Il/LG9g1IM6uTQb2bCOgPskb3qJ1HuU7TkDX6NhWnNE6bwWiuowsKE+0XTSCQI2t+6p6QFUx0Afs+Q7ZZNY0yeqNPiVz+YJb3TYkyWRW2jLqZVcKA/ttq1zCeOsAmcNzoVBw17YxSzN0a7Qw3YM2dd7T0zPYBloFysC+7NE+phX6R3uDV2uDJotWyR+ejV+A3lMG03/ODZTL2orFR48WoulAtC1ZvO3UB5+WB7LgvulidDe/OBB/79YgrBEgGBMuoIOyThMB2n0aULRDjxvQ4wcNOGIw+NF8q8RWKDAN1BQWeVAGU7BX2/RibYAcUULyJUCH/KON1vjlnqXjGau7RgAPRhODaGWA52ijigvUofFL3UI/WuetAHKkbpEpvHONLBrln9phmjpgflqbEhuLpDR/frHq9PcfL4WuVVKqBXLF/GukoP0Q2lzs75N8NiOJZFqCZKaeSYyAV3hG9vBrMrCf4Iwb0EP2NhijzvmhEmi3anBmBsLaObvMoZPNaN8jAd6tjwFWHxxbIX9+UhV5Uw/Qo/1BmyMgjoABJ87iSYPcrA+Olpu65Mge9zyHHPk1OEsLv+gX98nPaNizgOeIixPj3jibsFESAkDIBpSUhoswo/EmxLiB0rJXMhUarSzot6IMNFToGG1kZDJrBsgPpTXZI2+U1OgQOCeOe2DoM42CvKHDEcArPLfCOA6tR2hT19R5o8ZxNECnox0MgTjK1Az5phN4wjqw0qxCxMu0tR4OP+A9st1Wmzq5l2sJ+ekl1yhdkbZsm1S1oyxUtLNSLzru4S91bEaQ86huN0u/1gT6FQyD1QEdtvUzrTCO0LV2RqDe0QHKZO0hbkCXPha+o/1MtL+NC9a/UQboGc9cA64pC0dCtIyk4R79EoF7HK2v5jfVbZBHeyat5UXb5j73rC9jxoR4ZEGZ4u5/4tfuBoFwTAlMcIZoZSE0hEgwbyuaNi5QuVZZphxW3lYA+aCE0IZ3aJvicq8ZsMZhSmr500EQgDUE0nDOM82A8UDe8Bal1yz+RgOrV+QMbzYgbBXgFbqUgQ7GrhsHctX8OcMRZh9udaE7tOmccsIxUqkWpBrU5IbFN0tvP95zQvJtHe4d9OqJwXgBn/BsOg7sGDeQN7I2naZDpizoYytgOg5N45kyoX/ExQ3jFZrQj/aprZABfXlXV9cgLdMBK4fFUzfIijC0jNwjcE49Uoe0XYw0cfBm7YprG3RhU8iPa2hOnTrVPY83T34M1OLEuDfOAMGYknJEkFYBCIt3AKaoXJugOcYNysEUp9HlmqOFuIECQQelIkAfeRFHmRoFcozmg1KTv9El2MAoaqx4xuqkEcATeRPgzXhED6AbN4xHgtUtvFHnXMcNaCBXkyX0kYG1g8ZAPirTlOYPj/oPWuz+VemvySHqPb9mizlSKfdLX39Z5i+8SSqavqCediqtnZrmEPfwCL7pCIF50IA6QCfihnXOgKlMymJyb4Z+jwTqgzJQ59bODI3X/8iAX+jDO/TQR4INkuMG083wbrxCm2tgcciFOMrI0dol5bayU1dWbuwFcjTPF10inckaPSOOejf+Td+g2dnZ6fLDs44T4944IxwEY0JHOKYkBtKYJ8M9KssEHTeobN6JQNPKRnkoX7SMcQG+kY/JxGg2q+MyuUfzg2cUFxkTOI82VtLyjDWiRmGNApCvyRje44bJFHpWv9S1vQeLG+gw9AFysLbA0eIbgftxi5TWX1CSUqXuCSQ131wq4X7v+fRTTpRUUge7QSiXXzFfVnb3q8ecdAvE4tfuOsxAW2dpaJZ+rQnIGfrUO50yHT1x1Eu0LHGCemZ6F2NiPGNAWkUfOiZ/5GD6x3ncgPfp06cPtj2jyZF71iZMRpYm2gdZ+YGVHSBDy494zqlf5EwaW/hFewekoc2TrhUDs3FvnBEyAjFDi8AJwCqBaYbHHnvMxbVCaFFgnP70pz+5MpmSAMrbisEBfK9atcrJIqpoBGTTKMgHkDe8cbS4p556ygVAXDSNxTUKZIhcrUEZDaa6rM7jRLQeo3VMnVP3rUK0Pl966SX3/qspYMW1Iol4EwP6ojLOZpJS6A9kv73fKrNnTnedW3d/SW665XZZ1aPejKp5JX71dnStTdPOra1Z5xs3oEP9Q+v3v/+9M1Cmi62ib/pmq8Qpj7WDVoA2/sILL7hzDBp0rb3HDaaOH3nkkcG+BJrRNgmoD5v6Jt4GzZQTA2uGmbwwtNQh8ffff/+g4b744otdHO+ely5dKjvvvLNssMEG8u53v9t574B8cQiQAQOBuNF47xkzVqxY4YyPjWKAKSUVRcX87W9/k0WLFg1eM/KhkpphHEYClX3BBRe4MplSENcq+gsWLJC///3vjhZlQHGMtsmpEZjXgAIbP9Zh3nPPPS5wbg2ANJzzTDMGSuRHnVp+nBMHzwsXLhxIFR+ghTxt9EwdI1fq3OLiBPRNvsgAPP744/L888+7cjUKslSnWDKSkmx6YIGTk3cgnfmk5NVeX/DBM6RWZr1BXq775a/kmsW31juOsL54zJ1qwLTXS0i5LNTjLETjRwN4piNE7rTzG264wcUjF5NH3KA/gT51Dqh36LcC0MFAX3vttYODUZNJM9rXaHDfffe5dg5dDFsz9G60+Mc//iFXX321o027Qx4me+LoD5ADbcIGMjaAIh5jav0y09DEU3/Mguyyyy5y0EEHuWe+853vOMNM2vPOO08efPBB57FDm1ky8iZf+leOIG45xK5hCGgoEwiVALgH44A4BPfrX/9avvKVr8hb3vIWmTNnjnzve99zgrV3CpYn5xytMhAyedh7ilZ0ntCm/KYwgLhoZxonrIFCy2SCLCyuUcAHcgXkT0CBoWHT2pwTZ/cBz5jBbgSmG/BlPNrReI8T0IIPa5CAslhjbRTkb3pKnvBk13QEAPrcs3pFv61zxpsEltYwWt2nhlJaZTrk0X9pqagJraoHnUjWJKPHThX/YXu8VTabvZFUwoysLGZkeVHrV5/LMLkd1Fe/Qp0usKdIefShSkGCUkH5Ux3VGO7rsFFqatBD7jMiGEXfhh7R7tEzdMzkhTxML+MENJC3zZKgd9R7K/oWAH2rewwNdY4+4Ck2o32NBqaXlAX+o31d3EDOyB7nDBlQ/9a/m2yQw9vf/naZOXOmHH744c5ePPfcc4Pt1J4D1F30+qtf/ao7MvD5+c9/Lh/+8IflmmuukWnTpsktt9wiW2yxxWAfB6KvFuKWQ+xSRnAwgTCskq0DJ457jFK+/e1vy5FHHukUcI899pDPf/7zbjqDCkAgPGcNhGcI5AfoHKhEEzgjoO7ubvdc3IA2IyzKSQCt7DzsPQv0kIl15ARTqEZgo05AHUADudJA4JPAuSktaQzRZ9cV8GD8mC5xDs+tmFqyDgA+7ZpAnQ81iOsC6+zJy3g0PSaeOBsMcQ9DxX06K+7jAfAs8iedyZ+0owGz2kxR65BODa52Who0Fkb1GEpGs0kom2ecerKLSuU75Z7fPCRLV/RLNpXV5/VJTVSq6sBMn8jl2qQWaLvUxEkWjSWcKXZeM4Efz6hj8GSNgE/qGWMEkD18w19U1+IC+kZ/gtxtIRC6QBlaAeoaWhxpZ8Y3xgPdiBvQRUc5Qhf61n83o38ZCeg1+k0dAM5x1NAD6sT6B8rFDOsdd9whn/jEJ2SzzTaTN73pTfLBD37QzapiDwDP8Qy8cHzDG94g55xzjsv/U5/6lFxxxRVuOpt8tt12W/fMWCGhQq/3BDEhWqGQQiC8O/nlL3/ppqjuvPNON3UdVTyOCBGh89y+++4r73rXu1x+NBbyIQ2NhOOyZcvctAvGnXtmxFsB6H/84x+Xb33rW668dCIbbrihUyJ4jVm8Mm/ePHnve98rG220kZMdvJuMkGGjIB/qAF7glc7S5M97MEAjgDb0bHSPLChHs8pAPpQDAwTtF1980c2wHHfccQOp4oHpIZ3E8uXLXaeILKzO4bURkLeNzGkDdMTwiP5wDt2nn35annnmGZeWToSR/etf/3rZZJNNXBrid9ttN5cfMgfEEZDVmmC/XREmtH2qpa4MPJ9RWSfDQBLKXpBqk77MTLnpV/fJqqIOAEq9ss+73ihbzOpUU15fmNRXUR1JZsT9+mSxT/Ip1Rs1y1W+o9Z8g4F32+SbCFUvCCpb6K4JpLEZM94F0s4PO+ywQeMYd/uCLrMTDMY++tGPyn/8x3+4a/SAeoqbPrKF3uLFi53TAl1kgs6gL3EPUNFvpoypAwwZ+kgc+klbN32LC88++6zceuutcuyxxzp5W/ugHOg375Gpm3/7t39z1xhu4hhImbdtA+u3vvWtrq/80Ic+JK973eucHaI9MXVufRi4+eab3TvnVgz+14R4JatAkQAdq3XszOG/+c1vdsq29957O6GghBwRJkfrkAGKAKKdPfnZNUeeoUJ4HpAf56SLM0Q7P86ZWkGRKQ9huGeaGVBIGioNxTos65ibQd/qgSN5WmcErzQCgskgmsaeGS7PtQnwYPwAeIRXeCZuuGeaGaweqVPqdmh9D/fM2gSTEx1FVHdnzZrl9Np0G565z0CW+7QhOiLuW5lMTnRe5Dsa/a8FlXoYeDZkprqWkGqQ1HjanF6HJQkqq+RdO71R0mqt27I5+f3Df5X+mg7WtFpKmk8mlZZkoPVd1rqXjAT6YBlvWjMMNf9ETQdvXPPzk6Hpxsj6CeAD/uks6Wg5cq8Z+jVSME+Nc4BcqRviKcvQ9M0O0OH7WlvMhDGhzonnfLhnmhkwgnik0KZ/Rea0Pfvmd7hnmhmoa2ROOagHo0+bADNmzHDnxFM+5ETZGNAQh06T/m1ve5uzNQxiMcykszaFt0wb4hw60IOu0RgzKAOxQhkMVcgDV2Gowgq18/in+D/84Q/hRRddFO666670/oNBFTD8/Oc/P5hWlcQFA+fqfYcnnXTSQEwYquAdHVXggZj4AB9asYPn2om781bhmGOOCXVk6eiaXA1R+TYC8hlaX+A73/mOC1G8Wtp1RTQf8oVHeIVneG8loGvypc6jsl5XRPnjHP5MhhZHML1Cr7XzCS+++OLBdmD3eBZE8xwJaiDDINR89FjTx8iR3Di66/4ePauEXaVquLwWhu885IPhFu85Jtx+79PDb116S8jd3oHntGhhlSIMkNfWENbCgl4Syq5c5BloOpdmIN1IgGfkoR6Nq3PaNXGtAnKm7Npxu3P1WAfuxA94hfaJJ54Y3nHHHYN808e1Cl//+tddMFAXzdD90YB2Tt8Ov9Acqtt2TXs0m8H5lltuGZ588snhj3/841AHvk5uFqL1h83BxmyyySbhFltsEaqBD9WIt4y/NSF2z5nRiApkcJTJqI84RicELYMbBTKaOffcc+Wuu+5ycRzPPPNMec1rXuNGNXjd5MMoyEZOxHFOvrxT4L7RhA75xw1o2dQi5WDkRdk4t/LECeggA+giJ/i2eGTeKMiH+rBzoEbAxeHtETgnDlga4uy8EZjeAPMS4dXqPW5YvVKn0OWcOOqcum8UpiMmP/hDb40OdLk2fpEBHgTx0CeOcvG81b1h1Po30A1oaxyc5ga8H8605aS7a5V0ZkXaNdmO279OsumMlGsZufSKa+RFXuVpupoWP6nP8rwWSYpV9cIlrUEj0B+3AIygl65ZUraRywef6IC1M/TK2tuo+WsAVi/UAf0U9YBXZW0gbsArMqB/o36pb4DX3EpQB8YvdUGZWgFoMX1vswTUg9kC6oAj8cwk2WIwpuH5muMXv/iFnHHGGYOzDZSfo9WfGm63Mps8vvCFL7hFyJz/7//+r/zqV78aKMHYIXbjDLMImE4H4RAQsCk719bZkpZ4FJFl7giP95qf/vSnnYBJr16Ce4b8mJZASXiWKQ1gDagZhmk0oJJRHngkQNc6WK7jBrSQG+VASTlG5doo4AeFNt4IyJf86TiswzSZE0jLM5w3Cnggf3iK8gjP8B434IW6hJbxRqDOKUejMB6QH3TUQxmcsqYT4f3qQw895PQcmUITeXC0a8A5z9s9QDlHRKLOn/7RC+349UCngAmgK66pvKdOm6KGV9uxRsyeMUW23HQTNb6B9FUScs0Nt7lV2o4S2ejDOpxz+erwQaO0LXAkiiT8cYAWFOrG5tWAfJAD0/lmmOCxVe2LeiGY/AEDUuLQwbhhtKyvQx4YJ9AK+sicgD4ic9oA5bABYdxA5tADlIN2Z9PR3EMexPNpIQu/eJ+sXrMrK3KyNoGsSEc/QhzfOH/yk590fNDmWDimHrpbu0O6b3zjG+65sUTq33iTHiNMoTnaOcwjIASLABCYjRCJN0U02HOkAdYoEbhVEgsl8L5JQ35mmOzZuEB5WZjDYgP4sQZE2eKmDaC/0047Of6RKw3ZFBbZNloG44W8TP6WL9fMbGy66aaOnsUNTd8IonlR19ChTOgIRuyNb3zjQMr4YHVJ3SJfOiV45vMN5N8I4M1mgBjls+Dof/7nf9yiL0bzfN7xta99TY4++mj3Lo10LKZk8aN95kG5rE1YeSgv7QBZjQwdLId1w1d/Hh+avzo4K2nZ1FMOK2WpVUPpmLqBGuO0/PGxJ9SzTstfHn1UjjnsIGnPaLsMdfCkdxP87qTSJ4+0M9B6HZKb6qLmjwFPOMNMQD+59+qAD+oaHeAdI3UOfya3OEH9WL1vvvnm7vNO+hbkZDofJ+AZ+hx5bwptAjppdR4n4BMdQtdYAW39LeDYqP6PBKO91VZbOXrwjjysThgscDRZIBcCzxFvfRVH4jj/7W9/69oTCzzPPvts92UQ96hP+tElS5bIE0884RaJsQhurBCvZg0gWoGcI8honDUwBMc9U0YTuCkEAkaAeM+AdFzTaTFaIh1p7GX+aBSH5wnA8gXEUckABTAvkPyBjSAp1zbbbON4ID3lXhuMRN/oRulzz0atW2+9teOX+/Bv5ULZTH5rgvEIeM74syOAR4LxS6AMLIyx1aPkE60v4qJ5vBp4zvgmPTSMN+6RD/SMb/LmPjzDOx23pbXnSIccOI4EKyNpo+eUA5APsiRvjtChrl/72tcO8g1Ib+eWjx3XBPJgVuh3v/udXHLJJW40f/rppw/Sv/HGGx1dOhBrJ3zqwXMG7nNtcVYPNkBdExCRFVPNjV6ocQ3L9XM1nvl8u1Qr2pZS9W1ap3W0yRGHvE822XSOK2NvbyBz593qFo+pJZZypUczqklBjTlRTiQ17WZCLVOo5dP/bqrbhZFBXVibos4ZCAPTgaiuANJH6280oJ4I0TokD0C8yR3jjIzt3trQWFdAD/rs90B9cs6gJNpXNALj28BCKdNbjsgDo0xbHyrrZvBvtMhzaL7wyWBs9uzZ7h56jeyjdWK6YfpPfLQPHtom6Ev48ofvoMnrv//7vwfTc++0005z3jnt/ogjjnDxY4WWGOc1wYwKAkc4KB2djRkZUwgqijQI0iqG50zo3EPYVAbCJQ/ruNcEaJIeWuQLPWgRT94oBXlBlzSUy0B8VEG5RznsGVO2NWEk+tAlX/Kj4QDSkBZ+SWf34Rf+rdwmuzWB56Ft8ud5zokjD/LkSDz3jQYgjc1yUE7u2bOW50igrHSy8MIzXEPH7nFuZQRR+VtZuEca0ptM4N3yWRMsX/LhGXjlOeRJXvDFj1wgbyuPlcHkAIgfDb2hgAbgEyFo89kgIG8CHfL222/v3oNBl/ISxz3K0yhgASdWa79+LVrXLtTlosMhSaW1fiqq16WyTGnLSqF7uZxz5qnuG+hkMi1Xz79Wuvt1oKzpk1kdyAQlyWey+gz5KVADwuBFnefRAl7pF6gLdIX2Qn0QzxE9M12zeuDeaGFprc1Cy+qZI3pGHOkI0KLeRjP4aRTW5u27euqfNkcZuG4U8APP5MuR6WvrN0yuyAA5c7T2ZW2iGTAa6DPl4Ijs4dP6FOrdymp1Ptkx5sbZKsQClUDFIHwaCw2AhhFVSJ5BSayhmOJYXtZoeGYkoIi8r4YWIC+eJ39TWvImXVQhrLw8R6dBWuiRFnA9GoxEnwBd8kU2GG7um9KSzhoMefA8ckEWlueaQFo6O5Ml+VIm8iEPKwu8UhbiTSbwa/QJpOVZk4nJYk2ANs9S59GyG00wtI45RycYzUMHWPmhz3N0MshqJJCf1ZXlRYdoAyToRD/XIC20uMe1lZE4A/FrA9LzzTZ5vOc97xmIrYN7xLG3MXs7Q9d0cW3pDAc3u8xxoPwc8Zox+xyJLathTqazklL5VEr9MrUjLXvt+hrZYpPZbjqcT6Z+dvkVUgypu3bp6dPBZlBTA13PX6PrPc3AO+b6hDeRq2X2akAP4NP0jnqxxVDoDIF4dI60VpemQyOB+jV5coR/9BiQB+2Ba9oe+sF96sD0IG6gx3wWRDk5B/BMn2HlbAS0P/JBhtAA1g6QCXKFV+7Dt+k9bYJyNAqTOTB9NhlTHutLuEegHIDnqJvJjDE3zjQ6Kt86X8C1KQwVQuXQYaIMppDco/Gwsxjfn/JxOZV64oknukqlYZqyrQnQJV8qmudNASgL+UPPykfg+rLLLnONg0Dcv/zLvwyO7HjupptuGizfSBiJvnUOtlqTjok0xMEf95nm5Bs+FJnFDZSXBk1+I4F87btA6JIv8iYPykXg2uqGMs2fP1/22WcfN83H1DKdxuc+9zmXFn6srmhAIwF+SIv8SA9d45/ywyP8AuLZoJ537Lx3ZAcf3kXynpb6tvoiP57jfCRAh/yhC8gDfmwwaDK08iBjNn7h/TBxyN8MiMHORyN/8uB5Nlugw0MOBvKBF/QbXngPRnrirNwNQ4s4sD8IBVaiegi1E9Yj0VCo8SeVlCef+Luc/cEPyBu32VJuXnyXvP/Yw6VU7JZKrSw33nKHrOitSr+KccaUmdp71uqrtzUTJ4YBUayWCblbeHWQngVx+++/v5vaZaEocbwrRGfRN2QBTB5rIxfkTZ2Sh7VzgA6bPrH5CPdp59BmdoOtHamHuEH7pJ/BiF511VWuLZ588snuHnGNAj1nwGODD9og7eyd73yno8t9Xhmyngc5EWh/wOTeCKAJH8ieQP6UgbxZe8H7ZuhxzYZDyByZUC9WV5MVjUu3QdAxWYXQGKggKsw6aOKpEJSEwLml4YPyb37zm3L55Ze7pe+8t8O7wNOgEUU7ulcDiklepIcWR6NP2QBxNHjuA8uXd4Qo1t133z1oRHjmgAMOcMpDxz0SRqLPOcCAmgID5IARQXY/+MEPHP/Ii7IhR47kMRIwbuRpAw3KzMpYQFnIn8ZAWbj+r//6L7eqkXN2rcJgXHrppXLRRRe5TWWIh3fKbfJaE5Af5aWs1tFCExgfdMKAgQedMgux2NWH7V0/+9nPyoUXXug+wzPwjNXRSLA6NpqUGRkgE+oTXmzgQtof/vCH8pGPfMQNiIClg2+wNobBwLPIAVrQIA9rC5SLuiYenuwecjKajYApbJtmDt17YYJ2CxqFo1ssVSWbS8r9D/xW9th7D1m5cqnk2Qas1COHHbCDvHbbTaVaK8ny7pJcuWiJVpoOjoK0tGn9B9S/FjFUKx24AB0C3Y6FNeP2228fNAb/93//5wI/RsAAkXYGTH+QCefICNlxPRKQLW2Q562t8TxtCwP9jne8w7XzuXPnunZueR911FHys5/9zKWPEzZLwC6IZ511lqNPWdEX+sNGgQ6hV8gh2v7If7vttnMy4LOkP//5z45v2gaDJWRmbaYRkB91Rl4ErikHztaXv/xl9zkUP7zxwAMPuP59zz33dH0h7YHyTGaMrL0xA2VA4agQBI6ymIJwTYNBeayjJy3x119/vdx7771u6TwjWSqYTvv973+/W1bPC38UbjSwPM0oYmitAySeI/GUkSPKSvkwaKSzPAAKYx0E6UeDNdGHjvHOOfHQ4BniMaQoMTJAdhgS+Cbt2nTeNDbokb/xZXVBYyA/wAIKPGa21KOcpDn++ONdx0F9MGvAszRu61jWBNLAO/nDe7TMXNM5QJ/O6T//8z9dZ/mjH/3INWLuf+Yzn3EraPl1Lniw58BoBgfQHionjCQ8IGPyMnkwS8MnFr/5zW9cmegcTUYcowGYTqwJ1CXPU/fRgYrd4xo9ghfq1fK2NI0BQ4mMrJPTvAPVZxe0awgYaKXlNw/+QXbfey/53n9/V4486jD1lvtlSjYlWU1+2slHSyarupjIyLwFS2RlN16nDjACpkTJsSxhglXcvJPm39pNx3/xi190MwcYY15jsD0u37OyHzKrbtn+FzmZfgLT49HQQbboIM8QyAvZEhgEYBTYcxkdR+eoB1bLA8oUNygTfHz/+9933iyDQq4pc3N0oK5L6F+0vbz88stOv5EH9zinrSBX0IyBASBv029occ6OXQwAzj//fNevUT4GaNQ5zgDfMVt9TWaMOXdmSFA4AgJn8xE6Iev8OGKgOacDowKZyiSOVaxUKorD83hRdOTsb03FjwTyxjMkLzp3Pko3LzJaBjpj9nOmrHTeKBP3KC88oLTEkZZycByN8oxEnwAf5MXUp3VElIE03/3udx2veI7IgDhCtCGtCZSVdOTLkWfxpqFrZaA+6JgoAz+xRhkB94gHlIHn//rXv7p4+CHPkYCBt1G40bO6hu9//dd/delYgPKBD3zAdZTIGRlxpPysvuSzCBougHcwmvqH7sc+9jHHGzRZfW7nlAdjYLIBeBBMp5O3DQaGgmcBZRst8FIYWPFbzfY8R/JgAEZ9I2NA3GhkOzJwj+ng+b0oLSvFdV4zxll1T0NZydz7m3vlzrvvlH3220vvV6Qjp+WrFZ1N32vPnWTGzA5JZdukp5CU+VffLlM7NY8K5dPOPsGqbTXQmni1NNTgKOmBr7fWCAZjTCuzIIp6Re7UGSuIqSe+VzU5cz9qsEYjf9Nf0tpg02ggcwZ/xxxzjMvXdMLuMXMTN+CRfR7w2vmkzurd2nqjQIfJxxwZ9Bw9RB7Wx0CLdNauaHf0w3bdCJArPFpeyNhmJBiY0f6oe4AjRlug/fGctcnJijE3zjSEqGIANh9BOYjniPfEkQrkvRwNis1J+AaNiiUd96xTQ4ExeijRSEDJ6JChwWgUrwxFHEqb/WVZ0s85Rppy2yjWFAtFpgyUiTJybySMRJ/APWhsvPHGTkbEoZwMUPgmD4+ST0yIh3fKMNrOm7Q8B23Kwjm8crRAfdBQuc9ggBEs5YNfnqNT48cZoMknRoDnRtN4kCONz2gTyI8jPPOOmc6CBskPTTCVCV0aLflDk9/5pXzUOc+RJ7B6WRNIz6sR0nLOIMDqDhmjb0aHH7ugYwbGG8/Zs4S1heXNimzygRfi0F2794c//MENDnnnybXpmel746h3A6uLr/kmtMPUA1z+qw78eMfPL06lMzkpljRhUHPfNrepOD54xilSLBekGqZl7oLFsnSV3k46t1kNMovKMP1MoK+9fNA3BmTIhnYFkDODMY4MJKkT2gjy4BzZ0YYs/ZrAQBB9Q9bkxzPUO3I+4YQT3K5RfMtPPHGAVyroJL8PEDduu+02184ZoPDdLfyh35QVmTQK+Ccv8iVwDv+0A/tsDcC/6Rv3afc2sGkEVl/IP6rv9O2UBTrIGpq0b0B8s/gfzxhz4wxQtmhnY41q6LUZLDxNOmcWCzCa5P2Eve9kR6U//vGPrrOnExsJVD6wlZCA54wmykPDp4zWQKFDWXgPxY4yTL1wjyNxpjxW/jVhJPoorqUhP645osB8E8v7TxbJQI9nUHBgSj8SyIvAsxg4YI0AkC+NkLzMW+WIPIinY+M9LO+9+am2Aw880D1HnqNpPManGdShIA9kYwYbWVAGOhXAT7vRgeHRsziN9KPh20A5o7TNWwBWNpMtHQRytTiejXYqxAGjb535aMBULc/zWsDqhHzRPT6z4l2bxQOOa5P/8IA/5Ki6rcYzierAHuLI6HVajZ0a1LBakymZdjXUGTXCeq2PYW5Jnq2V5KA9d9G2uJEUw5L0apVfds2vJCSPGhuQpCRgcZjmpGZF+kvqcScw2Xp7wFbDd1RXuDZZAnhF/sYvbZ9BG/sL2IyRDcwAR65HazzQJeqMeudZ6tjaEbS5Z+2DwRM00TXKANBNYPStnKPRf0sbLTv5oWuAgfAOO+zgfpXJwD3KxwCkGSA/+KO8nFMGyvXUU0/Jfvvt5zYAYWYH/tkYB9qkebU2uzZAvsibQJ/KoAtjDE1eITGV/+53v9vVzaGHHureO/MM143r/ziHCnlcQxuY29hfFcddawW6a1WmcM6cOW6T8r///e/hb3/72/CRRx4J3/KWt4SzZs0Kn3322aZsjq/K6vKhHNpIXZx2pKEqiNuMftmyZe6HNyiDGmcXzwb9gGeaAfLRwcbAVR2qtKEqcHjXXXeFL7zwQvjnP/+Z1u1+iIL0Jq9mgLwI8I/8kYcaDFcH0IRn7bAGUtd/iKFZvEf54BzaHNW7D2+44YZQPfVQO0p3HU1rddYoTIcsb3hDBvvss0+onVT43HPPuXhAvA4c3Tl6MxqwKT8g/dlnnx1qhxd+//vfd3FPP/200+/p06eHjz/++GAZDjnkkEEdaxWM9pe+9CVX5wsXLtSrWlipFcOCnv3wl/eFm+11arjVPv8avvmAD4fPrQrDSpVn+lWGPWGh1B8Wg6qGclgOK+4HMOyHL8g7WndRoHNWj9Tx/fffH+pAJdTOOVyyZImLJw31ZHVFPeigxp2PBOjyvNGHFnVh9acG0B2PPvroQV2fMWOGqw/SQMue5ZpzO1r8mkA5rdymC0bzlFNOcTTpXx566KFQByXuR0/USLn7zQL8R+X1m9/8xvGpzk/405/+NHzmmWecLlrdo5PNBv0bcqN9QXvmzJmuP33yySfDBx98MNRBUbjjjjuG6gy5uKH94WTEuDfOpuA0AjM6GF6UZOONNw5XrlzplPZPf/qTq9wFCxa4e2eddZZ7rlFYQwEoDjSsHJSJ67vvvttd03nQeFAia3CNwjp78rOG/NnPftbxSAeJ4pLmj3/8o4v7yle+4tKPtnMaCfCIfAG8Ro90UDq6Dq+++upQR/fh2972NvfrYsDSNArrnMkv2iAXLVrkOkkGY0888YSLo6ykt/NmgPzQAejTeVq9HnXUUU7eyIY46t/u8QxlNaMyGpA/4d///d/DTTfd1OWtHl2onosb+AHyRQePO+64V/xCUdywNkD5vvjFL7oBxLx589Q081tTlXCllut5vf/u4/413Pxfzgi33v2M8Ns/vcn9ulU1QAYqi4oGjLleFSoDuqEWGrkRohgaZx33o48+Gu6xxx6u477yyitdmqFy5trkMhr5WxryR7ZGN/qsnd9+++0ub/oW6ue73/3u4D2eNd3juDb6Z0YZ2uQDLrvsMkeDtg7NBx54wDkCs2fPdgMFaDSjjcO3gXqm3MYTNIj761//6gwi+OhHP+oG5XPnzm2K/kEjKmv1nB3f1DH80b8zMOGcNs+98847z5WzWX3ceEV93m4cQxXWTU8xjcF0io6q3L7GTCfzDpj3tapgbhqb+3vttZdLy/STKs9ALusOeydDGaANDaZzOIcOsPu8/+J7QKacmXpvBshTFdjRgy7TuLyDYotHtpeDR2SkjcjdJz3yoJzNAHR530menFscPBOgzT61TG3rQMG9M6e80G+G/G3Ki/w4Ah3BO96ZQmfzDt4J8gMBTM2RxuqK8jWKKH2m88lTOwZHDxroHXSJg2/kgayYVqU+RgJpCeQBDRb/oLvQIe/rrrvOvb4BlIOpRdIjW56JG9ChDSBTykeAV3sNw3Q1YHL8zFOOl0yyvpHQVdctlhdWiZRqSffWOZWutxU0IuHmzwMJa1pP3B3QK2B6ZYEpbGTJt+W8vtEO2cmEb16Rj8mZ8iEXaJve8fxI4FmrM+RLWZhWpW0TB6+k4Zz8uI+us7c5r5RYOQyiPFAvXI+GPvmjV5QZ/QG87+UnD/gkFF0nPyufGm/3jOlCo6Cc5AmQHdemt9AlzuSC7HfddVenA7YhTqOAb+hZnbH+hMV+tGnoUDfQp555dQlYdEr9NIP/8Yxxb5yjygJokADFYGEGoAKpPCoYI8W1dSaNgrxoDCgD5UBBaXR8VgM4R7mhRZlIz4DBDHezAG8oKY2CRswPIiAbVrMySGHFMg34wx/+sFNaNkkYTecwEqBJZwGQN4ui6Bzh0xoVdFgcA/+2epayUAeNgvyhRZ7I9IILLnCrOFlBTudoHQT1Tx1Q//CPbAjNgNUregBf0IF3ZEMA3IcuRzNm1uGsCTxv/BGgBS/QovzkSRryI53lb+njhnWQBPQOniiXDUS0diSv5WOVwiH7vkvmbNAphWKPLF3VL9csvlNqlD3gHTN6wmdKyFMTB5oPpjpSR8aT1R2BgeG1117rNt6gw/7Od74jO++8s6OPbDDelIlz4ngGWNxoYDoDr2b4AIvReMcKiKNs1D+B991c/+Uvf3Ht3/oo6ok6JP1o6p88TK7kQTn4IoDPNfm+F8MNTywGxClh0M/nY8SxkrxRUFb0CcAH5UYGrERXb3mQH+IoG/cpL85RM2B1BA0bYBPHJ2wckQvlMn0gIDPKxflkxrg3znQAVAINiMbDgiAqjE9sUNSFCxe6dOY5s2CA+wcffPCoGsdIQFlsFE1ZUBg8Gb475JMtlJV40tBRsEkChhLPAiVqFPBA3jQO8mPVJkcUliPGmq0dH330UXfNRh2kZQahGcoLfToI+ASsDP/qV7862GlDEzqUg2tG+3QyNB5byNYIyNtos2MQcmfRn/2kG2Wj7kljAzNgnWijIE90gHJQDxytE6eTwpCShmO0w6A8pBsNSAsNyk6e8IUM0W/owAd6Z7KGnpUlbkCLMtGBG03KQRzn/KuWi1Iq9Lnfez73zPdLWtkOk1n5xVWLZGm3tsFkmyhXkkzwbapmqlVUq5brS8G5iMBkbbxhIPjGmD0M+K7YZoYoC3JjIEwZAXF2b7RAv81AIGvowyvxjz32mFvJj9cO4BuaBGaJAF8nWD3zLPVm7YLrkQBtykxanqFd2wJPyoBuc86gl08FMdDve9/7XDxlaxTQADgdNsBgZoBf2eMrDeIoE+WDbzY7Qr44BfZsIyBvdAlQt9QBeyZA49JLL3XygS4yuPnmm1058KCJH418JzSU6XEP7fRe8T7Hjrzb3XLLLcOHH344VOPg3gltvvnm4etf/3r3HkeV3qVtBNoI3JG8LL+f/OQnWF33/ot3JLfddpt7L8hCFd6D8g4aaKfhjo3CeLb8OGoH4N678M6Zd1Es0FKFDdWjd++CuN8M/qFNXhzJ7xOf+ITjnfde6jU4vllAYos1WJhGWuqM8jUDvMtfsWKFWxjFu20Az/BuQCZWVkP0fF2BLMFQflgQph2Ie9+vHcwraFl9jeadmD0HHWgA8hyaX5Q2sv/1r3/dNPmuDWxRkBpK9865WFW90LOunhVhn5aTFRLvPfbD4Wv2OFvDWeE3594UrtC4Xk0FdyUVJ8WuljRllbUMdVnBb5RnzuGP+uYdPO88eb/PgjC7j7wI1D0yi8LqbTQgLbptz1CfgHetLDZUj92947733nvdvY9//ONOBh/60IdcOsoS1T3OR9v2ouXmeQuUhWB5QvvFF18M1YANLgizvqlZgJaVG7mrUQwvvvhiJ3tof/nLX3Z8H3PMMYNlbAasvUDb8lXjH2677baub6HOWVNEX7/ZZpsN1o/JZrJiwhhnQGONdnwo9plnnulWzaI0GKdzzjknXLp0qUvbrMqDJgGlsfPrr7/eLdaBLkFHcaF6dIMLJ+gwmqG81liiBsA6Ze6xWALDxQCFcqjnPJiuGfybvM34gYsuusgt/tJRtVtZCV0WKdGIrGzNlD2gc8QYQgua6t0Mnpv81ZNwMicgm2bI3/J4/vnnHX2jZ8F0j3sMkCw9/I9GBsbfcOW2urdrjuRJ58iCsFYAmjvttNPgynwGnxyRg4tTR/rfvvQFtzSsr1QMu5Tlny++J9xqtw+EW+99bvjGA08PH9cxJQa6n1SqHjWnIiymxDDV+Ycv449Am2eAjXyNNufoHOcYDq5ZmGdyRpZ2DkxuawLpTc6APKLPMQikTzHdg/4222wTfutb33LPoe+0DcD5cPW3JlgaKzvPRtsQ5xx/97vfucEJC6Voa2agmgGTmfWzdv3JT35ykGeOfBlhbaxZsLyMH2sP9GlnnHHGYPtC3xgM0beDZpZhvCLBH2V+QoN3okx/qffmrrUi3TQIx1aAd0C2WMHoqoK3ZNqF6TW+CbQNUUBc/FuedkTmgHeBQ+81E9G8AefsFMQ7cH6APm5YXUZ5szrXTsLds/hovVt6S6MdkJv+1g7IxTNdx7l2/C5tNH+OpLf3gZYvRxZD8a3t7rvv7u7FCSuT0eddKNd858uUdC2oSErj1cZIMp2RUpiQ/kDk0OM+Lku7S1Kq9soHTj1aznn/gTKVJ/RmWz4p5VqfpDMpSbqPqtfcTqwMtHOmdtnKMSqruGG0+J6eH5iJxrUKvDbiPTcLplpNm3YOPfqZViNa51G0WgZjgUk+ae/hES90ZO86CvWA3PsyOgyMqnoh7hyjRhqMMO/JWPTCNYYZYJh5DmD8MOTkxztAM8zjGXQggZYZnmpqoOGqIyVy+snHSqF3hSSSWZk3/3rp7nObeSrfOsipskajTQ20DkjIZB2AjDw8JjO8cfbwaABmmDG2LJ4BHDHEGGaMMsFG+ix6McOCISaQzgw0R4w0Cwox8OMd/CQk/CcSA4vfAj3Xw6EHvUO22WpTF1WtJuUXl13ldgRLq4i6+rulpDynU6zx9l2Qh8dw8C3Dw6MBYGjNCwZcm8EuFOqf6OAdY4SjHjLf0nI0L5p0GGMMO88B4sY7dMghwYD/m04lJRHqVbUmee1ZTjruCCkX+qVWCeSXv7xDVvWG0lupyZTpU6VScx9SeXh4vAq8cfbwaAB4wxhZDCseMucEjDHeL5+8cI/Pysxw8wxT1hxXrVrljDOGmyOB58F495wxydVaIMnUwM99DgxU0lr8Uqki7zvg3fL6rbeQsFKW7q6iXL3wegkzKSmoOc/oUW24h4fHq8AbZw+PBmBesnnINoXNOd4xRtkMNwaZKWwChhmDzAIfvt/l16/IA2MdzXN8IylMYifTWs4glAqDCbXYSf2TTiekPS1y2onHqxedlEA95avUOK/o65fuUsF5zXwP7eHhMTy8cfbwaABRr5mFYLbAi3g2SCGOXa4MTGPbkcCvefE71fw8n71/xoib9zyewfYhYTKlx6SkEqGEtaoz0iCTSkihVJV9dn+TzJ4xXbLZvPT1l+TKRddKW26KVDWZt80eHq8Ob5w9PBoA74eZvsYoY1jxetm9Ds+YOD6d4px3yUz58pN4eMWAXc7Y5YnfJmenK9KYgSaf8Q46Dy2qQ0IHE9ks794Tel4/duTS0qGnZ33gRCmrt1xRc3z5ghtlWbHqDDPBPoaBW7zpOtdkaoG4hIsPX/HljO+6PCY3JryG04kR7D0fsGnDVoEO2jpTPKhWA34BPBOQg8miGSB/8jOZRo/DxZmBaRaMnyi9ZuY/WljdUte2aAvja2AKm/Lx4x+kIT3l5BzvGqPM9+gYYe5hrNludsstt3T8EWfGnGtgfJpBN9nidZOv6Z3JCETjG4XlQ/uK5mnlyafSkqKI3FKjjBftVmXrkQ/Bcnpx+AE7ysabbSilICmrSu1y6bxfSlqrMSyrDGtlKRdLwlI5cuwrIlfNsFoUtejKk/KiaXn73l9W+Sfr21omNS6oFyF2mM7BP3xDnziTQdxgJgZ66EeracMz+gY900WLawWgBb/QM/3jnDi7nqyYFJuQsKc1myPYj+0DU2CbRowLiI+P9OlgoU3HS1yrlAfa/PCFLTiCXzpSU2CTx7rCeDF+yI/A1OuLL77o0rAJPtO30CVYWnu2EZhRMJ6sc2Kh1csvv+w2QIkbxg9Hm7Lmh+ihPRJ/lJd3x3SsxgeGnU+qkBnGmG+f2ViEX9jiF6mQp3XIPPPss8+6d9HkxTU/yLD//vvL61//epc3GzXsueeejobJn7TIqNH31uRldc5MAPu4o2PoXLWqupVQfQt1sIB5DZNSSWYlUCOd0jjWY+fVCleSebns5t/If/zocqmm8jIjn5B53/6MbDu7XWraRktBQvrChGTSOTX0ZUmHZcnxvNIuJdukT41yRvWtr69Xupa+KJtvupl2XGnRJJJI08biMxTIGzCQYv/67bbbblC+xNn9uIDc6VP49Sv0wl55oB/UR9z0Ab8hAM8zZ850OgZdrulfKUucoG0sXbrU7a0OTBfRQTtOVkwK48xU4cMPPyyzZs0aNBI0nFYoD8BIQRtR0hmiNKAVokVxN9xwQ9eArUO3zgM0qrzwYDK0hkFgKjdqnNk0g3QWAOkoSyOI8kFZCMYr9Y7c44bxAF94wFwjd/geDaw+6NgwyuRBYCobAwouvPBCuf322+Xuu+92nR+yg2f0mB8bIMA3uPXWW+VNb3qTzJkzx8mBgRm/0MVz6D+0MPo8b/JbV8AzeRAwDAyIKBMzANBKp7Pu86mUVNzr5loyJ7VEcsA4q66o95tqny4rpFM+cuE3ZFW/5lXskeP3eoccc/DukknoADqTll617alkRvLqEleKvdKWUg+Zie6MDl4KOojpqP/ASc+KVTJHBwYJHQg4/XLqHZ9xpu7oR2jXDIT5OUOTiel5nDCdYZcsBkTUMYC+tYk4Af8M/uCVRYvoLWXg2gaDcYL8GZjyU5WAOifOeLe2ORkx4Y0zSsro6umnn3aehFUcldYM4zASyB+Ph1+SgbY1mlY1Hn4Fiw6DVb/wG1VYytMs+pYPeVoDQeaAX+myOI6gWXK3egTGG3RosHiU22+/vbsXF6A3tE4pzz333CPvfe97RyVfnsOgmWHHyJIH8XR0xNP58DN5bEuK0YZHOj+jawYbY8wCMt5rs6Uh+eKJY4xtpshkz3Pk0wjICx4J5IXMOa4emNSNsKZyM9tBQsspOkBzfzVGn+uvqsHNpmT+kt/Ll//jIpna3iYdQZ8sXnSJtGVrktX8dEjpPGHeVnNMpqoSVHWwqYa7plY/oUZ/+YqVsuLlpfLa7V6rZVD+1HNPMj8eI+AfuSLne++91/3iHHHIgHqzAVNcgDZ1j9fOL1KxyBDa1hZGo3+NABq0c+jQzo0musg5IU689NJL8txzz71im16jafUyWRH/0C9moCh0QoCGYpVFXFSB4goABRraCdq9oembHfhchw4bUAaC3QN23kgw2Dk0kC2dE4Fz439o+kZDNB/jD8AzvEfTxhGAHQ2UgToHQ9MPDQD5oKd4X6av5EGni2El3mZ8zAgDdNk6Z+TMfXScgQkzFdxHDhhmno8aZvKw60YC4Ahtyv7KOldZJDASLhEXeuC1Qz2ECW1/mojnMWGH7beTbLvpbCn29sizS3vkkqtukiCZkrLmi0HmJw54j6xRml9awhSD3Yr7blqCkvbGFenu6tULhaaFfrSscQR4tj6FgZPJAQyXvtnBdABd50hcFEPTNzsA6hv9MsA/AVkM90wzA7MGyAB6Fmf0OZ/MqPd0ExhWcXRSKBEKbNMt1qjiBLRRIAB9OkSjz724wVRjdPRuCosczGg3Ajph8oQfAE82GIJXAiDO+LVGa0amEcADvIBoY4RneI8b8AQ/5sVSx4A6H0398hxltbrgnOeIN4+Xa9NVm+Y2vs0wA6bxTa+RreXNMWr4Odr9RmE82pE6sHpwcZxrCAnq/daBfpBejbla25R6t4XesmRUHU47/giplYsyfdbGcunVN8hL3drRJrSt6CMs8iIL1Kaohrj+mdYA/Vogbbm81kFdTlW9bzuGxgnTPeSJjI134qPtLi5Az9oT9c4R2lYfcQO+oWu8Gl3rD+IGbYSBQZRnO7e+Z7Jiwhtn80JQHhoPikSHRuWZEYkbdLDAGi5H6JsyxQkaD3xyJADoI4Nmdx5RnpB5NIA4eIYHeDHZGp/Gc9wwnqJ1C6zOR4LpIHqJscToIi+uycOMNHHQieowAR6JI/DqgrQMSog3PSdPK5eV1fJoNqy+jV4dnNe/dwbWqVA7Fe1IU5p2WmdGOtWuHrTvO2WLTWfKiu4+6a+l5JrFt7lV2i47DXjcNY3BYOsQV1JJ1eFQ+dGbaaWbzdSNcyKJXKEQrw6YbgPqwGB6ETegYTKPAvm3kr4ZQqP5yvqPD+iwOSBG046t4H8s8coan4CgolAcjnSEVBjn/9yBxANo4O1AFwWi06Q8lGVog4oDUX4B9IlrlvEyGVpDiDZU8jcaxFkZLG0z5E/+Vq9Gy+rW6MQJaEEf/qBPHUOXOh8NfxhgPF+MsBlc8sSgEjCiLOgC5MtCO+PZPATjnzLYoIB3j9ynDPYMMLnYM82C8Qqd1bRUD0Kt8zCtBpW6/2dPBn4DNbYsGKuV+6RNs7ngQ2dJri0rpWool115jfTx9RSPB2XNlFknNfPKq7ZspcEAA4OcklKhqDypUU5oG2N7MebCYwYyR86A+jK5whfXccNkDV10iKPpP+dxA1rQtdkbroGVK27AI4E6oBzQpc1Qjmbq93hEXdITGFQSFUbFmeIAKi56HScYUVvnxZHQKtpGFxhto9+MMlj+li+wRjFSnB0bgfFh+UbzbEb+o0GUPuAY9aLWBNNNRv+mkxwx8pYv13T2gM8CiecZOiECBsLka52iGXYDzxBIS552bBaga2XlnPzrNwZs5GA/qTwNnKmk9L+WS8/CSlFymYTkU1XZ81/eKrNnTZOkesE9vYHMnXeLlMkjFUqx0qPP1KTAN86aZxhoHlVyTEkab7rCojq8VjWYaqRbAXhFtnaO3JHDaHWgEZicrW4JVq/R+o8Lpkvop9G1srQCpnPwagNbQJydT1ZMbu48PMYYjPjxcjG2nGPY6FhY1IWBtk7n/vvvdx0Rn0dxxJt+8MEHB3IZx8BzNjgDzTWdeL0jB4F6u25Vda2oaapucdgppxwvff3daruzctX8a6WnX+Wjz7A6uxxWpC2bk4DvqF2e+qx2xNhpZ5DNKEdpe3hMMnjt9vCIERhfVlZjgDHMjPYJTEVjrG21PfcIxGG8CTvssMNALhMIoVpQNZrYUToXJqfhSUccGq9etxpo5U4O2W9Hee1Wm+rdQMo1kZ9dPk/KmjqVapfu3n6p1MqSz6iseIzMQJJXOBo4xzAPeHIeHpMR3jh7eMQIm5LjyDQoHjTnNiXHdDfGG8PMqlTeZWPMWvE+sxlwn0upjbSOpG4u9cp5tUk1w7Y2QO+k6+/rg0pROjTm/ccdIaVCt5SqFbnhlttlWW9F+quhzJgyU71s85oHoI/jOZuhTiTIf+DCw2MSwtqUh4dHDODdHIaYqWp2WrJ3d/bODkNsu4ZhqJnOxpjbwp/xjoR6s2ZFrbTq3CoGjLPa2Ay7hrF2SQ12KpOXrMqgWg7l0H3fJttuu4lUg5Ks6CnJvIU3S5jOSyVMSz6bV+FUXGZhMpBA6bhpbQdO6vmvpurhMbngNdvDI0bgDWNo8YzZ/hBjjKeMgSaOI94kRpm0dS+z7lGPf/Dul3fAvC3WwYTazMRA+UFC3VymtTPpjBrptJTcqq+0W3vdpn86dXxy2slHSzoTSlmycsXCJbKqS1Q+mkCNuftqSvMONbDie7VxxujrhX/n7DGJ4bXbwyNGYGQJ9ikKxhlDjGG2988YaKaxSce0t8GeGddI1D9tSrhFWlXtUVYbZwdst0YlUzn1r1l1nnR7cLepJa+WKrLPXjvJBhtOkXS2XXr6EnLV/Nuls1PtLku19WHMdi1R1qN6zmqxnVF2Vlq7riGkPDwmE7xx9vCIERhjvGEMrxlgjHHUMHPfprCZ0uYZ4lvxqU7jWPMnNdVq/Vtc2Mtm+ZxMeVdvOgwq0pnLSKfa2XPOOEUK5YJUEkmZu3CxLF2hD2g6gEeOG41xjnrK2GVvmz0mM7xx9hhnGJgq/adgqHfaddUd/+qLscXQEvh0ajhwj3QAI23n4xHGSx3IH+PMN9ocB+rE7bFNEMnlNX4g+eoBSUrSyYz7pCpXDuSovd4lc2Z3SqI9lJX9Rbnimv8Vva02mUlxNcu1iuaelKxG1iqqC5pxsRpICXvtcvbwmHwY/72bh8dw8O8bWwJ7B/7qGDDIg2EtoFnn1NDygxenn3aClIo9kmnLy3WLb5KX1HuuhgxS0pJOpaRSLkutymYtbRKofXaDmDU77R4eExq+h/Pw8Bgb4FGnE1IqBXL0vjvLnKntbovP7r4eufKam6SmtrkasqgsI8lU3f1OZbNu57B0kjfYg065h8ekgzfOHh4ea4WRvenRo1ytSTan3ZB6wx895wxJ1opSLBfk6utulJX9el8tdKjdVDaVUUscSAXLrMn5qUq3F7eHxySFN84eHh5jAkx8KpOqv60uVuSIvd4hW28+S2pSkRe6uuTShbfgKkulmpBABwQMCspByHbdkqjx+RaIrkfw8Jg88MbZw8NjrbB6QVhzUK1UZIN29YzVET7+mMMllxVJt7XL5fOvkZe71Bin29yGYYlU/UcfMOr8AIY3zB6TGd44e0xM2I8feExolKtFyWfTEhSr0qa90REH7ypzZs9wH0919ZflmhtuUz9avWz1oOurvfWcT6t5uP6VlofHpIQ3zh4eHmOEQLLus7FAUmqg09ob8QXVmR84QT3lkgSJpPziigWyoo+FYRoCtcZBVVgbls5MhG/APTzWHd44e3g0CLbdBPbj97azF9e245f9kAXX7A4WhT1HvJ0XCgV3HGs0ewo7CnLmV6n4eQznHiv4Zcl993inbDJrmrTn09KnYpu34A63J0kYpCTFL1PpM3jWkslqpO/CPCYnvGZ7eDQAjC0/YsFiJYwrgR+3APYj9YANSEiLsWN6FpghJh0/HWmGkPi2trZxsX1nM1dmDw81tOoNsyqsxi9LqtFtUzGc/v7jpbdnlZSrgVw2b4GsUu+ZH83IqNuM+PCc+/vVctdF5uEx6eCNs8fExDjxmMwYm2HFmHFuHjJbcZoXTDy7f3V1dTkDjFH+xje+IRtuuKH7ZSq29nzPe94jP//5z51htjwnM9jKExlhnAOt0oSeM9F96P47y7ZbbuLkVSjV5BeXLZKSM94p98MhGuU2LIl76ODhMVbwxtnDowFgYDG0BAyJedEc8ZAxPHjBlobradOmOcO7xx57yKc//Wn5+te/7u7xk5IY6vPOO09+9rOfvep2n2ON5nrT9R/CYNqa188pfiJSXegO7ZlOPe5oCapFN1C55ba7ZGVXQfpKZWnvmOKM8nowdvFYj+GNs4dHA8AgY1gxxnjKgCOGGe8Zr5pr7pvnjHGbN2+e/OpXv5KPf/zjcsYZZ7h7/FrV3LlzpbOzUxYtWlT3KCc1dPDCJ1LpjFvwBdKptGRVFuViVQ7e/92y7VYbq0DLsqqrTxYvuU1SubaB1dsixdU/4OXhMengjbOHRwNgyhoPF0OKgcVQX3DBBe4cj5npagwzRppfmXr22WfdPa4vvPBCOf/88weNMAvLpk+fLrNmzZIHHnhg8N30eAPlbwawxzW1splUzq3OLpX73CtkuM6mVH54zycdJx3tOenvK8h1N/xSVvYUpLdYllIlFLXpHh6TFt44e3g0AAwwHjKG1Kaz//u//9udY3R5P8o5U7McN910U2fQjz76aDelvcUWW7h8zGBj3JcvXy5z5swZt8a5mWBrTow0rKrE6pGKXCYl/cVA9t/rLTJ7g2luxqGvUJFf3nqn5PN885zwa8E8JjW8cfaYmBhHm5BgODCuGGaMK8AQc25T3QCjTDwGvb+/3y0A4xqjbJ9a/fCHP5Rly5bJiSee6O5NegyIJ5NIqkHO61lSUsmUc6un5pOSVwt85inHuy07+b3n2+/9vTy7ihXyej0gM+C88IGjAycDF3Y6eM/DYwJgwhtnvBM6saEdI51ltGOMC9Cy71wBnS4grhWdq3lsAJ6N7zh4J2+AnE3mBM5N9pZm3YFKvjLACvzU+dMoRRjWnLcVN6L1a3ULovVrcgfIw645p9ykw7vGKAOueb8MonL76U9/6qbEDz30ULcozPIkjU19U9/kSZw9a7A0IHreCKz8AO+fgQTlgp9GAXdZFoFp/SaCpNZ02r17xuTCekbPO/T8qP3eJTOmt0stmZHllaxcvfgOHpdMssJabzew4Rk47rUX0fBfUT3VvPmtDLvPF9JuRABLdbZGhNWDyYFjHO1rOFDHyJoBIEeCyb9VZYBOVJ+GXscJZG06D02OxDVLB8czEsroKFV0/IJpQN7RdXR0uO9FUWQCnQnHOIHC0NHSiPhEhveFTGXiFXGkM4sTVB/vMl0HpQEDAM8YD6651yhoCARo0Tg4510qHh6YOXOm9PT0DDYkS9sM1aIOeaeLPJG1veMlcA9acYIOAL1CnhyXLl3qVltjeDHWI+mXlRNZUFb0hHObDqeOkNl9990nX/rSl+SQQw6Rc88918l3xYoV7vn777/fvZ+2TopnkQMysYHDr3/9a5c/tGzAhLwalQ/6Sz6UG7qU18rQ3d3tyrfu0IFloLqlZ6mwLDX1jCtqgDmm1KqmdQCWrii9dLvc99eX5QfzrpdavlM6MxX50oeOkdntqotqa8sa+gLe6+ckVVNDps/l9Xknj0RWqiq3EDlo4ozSSeq9VJgTJa3Qzn4NIkKO1BN1Tt/COQv2kLsd4wT0WYfwzDPPuL6FurA6QEfipm/tnXrmyBcFtAOu0UF0LU7Qf0Fnn332cdfoIfxDP27aY40Jb5ypKBoNC2223377wQqzzilu4whYdbvbbru5zpPGa51jK5TnoYcecu8tN9hgg1d0xNBvtGM20EAJgDw5hzc6DLD55pu7RgP/pk6cE5qBobxwjeF6+umnZccddxyIjQ/wBn2O6BP833333bL77rsPpHh1kNbkgOHknDzQWTp3QMdz2223yVlnnSU/+MEPHC3S0jGhwwwAoA3fPM/76o9+9KPy9re/fXDwRXrANTRJ2wz9gz40yY/zF1980eVPnTdt4OtURj0xNcpKzc10IzGXe7UmlWpSlocJOfKUj8uLPTr4UD/4rOP2kfNOOUrTaN3ov4J63il9iKFCoB5zxolcZeaMPed1/UnbPHr0O/k1NBP4tuMdd9whe++9t6sL5G2zH3HCBluPPvqok7ktMKQuODarja8J//jHPxz/W2655aAuEKAdN30Gw0899ZTssMMO7hr6Rpd6aIaOj1dENHRiwkZ0dBgG60zpBE2R4grQxYNEaQx2Plz6ZgdgCgsoDw2XYJ10I8EADTpjGgNy5ZqBCIFz4rhHGuMfDJfn2oSh/AB4NRrDPdPsAKI8cU6dj0a+pEUfGUQiIwLeDl4v8QcccIAzzN/61rcGDTNAljxPGuhEZWvGGkNMXtwnnmsbAPAsiJZlXYLRNPrEWT2AoenXNpBXEPJqqn7Uv8588rfGnLSGTC4hU9tETjn+GKn19UhQrsj8hUtkWV8o/dXAfVqFMU6SXL1oJ0O9rqgXHYQFtb1ltf9V9UTQoXoaJTgYhiuXBWD6xuyQ9S0YZltDEGegTpG7tQHiAHGUY2j6ZgcAXdq5XUPXwtD0zQ7M0NDHI38L0AVRPZyMWN3jTFDYe0A6Pas0OhIqzrZEjDPQWDfaaKPBxoPy0BFTBhR6uGeaGVBg6NApE7im4ZoBHe6ZtQnwZIBXAvQAHQcBEGf3DTw7XJ5rE+ABXswwGJ/WWQz3TDMDdKhL6pSyWD1T5/A63DPRgPHkeToYznkGwww/Z599ttx8883yve99b/DzK+iQP/ehjXzRcXjlWe6TF4YCkM7qmXuk52jXVo51DdC0ujV61taoh6Hp1y4weGGwox0+q681jg4J39kdtTljriFdLYscsNc7Zc6MDjXCNVnRU5Err7lZwrR6xmozSI+nrVlqGclQ88rSmZNXRXSYLin1zJ2sHEEe0vCK8vxzQO7Wx7BBDOet0j0CugAtyo3sAfStToZ7ppnBdJDBCH0qdU6ZoN14/Y8ceDVIGeCfYO0AmDwmK9DpCQ1GVoAKo+IMVKRNG8YJOip790igIyYO0Im2AtAzQwl95GBGpFHAkzUMA42GhmqdBOfEGSx9MxqP8QFP8GZ8mozjhtUh9KBv9Uydj6YMyIFODBnRwXFOuOqqq9wuYLxftm+dSQM9kyX5Y9DRY+6bkcfoTp061XVclIX87B7pOdp1o6D8lIf8qAPyhz7x1EOjCAOtWzW2NXRWDWjA9LY7U3mop5tWGSRSKgtVv5yGw/bfSxI1fsVqilx+9Q2ytBsDq+Zc+2t+rQqDTjlLAd6y6qn+ww8PNS9cZr2l8Y6yix9p1T982poSBkRMKyNzZMAgK25YW8ZLRz+gjV60Sv+hQxun3qFNnXNEH5pR/yPB5I38zShTJyDa50xGTHjjTAWhvCgQCgNQJALKjHLHGWg0NF47B9ClTJRhaPpmBxQVpaWDhj50kYk1oOGeWZtgsqUzgi/yJG+jS+Dc6JGGtDzDs8PluTbB6Fk9wyO8Gt3hnmlmoA6hC18A+sSPdloTA0mw53mOTu13v/udu77oooscfxYfrbsHH3zQxZk+mWw5J7Awx8Bz1gbM0+Z6aHnWNpCvgbzhxQwD9TDcM2sT6oCG1qUGztRf1b8a1LulOy6p25zTpp2s9MseO79NttlqE1m2qltW9gey8IY76j9o5bLC2JbV0KuuakR9fgdrrV4Y4mef0KgtHqY8QwOzbxzhnUFStJ9BB4emb3YwQ8xAALrW1rnH9dD0zQ428EMPoW36x71W8M+iQ5M5AX00upMdE944U3FmHKg0gCITqMi4A547Kxg5pxHRgZoStaIM0IN/Go91mqbYw6Vf2wDI17wxGqZ1+mZ4OCeOe6SJduDD5bm2wfgB5Auv8Azvw6VvZrA6hC/oQZ9r6py6j6YdLtCZceR5zgFG/Zvf/KaTGXliTNFdrq3jIS2L3XiWa2hxz+RNfqbvZsApGwFDz3M2qGkkRGVv5aKc3KMsQ9OvS8A1DjWolDTU/xLwfGsD3m0yoXpX7BIpd8tpJx3nVk+rBsplc6+Rnj5XPDW8dY+bVdmpJOtNMPZaX/xKNO43uWqPB0n3J1KGVwsMgOAb+TJQM73mSB0M90wzA3QBbQtA0+qVcg1N3+yAblHf8A5d6twGxa3gn/YHPWsXJgPumWwmKya8caaRWOWZ0gBT3FbAps+t0YBW0Y4CpTXFbRbgyUC+XBufNA7C0HhD9NlGQb7GX6thPBmfYLSvTOjMAM/aOYYWXSUQTwdoIA7AZ/QcOaPrHCkDx6gsLG0UVu5GYXStzEa38fxprxgZ8qkHpeDu6JBA/9Ud3VSagVhRpk/RwUBQkH323FHmbLSBJDNp6ekNZO6Vt7vJcOa1S5U+LVcoBV5SJzCkKttQQ03z5dupevdQx0BfsSbAIyHKN2iWbEeC1Sv0rG+LxrUC8G2DEjBUFnECngnQM35NFiaHyYrJzZ2Hh0dDMIMQG9wnTUxpG/B29Z8z2PWZaJBUg1sq9kguHUqbjo9OPv5IKfV1awedkasXXC89/fW31Sk12NWwKvl0XmoVNe3kQ0joQ7jNr0CdtofHeITXTA8PjzFDqAYT+8vi6XrAMGu3pCHJtLTzlvSaRV9474ma67QO2vet8rqtN9M0oVSqgfzs8iulzHrtZLv09PVLNahJW0a9rdVWfwig67s/j/ELr50eHh5rheZ607wWqZ/RGTljimEWpk2TktFjnV5SsvmB1dG1qkzV26cef7iUSl1SCcqy+ObbZXlfWQo1kamdcySshm7rToM50OGrW2sPj3EFb5w9PDzGDnz7pAbTdUTYzYhBrX/1rNFqVUM10qlMTh3otMaGkqiKHLz3W+R1282RctAnK3oKcuWCX0qYyqmxTkqe9/sDC+YwyrxuDtilxBGIEPHwGKfwxtnDw2Ot0NyFSHVjyRfO7pxvnvCUmd5290VSapCramdLZXYN01j2zlbPuUPDaScfKZlsIJVESuYtvFFWdon0sWeIps+wdi9RU0e8poa5qgZa6dS/qSJbD49xDW+cPTw8xghmKNkfu6phiNFUG13jyyg9rYUpKVcw4gPT3WrAy/0l2Wevd8kGG7ZLOt8m3QWRq+ffJlM79dEKBl4tdKKiuVac8a8PADw8Jga8cfbw8BhTDOuHD0RWB74Nd966etDpdFZS6bTUKiWZ2p6TtmQo55x5cn2zmDApVyxYLC+t1AeYLuc5Nfr8nAaWno08X4lhKXt4jAt44+wxzmDe1NBgsA4V1fXqGzeaO4U9FPWFXwlJqy1Nu/fJwrerLihtDR3tWbcFdjaVlLTG1zdy0ad4/6x6kaoU5fA9d5NZM6dKMpuRFepNX3HNryTMOsdbkVBDXtEn1LDrv/5S0cXXVKUIHh7jFb5385iY4HMbj9gR+3fOrguyoGAsMGQ8wHIwFx0pCpPUIJ9O8QGVnHHaSVIu9UimLS/XLF4iL60QKVfr+aZSGeeB18KaZLJ5qQzwxO9jeHiMV3j19PDwmJBwa7zV4y6qZ3zU/u+R2dPapFbuk97+Prlq0Y0SZNPuXXUySdCkiYSkEhkJamqw6fliH3h4eKw7vHH28PBYK8TvTY8e1VogWbYXrYlccO4ZkgiK7scarr7+RllVECmpIQ7U706l69tP8nFVQo21871rJXf08BiP8MbZw8NjwiKV4rtnNbilohy2906yzRYbqUddkZdX9sncq2+TWjotpSBUD5pfUqoJvx/htmRWa55wn1V5eIxPeOPs4eGxVoh3kdjaI6yWZUZ7Xo8ixx/1PsmkE5LOdcilV18jS7vVV062uY+pkgl+uEMfYDEYP4zBSjPvOXuMU3jj7DEx4b0eD0W1WpFsOiXVcp/kU6EccchusvGs6e51cldvWRYuvkWKmi5MZNQ8p9xX0qgOv1zlvoP28Bin8MbZw8NjQgL/PaeGOaFGNpfN8ouRbuX2WR84Se0unnFSLpm7UFaodS6rWa6peU7gSKtdTmZybusTD4/xCm+cPTwaBBtgAH5THLAgCXBtcaSxcxZUVatV9ytLpLUjIH48YbxNYRvq5QpUllU1ygmpVdXwqlzTanj33WMn2XT2DGnL5aSvWJO5829yhpgfo6xWAmE9WLlSlkSKRWK+C/QYn/Ca6eHRACqVivsheAwuRvb/t3cm4JIUVb4/tde9vdLddtM0m40+hAf4UD5QZERREHADfYiI3YM4A+oMigojPoZ5fiMfKny4j4OiCMi+KSiCA4g4g495I8oDkWEUkH3rhe671F75zi+yzr3RZfV6K6vrVsf/9umIjIyME8vJ+OeJzKxE7MP0/gfii8XiOuSdzWZd3oISCB+NJxwZGXHpgLzxD25sXfTTk9k+rF5MYE3tK/oags6qd8xvbn94+bFSGl0lqXRerrr2Jlk7pmOlebPZtER1xmhIqo1IcwcE9CcCOQdMT/TJj5AYGRsJQxrEIW32QbwvvfSS84jz+bwjXNIgaAjl05/+tAuRefPmyRFHHCGXXXaZK4P8ARtBKnIXMqkUd5PZjC+A3nXkfrLbrktcvF5PyyU/uFqUiyWrXbpmfK1UdGyymSHdG6bAgP5EsMyAgCnAeWxKDgheL9sQNCEkTPrcuXMdWUPMEC778JT3228/ueiii+Tyyy935I3nzLHLly+XCy+8cGKpu9/QT940vx3WaH24OZdVguaF53pDijqzHX/s0VItjUuj1pRbb/25vDQayWitIbPmzpZaQ49zRwUE9CcCOQcETAEQMgQM4eIpA/OYIWT2gaGhIUfM5jF/85vflN/85jfymc98Rt7//vdPkPvFF1/sPOgbb7wxeM4bAZcINSXidCYeA+45s4rBz3JWKjV5xxGvk1ct3VmiWlXWrinLNdffJFEuIyVhtSPjPkMZENCvCOQcEDAFlEolR6J4vixFQxKnnnqqi0PIeMjEIWvCsbEx93DYwoUL5ayzzpJjjjnGedTsg5y33357R+533313S0P/gbr2B9LS4N3lbEGiRlNqrDQoY6f1v2w2JcNZkQ8df5x60Wl1qFN
y=-2x+2
Find the intercepts
y=-5/2-5
(-2,-5)
Solve this system by elimination
-4x -15y = -17
-x + 5y = -13
(8, -1)
Graph the equation y=-3/4x+4.
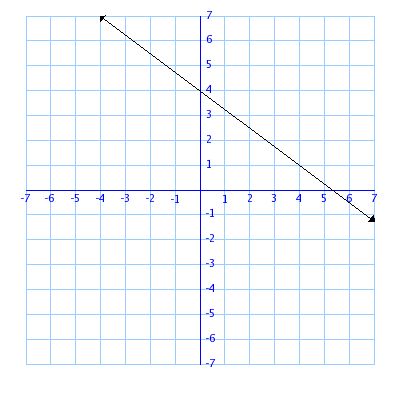
Find the slope that passes through the points (-4,7) and (-6,-4)
11/2
write the slope-intercept form of the equation of the line
11x - 4y = 32y = 11/4x - 8
Find the x and y intercepts for the equation y=-4x-1.
(0,1), (-1/4,0)
solve this equation by substitution
y=5x-7
-3-2y+-12
(2,3)
Find the solution on a graph for the linear inequality
8x - 3y < 12
The points are (0, -4) and (2, 4) and the upper part of the line is shaded.
What is the slope of the equation x-y=-2?
1
A boat travelled 336 downstream and back. The trip took 12 hours. The trip back took 14 hours. What is the speed of the boat?
Boat: 26 MPH
Current: 2 MPHFind the zero of the function from this equation
2x - 4y =12
(6, 0)
Solve the system by elimination.
-2x-9y=-25
-4x-9y=-23
(-1,3)
y>2x-5
The points are (1,0) and (-3,0) the upper part is shaded
Find the slope of the line passing through these two points
(20,8), (9,16)
-8/11
Flying to Kampala with a tailwind a plane averaged 158 km/h. On the return trip the plane only averaged 112km/h while flying back into the same wind. Write an equation to find the speed of the wind and the speed of the plane in still air.
p+w=158
p-w=112
x+2y+-8
(-8,-4)
Find the solution to the system of inequalities
y > -x - 2
y < -5x + 2Two dotted lines with the points (-1, -1) , (0, -2) and (0,2) , (-2,0). The upper half on the first line is shaded and the bottom half is shaded on the second line. The combined shades are in the middle of the two.
Find the slope for y>or = -5/4x+3
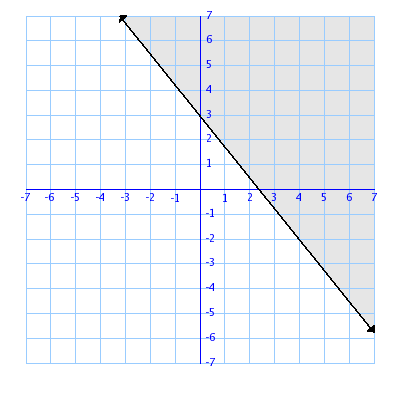
-30+10y=-2x
-15
Write the standard form of the equation of the line through the given point with the given slope
through: (3,5) slope: 5/3
5x - 3y = 0
Find the x and y intercepts for the equation 4x-3y=9.
(0,3), (9/4,0)
solve by using substitution
-3x+3y=4
-x+y=3
no solution
Find the solution on a graph for the linear inequality
y < 6x + 1
The points are (0, 1) , ( 1, 6) , ( -1, -6)
The line is dotted and the bottom section is shaded.