What does the "m" in the equation below represent?
y=mx+b
Slope
What is the domain for the quadratic function below?
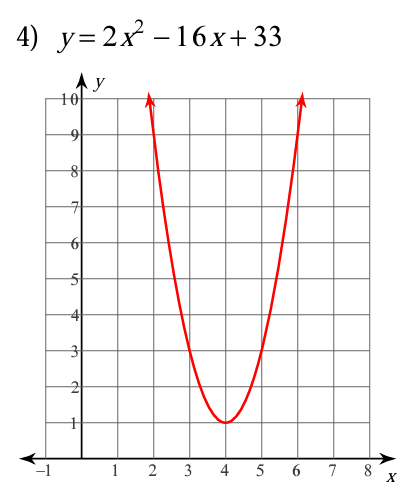
Domain = All real numbers
What is the value of the y-intercept of the graph of
f(x)=12.3(4.9)^x
12.3
y=mx+b
Slope-Intercept form
What is the vertex for the graph below?
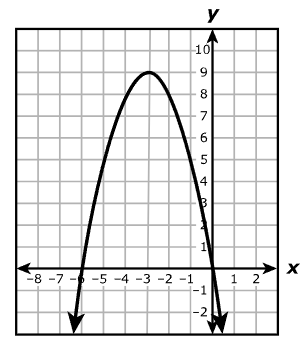
Vertex = ( - 3 , 9 )
What is the slope for the line given? 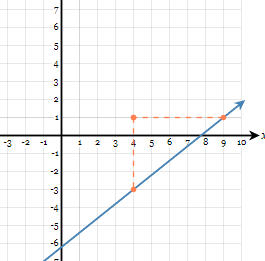
Slope =
4/5
List the other names that can be used to identify the x-intercepts from a quadratic function.
-Solutions
- Roots
- Zeros
What is the percentage of growth for the equation below?
f(x)=150(1.08)^x
Growth % = .08 -> 8%
y=a(b)^x
Exponential Form
How many solutions does the graph below contain?
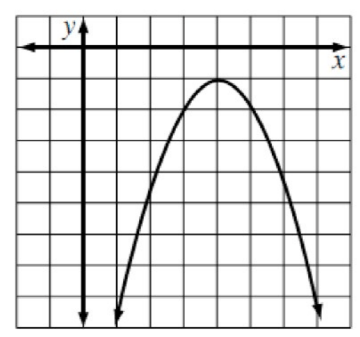
No Solution
Change the equation below into slope-intercept form.
3x+9y=27
y=-1/3x+3
What is the axis of symmetry for the graph below?
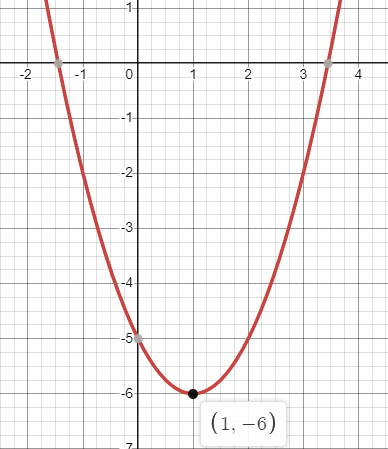
x=1
What is the percent of decay for the equation below?
y=76(0.57)^x
Decay % = 1 - .57 = .43 -> 43%
Ax+By=C
Linear Standard Form
What is the rate of change for the graph below?
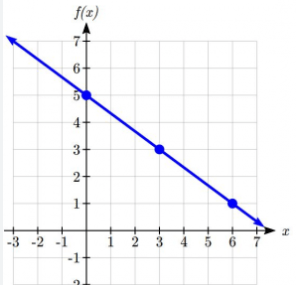
m= -2/3
Identify the type of shading and line needed to graph the equation below. ( hint: change your equation into y=mx+b)
2x-3y>12
Use a dashed line and shade below
y<2/3x-4
Identify the domain and range for the graph below.
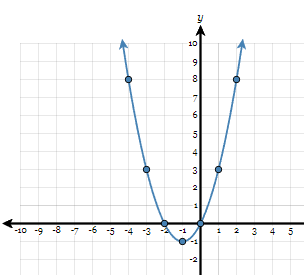
Domain =
All real numbers
Range =
y ≥ - 1
Write the equation in exponential form given the information below:
-There are currently 317 students who play sports.
-This number increases by 4% each year.
Use the growth formula.
y=a(1+r)^x
y=317(1.04)^x
m=(y2-y1)/(x2-x1)
Slope of a line
What are the solutions to the graph below?
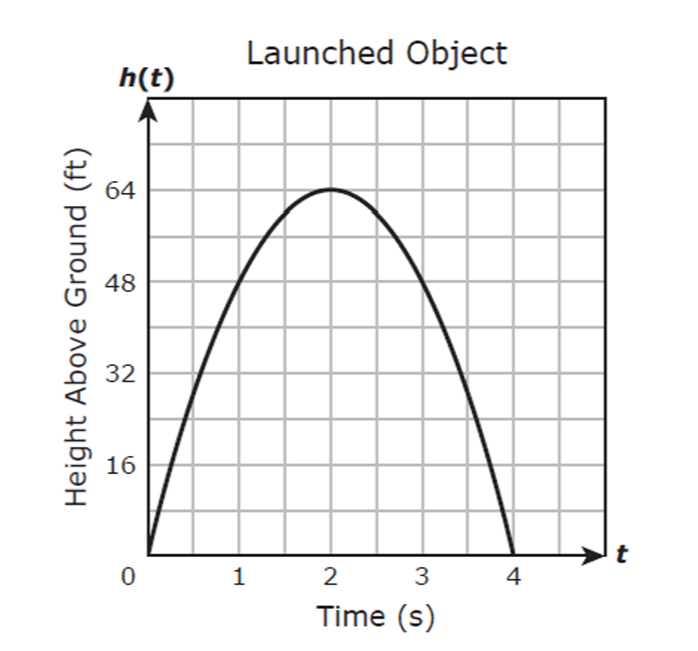
x = 0 and x = 4
Solve the system of equations below.
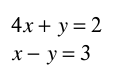
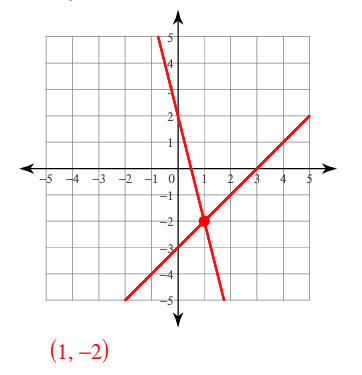
What are the solutions to the function below?
x^2-12=-4x
Write the equation in exponential form given the information below:
-A new computer costs $2100.
-The value of the computer decreases by 25% each year.
Decay formula
y=a(1-r)^x
y=2100(0.75)^x
f(x)=a(x-h)^2+k
Quadratic Vertex Form
What is the range for the graph below?
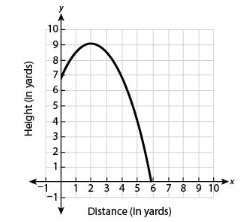
0 ≤y ≤9