Solving
Equations
Equations
Functions
Linear Equations
Slope
Misc
100
Solve: 2x + 2 = 18
x = 8
100
Algebra: Is this a function: {(1, 2), (2, 3), (2, 4)}
No
100
What is the equation for the slope-intercept form of a linear equation.
y= mx + b
100
Find the slope: 2(3x - y) = -10
m = 3
100
What is the zero of a function?
x-intercept
200
Solve the system of equations.
y=3x
5x=2y+1
x = -1
y=-3
200
Algebra: simplify: 3(6wd - 3) + 3wd
Algebra: 21wd - 9
200
Write the following equation in slope-intercept form: 5(x + 2y) = 20
y = -1/2x + 2
200
What is the slope of the following equation:
2x + 2y = 8
slope = -1
200
What values represent the Domain? What values represent Range?
domain: x values
range: y values
300
What is the solution to the system shown below
y=x-4
y=16-x
x = 10
y = 6
300
What is the slope of a line containing the points (-11,5) and (-6,1)?
-4/5 or -1.20
300
Write the following equation in Standard Form:
y=-2/3x+4
2x + 3y = 12
300
What is the slope of the line parallel to 3x+2y=12
-3/2
300
Given f(x)= 6(1-x), what is the value of f(-8)?
54
400
What is the solution to this equation?
2(40 − 5y) = 10y + 5(1 − y)
5
400
Determine the y-intercept of -12x - 8y = 24
(0,-3)
400
What is the Zero of the given Funtion? y= -3/2x-9
(-6, 0)
400
What is the slope of the line x=4
undefined
400
A function is shown.
f(x) = 7 − 4x
What is the value of f(−5)?
27
500
Solve the system of equations:
x + 2y = 27
2x + 3y = 46
x = 11
y=8
500
At a school students are entering at a rate of 21 people per minute. There already are 40 people starting inside the school. Let m represent minutes and n represent number of people in the school.
Make a linear function y=mx+b representing this scenario and find how many people are in the school after 3 minutes.
n=21m+40
n=21(3)+40
n=103 people
500
Write the equation of this graph in slope-intercept form:
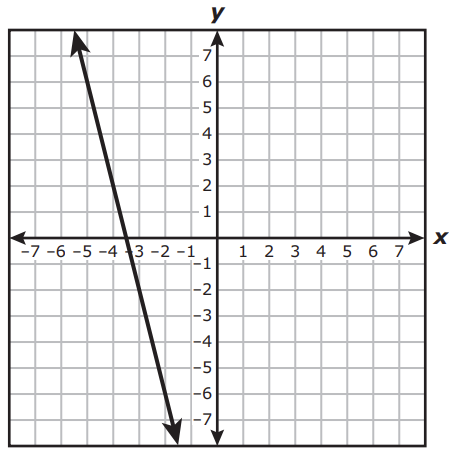
y = -4x -14
500
What's the slope of the line passing through (3,9) (5,4)
slope: -5/2
500
The value of y is directly proportional to the value of x. When x = 512, y = 128.
What is the value of y when x = 64?
y=16