Week 6
Week 7
Week 8
Week 9
Week 10
100
Given the equation -cos(x)-2, determine the period of this equation. (write the word "pi" in answer if necessary)
2pi
100
Find the magnitude of the vector <5,4> (Write square root if needed)
square root (41)
100
Assume α is opposite side a, β is opposite side b, and γ is opposite side c. If possible, solve the triangle for the unknown side. Round to the nearest tenth. (If not possible, enter IMPOSSIBLE.)β = 56.3°, a = 10.6, c = 16.3
13.6
100
A man starts walking from home and walks 4 miles east, 4 miles southeast, 7 miles south, 6 miles southwest, and 2 miles east. How far has he walked?
23
100
Convert the given polar coordinates to Cartesian coordinates.
(12,0)
(12,0)
200
Find y (2pi/3, y) given the equation cos(3x)+4 (write the word pi in answer if necessary)
5
200
Find the magnitude of the vector <2,9> (Write "square root (x)" if needed)
square root (85)
200
find angle a given the following lengths( round answer to the nearest whole number)
a =12
b =19
c =15
43
200
Find all exact solutions on [0, 2π). (Enter your answers as a comma-separated list.) (enter "pi" for pi if necessary)
2 tan2(t) = −3 sec(t)
2pi/3 , 4pi/3
200
Convert the given Cartesian equation to a polar equation. (Use the following as necessary: r and θ.)(Write out "theta" if necessary)
x^2 + y^2 = 7y
r = 7 sin(theta)
300
Find a function that models the simple harmonic motion having the given properties. Assume that the displacement is at its maximum at time x = 0.
amplitude 20 ft, period 1 min
y = 20 cos(2 pi x)
300
Find the area of the triangle with the given measurements. Round your answer to the nearest tenth. Assume α is opposite side a, β is opposite side b, and γ is opposite side c.
a = 4, b = 15, γ = 39°
18.9
300
Find the area of a triangle with sides of length 15 in, 20 in, and 30 in. Round to the nearest tenth.
133.3
300
Find all exact solutions on [0, 2π). (Enter your answers as a comma-separated list.)
2 cos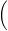
pi/7 θ
= square root (2)
7/4
300
What is the name of the shape the following equation graphs.
r^2= 100 cos(2 theta)
lemniscate
400
Find all exact solutions on the interval 0 ≤ θ < 2π. (Enter your answers as a comma-separated list.)
tan(θ) = −1
3pi/4, 7pi/4
400
Find the length of side b with the given measurements. Round your answer to the nearest tenth. Assume A is opposite side a, β is opposite side b, and γ is opposite side c. A = 20°, β = 20°, a = 31
31
400
Points A and B are on opposite sides of a lake. Point C is 89 meters from A. The measure of angle BAC is determined to be 98°, and the measure of angle ACB is determined to be 59°. What is the distance from A to B, rounded to the nearest whole meter?
195.2
400
Find all exact solutions on the interval [0, 2π). Look for opportunities to use trigonometric identities. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
sin^2(x)+cos^2(x)=6
DNE
400
Is one of the pedals from the rose curve on the x-axis using the equation below?
r = sin(7θ)
(yes or no)
no
500
find a sin formula that matches the coordinates below.
(-pi,-1) (pi,5) (3pi,-1) (5pi,5)
3 sin(½ x)+2
500
Two ships left a port at the same time. One ship traveled at a speed of 13 miles per hour at a heading of 330°. The other ship traveled at a speed of 27 miles per hour at a heading of 198°. Find the distance between the two ships after 10 hours of travel. (Round your answer to the nearest mile.)
370
500
A woman leaves home and walks 13 miles east, then 3 miles southwest. How many miles did she walk? (Round your answer to three decimal places.)
16
500
How many pedals are on the rose curve using the following equation below?
r= 6 cos(8 θ)
16