b = 19, c = 7, 𝛼 = 35° FIND THE AREA
38.1 UNITS SQUARED
If 𝛾 = 45.2°, a = 2.89, b = 3.95. Find side c using Law of Cosine.
c = 2.8
If the initial point is (−2, 3) and terminal point is (4, −4) . Write the vector in component form 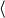 a, b
a, b .
.
⟨6,−7⟩
Given the point, what can be an alternative point?
(-1,-pi/3)
(1,pi3/3) or (1,-pi4/3)
Find the solution.
2cos(pi/5theta)=sqrt3
theta=5/6
Find angle A when a = 24, b = 8, B = 28°
DNE
a = 41, b = 18, c = 33, Find angle A.
Angle A = 103 degrees
If the initial point is (−8, 3) and terminal point is (7, 9), write the vector using the term i and j
v = 15i+6j
Based on the image below. What is the polar coordinate?
(1,pi2/3)
Find all the solutions
cos(2x)+cos(x)=0
x=pi/3,pi,pi5/3
If A = 63 degrees, B = 19 degrees, and a = 2.4, find b to the nearest tenth using the Law of Sines
.9 UNITS
Use the Law of Cosines to find the unknown side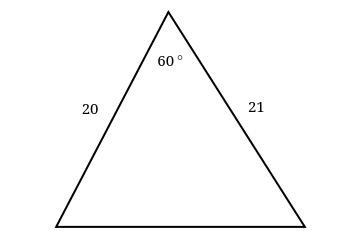
Unknown side = 20.5
Based on the graph, write the vector in component form.
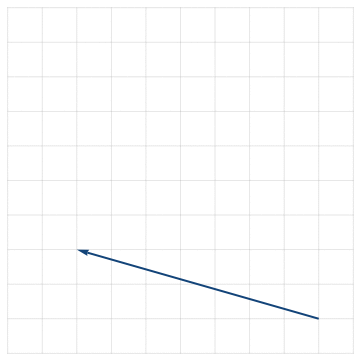
⟨−7,2⟩
Convert this equation to polar form.
x^2+(y-2)^2=4
r=4sin(theta)
Find all the solutions
sin^3(x)=sin(x)
x=0,pi/2,pi,pi3/2
If A = 50 degrees, b = 10, and a = 14, find C to the nearest degree using the Law of Sines.
97 DEGREES
B = 86°, a = 4.6, c = 8.6, Solve all components of the triangle.
Angle A= 28.9 degrees
Angle C= 65.1 degrees
Side b= 9.5
Find the horizontal component when the magnitude is 6 pounds and is pointed in the direction 12 degrees above the horizontal.
5.87 pounds
Convert this equation to rectangular form.
r=3sin(theta)
x^2+(y-3/2)^2=9/4
Find all solutions (hint: it is not a exact solution)
7sin^2(x)+sin(2x)sec(x)-6=0
x=.9172,2.2243
b = 4.1, c = 6.9, 𝛾 = 80° SOLVE THE TRIANGLE
angle a= 64.2 degrees, angle b=35.8 degrees, side a= 6.3
Using the image below, find all the missing angles.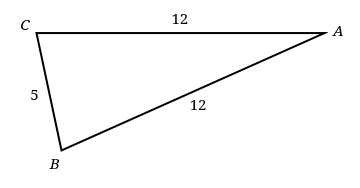
Angle A= 24 degrees
Angle B= 77.5 degrees
Angle C= 78.5 degrees
Find the magnitude and direction of the vector
<3,8>
magnitude=
sqrt73
direction=
𝜃 =tan-1
(8/3)
Based on the graph, what type of shape is this? What is the equation?
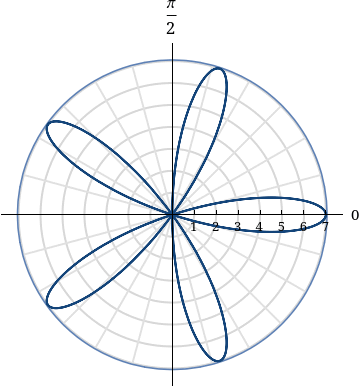
Rose curve,
r=7cos(5theta)
Find all the solutions
cos^2(x)(1-cos^2(x))+sin^2(x)(1-cos^2(x))=0
x=0,pi