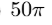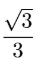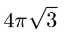Algebra/Number Theory
Geometry
Probability & Combinatorics
Miscellaneous
100
Cagney can frost a cupcake every 20 seconds and Lacey can frost a cupcake every 30 seconds. Working together, how many cupcakes can they frost in 5 minutes?
2012 AMC10A #1
100
What is the largest number of solid 2 by 2 by 1 blocks that can fit in a 3 by 2 by 3 box?
2017 AMC10B #6
100
How many ways can a student schedule 3 mathematics courses -- algebra, geometry, and number theory -- in a 6-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)
2018 AMC10A #4
100
In a magical swamp there are two species of talking amphibians: toads, whose statements are always true, and frogs, whose statements are always false. Four amphibians, Brian, Chris, LeRoy, and Mike live together in this swamp, and they make the following statements.
Brian: "Mike and I are different species."
Chris: "LeRoy is a frog."
LeRoy: "Chris is a frog."
Mike: "Of the four of us, at least two are toads."
How many of these amphibians are frogs?
2010 AMC10 #15
200
What is the greatest number of consecutive integers whose sum is 45?
2019 AMC10A #5
200
A circle has a chord of length 10, and the distance from the center of the circle to the chord is 5. What is the area of the circle?
2018 AMC12B #4
200
How many odd positive 3-digit integers are divisible by 3 but do not contain the digit 3?
2018 AMC12B #15
200
A unit of blood expires after 10! seconds. Yasin donates a unit of blood at noon of January 1. On what day does his unit of blood expire?
2018 AMC10A #3
What is February 12?
https://artofproblemsolving.com/wiki/index.php/2018_AMC_10A_Problems/Problem_3
300
Halfway through a 100-shot archery tournament, Chelsea leads by 50 points. For each shot a bullseye scores 10 points, with other possible scores being 8, 4, 2, and 0 points. Chelsea always scores at least 4 points on each shot. If Chelsea's next n shots are bullseyes she will be guaranteed victory. What is the minimum value for n?
2010 AMC12A #5
300
Three congruent isosceles triangles are constructed with their bases on the sides of an equilateral triangle of side length 1. The sum of the areas of the three isosceles triangles is the same as the area of the equilateral triangle. What is the length of one of the two congruent sides of one of the isosceles triangles?
2014 AMC12A #10
300
Each of the 100 students in a certain summer camp can either sing, dance, or act. Some students have more than one talent, but no student has all three talents. There are 42 students who cannot sing, 65 students who cannot dance, and 29 students who cannot act. How many students have two of these talents?
2016 AMC12A #11
300
What is the value of
2018 AMC12B #7
400
Positive integers 
and 
are such that the graphs of y=ax+5 and y=3x+b intersect the x-axis at the same point. What is the sum of all possible x-coordinates of these points of intersection?
2014 AMC10A #21
400
The figure below shows 13 circles of radius 1 within a larger circle. All the intersections occur at points of tangency. What is the area of the region, shaded in the figure, inside the larger circle but outside all the circles of radius 1?
2019 AMC10A #16
400
When 7 fair standard 6-sided die are thrown, the probability that the sum of the numbers on the top faces is 10 can be written as
where n is a positive integer. What is n?
2018 AMC10A #11
400
Two geometric sequences a1,a2,a3... and b1,b2,b3... have the same common ratio, with a1 = 27, b1 = 99, and a15 = b11. Find a9.
2012 AIME II #2
500
Suppose that real number x satisfies
What is the value of 
?
2018 AMC10A #10
500
Two different points, C and D, lie on the same side of line AB so that triangle ABC and triangle BAD are congruent with AB = 9, BC = AD = 10, and CA = DB = 17. The intersection of these two triangular regions has area m/n, where m and n are relatively prime positive integers. Find m+n.
2019 AIME II #1
500
A fancy bed and breakfast inn has 5 rooms, each with a distinctive color-coded decor. One day 5 friends arrive to spend the night. There are no other guests that night. The friends can room in any combination they wish, but with no more than 2 friends per room. In how many ways can the innkeeper assign the guests to the rooms?
2014 AMC12A #13
500
Suppose that 
and cos a + cos b = 1. What is cos(a-b)?
2007 AMC12A #17