Geometry
Permutations & Combinations
Counting
Probability
Miscellaneous
100
The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?
11/36
100
In how many ways can the letters in BEEKEEPER be rearranged so that two or more Es do not appear together?
24
100
Lola, Lolo, Tiya, and Tiyo participated in a ping pong tournament. Each player competed against each of the other three players exactly twice. Shown below are the win-loss records for the players. The numbers 1 and 0 represent a win or loss, respectively. For example, Lola won five matches and lost the fourth match. What was Tiyo's win-loss record?
000101
100
Jeff rotates spinners P, Q, and R, and adds the resulting numbers. What is the probability that his sum is an odd number?
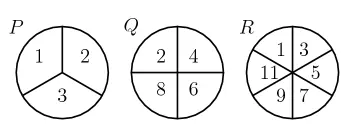
1/3
100
Three friends have a total of 6 identical pencils, and each one has at least one pencil. In how many can this happen?
10
200
The figure below shows a polygon ABCDEFGH, consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that AH=EF=8 and GH=14. What is the volume of the prism?
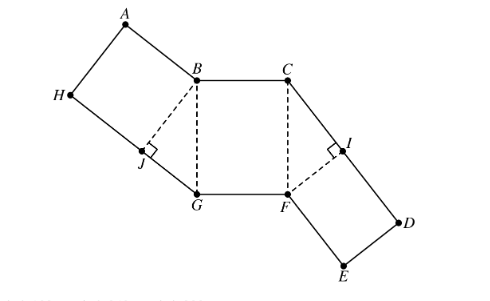
192
200
Alice has 24 apples. In how many ways can she share them with Becky and Chris so that each of the three people has at least two apples?
190 ways
200
The numbers from 1 to 49 are arranged in a spiral pattern on a square grid, beginning at the center. The first few numbers have been entered into the grid below. Consider the four numbers that will appear in the shaded squares, on the same diagonal as the number 7 . How many of these four numbers are prime?
3 numbers
200
Two different numbers are randomly selected from the set {-2, -1, 0, 3, 4, 5}and multiplied together. What is the probability that the product is 0?
1/3
200
Jen has traveled back in time to the 1900s, but he doesn’t know exactly what year it is. He steps out and asks someone, “What year is it?” They reply, “The difference between this year and the last perfect square year is a perfect square. The difference between the next perfect square year and this year is also a perfect square”. Find the year Jen has traveled to.
1961
300
The region shown below consists of 24 squares, each with side length 1 centimeter. What is the area, in square centimeters, of the largest circle that can fit inside the region, possibly touching the boundaries?
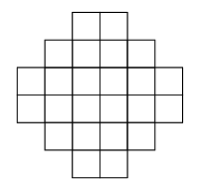
5pi
300
Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?
5760
300
Greta Grasshopper sits on a long line of lily pads in a pond. From any lily pad, Greta can jump 5 pads to the right or 3 pads to the left. What is the fewest number of jumps Greta must make to reach the lily pad located 2023 pads to the right of her starting point?
411 jumps
300
Each square in a grid is randomly filled with one of the 4 gray and white tiles shown below on the right.
What is the probability that the tiling will contain a large gray diamond in one of the smaller grids? Below is an example of such tiling.
1/64
300
In the cube ABCDEFGH with opposite vertices C and E, J and, I are the midpoints of edges FB and HD respectively. Let R be the ratio of the area of the cross-section EFJCI to the area of one of the faces of the cube. What is R^2?
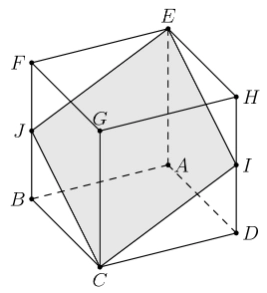
3/2
400
The circle shown below on the left has a radius of 1 unit. The region between the circle and the inscribed square is shaded. In the circle shown on the right, one quarter of the region between the circle and the inscribed square is shaded. The shaded regions in the two circles have the same area. What is the radius , in units, of the circle on the right?
2 units
400
If n is an even positive integer, the double factorial notation n!! represents the product of all the even integers from 2 to n. For example, 8!!=2x4x6x8. What is the units digit of the following sum?
2!! + 4!! + 6!! ... + 2018!! + 2020!! + 2022!!
2
400
In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?
8 ways
400
Imagine a 3x2 grid. How many distinct triangles can be drawn using three of the in this grid below as vertices? (A triangle is only considered distinct if it has its own set of vertices. Size, rotation, and symmetry does not matter.)
18 triangles
400
A regular octahedron has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedron shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of Q?
1
500
Maiya's Favorite Fishing Net (MFFT) is shaped as a regular hexagon of area 6 meters squared. Find the largest possible area of a triangular fish that can fit in her favorite net.
3 meters squared
500
Makayla finds all the possible ways to draw a path in a 5x5 diamond-shaped grid. Each path starts at the bottom of the grid and ends at the top, always moving one unit northeast or northwest. She computes the area of the region between each path and the right side of the grid. Two examples are shown in the figures below. What is the sum of the areas determined by all possible paths?
3150
500
A singles tournament had six players. Each player played every other player only once, with no ties. If Helen won 4 games, Ines won 3 games, Janet won 2 games, Kendra won 2 games and Lara won 2 games, how many games did Monica win?
2 games
500
A cricket randomly hops between 4 leaves, on each turn hopping to one of the other 4 leaves with equal probability. After 4 hops what is the probability that the cricket has returned to the leaf where it started?
7/27
500
Find all values of z such that x^4 - 4z^2 + 3 = 5x^2 - 17
.
z = {2, -2, sqrt5, -sqrt5}