Geometry
Number Theory
Trigonometry
Algebra
Random
100
What is the area of a 30-60-90 triangle where the shortest side is 1?
√3 / 2
100
What is the units digit of 3^100?
1
100
What is sin x if cos x = 4/5?
3/5
100
Simplify log_2 8.
3
100
Let ABCD be a cyclic quadrilateral. If ∠A=80∘and ∠C=2x, find x.
50
200
Angle C and angle BED are right angles. AC = 6 and BC = 8. If DE = 4, find BD.
20/3
200
What is the sum of the roots of the quadratic 2x^2-17x+13?
17/2
200
What type of triangle is it when tan x = 1?
45-45-90 triangle
200
If x + 1/x = 5, what is x^4 + 1/x^4?
527
200
A number is randomly chosen from 1 to 1000 inclusive. What is the probability that it is divisible by neither 2 nor 5?
2/5
300
Triangle ABC has AB = 2 · AC. Let D and E be on AB and BC, respectively, such that ∠BAE = ∠ACD. Let F be the intersection of segments AE and CD, and suppose that △CF E is equilateral. What is ∠ACB?
90 degrees
300
Find the smallest positive integer n such that n = 7 (mod 8) and n = 12 (mod 13)?
103
300
Stella's friends got her a skydiving lesson for her birthday. Her helicopter took off from the skydiving center, ascending in an angle of 37 degrees, and traveled a distance of 2.1 kilometers before she fell in a straight line perpendicular to the ground. How far from the skydiving center did Stella land?
1.677 kilometers
300
Factor x^3 - 6x^2 + 11x - 6.
(x-1)(x-2)(x-3)
300
Rylan’s basketball team has 11 players. How many ways can his coach choose five starting players?
462
400
96
400
What is the product of the roots of the polynomial 3x^3 - 7x^2 + 2x+ 29?
-29/3
400
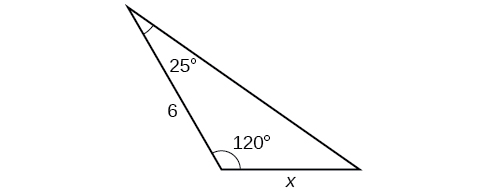
4.42
400
Solve for x where log_3 (x^2-4) = 1.
√7, -√7
400
In cyclic quadrilateral ABCD, ∠ABC=100, ∠BCD=40∘ Find ∠DAB.
140
500
Let ABCD be a cyclic quadrilateral with AB=5, BC=6, CD=7, and DA=8. If AC and BD intersect at point E, find the length of segment AC.
83/11
500
What is the remainder when 7^101 is divided by 11?
7
500
In a triangle ABC, AC=12, BC=13, AB=14. Find cos(∠ACB).
3/8
500
If a + b = 6 and ab = 5, what is a^3 + b^3?
126
500
How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?
45