Polar Coordinates
Polar Conic Equations
Converting Coordinates
Converting Equations
Polar to Rectangular
Polar to Rectangular
Converting Equations Rectangular to Polar
100
What quadrant is the point (4, -2pi/3) located in?
3rd
100
What is the eccentricity of an ellipse?
any number between 0 and 1
100
Convert the polar coordinates (3, pi/2) to rectangular.
(0, 3)
100
rcostheta=16
x=16
100
x^2+y^2=36
r=6
200
What quadrant is the point (-4, -5pi/6) located in:
1st quadrant
200
What is the rectangular equation of the directrix for the polar conic r = 6/(1 - 3cos(theta))
x = -2
200
(3, -pi/6)
Convert from polar to rectangular. Exact coordinates please.
(3sqrt(3)/2, -1.5)
200
r=6
x^2+y^2=36
200
y=10
r=10/sintheta or r=10csctheta
300
Give another set of coordinates for the point
(4, -3pi/4). The angle must be coterminal and positive.
(4, 5pi/4)
300
What is the eccentricity and type of conic for the equation
r = 4 / (5 - 3sin(theta))
3/5, ellipse
300
Convert from rectangular to polar: (-2,7)
Theta must be positive, round to 2 decimal places. Exact radius please.
300
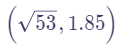
theta=3pi/4
y=-x
300
3x+2y=4
r=4/(3costheta+2sintheta
400
Give two coterminal angles (one positive and one negative) that are pi radians away from 5pi/6.
-pi/6 and 11pi/6
400
What is the polar equation for the parabola with vertex at (4, pi/2)?
r = 8/(1 + sin(theta))
400
Convert the rectangular point (0, 3) to polar coordinates.
Answer in radians!
400
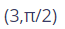
r=2sectheta
x=2
400
(x-2)^2+y^2=4
r=4costheta
500
Where is the point (-2, pi/2) located on the polar coordinate plane? Be specific
2 units directly below the pole.
500
What are the coordinates of the vertices for the polar conic r = 5/(1- 3sin(theta))
(-5/2, pi/2) and (5/4, 3pi/2)
500
Describe the points that have the same coordinates in both the rectangular coordinates and polar coordinates.
Points on the positive x axis.
500
r = 2 / (1 - sin(theta))
Write in standard rectangular form
x2 =4(y + 1)
500
y = x2
r = sin(theta) / cos2 (theta) or
r = tan(theta)/cos(theta) or
r = tan(theta)sec(theta)