Degree of f(x)=7x4+2x3-5x+9.
What is 4?
They are the zeroes of the table below.
x -2 -1 0 1 2 3 4 5
y -18 0 4 0 -6 -8 0 24
What are -1, 1, and 4?
According to the table this is the absolute maximum of this function.
x 1 2 3 4 5 6 7 8
y -24 0 -8 -12 0 16 0 -108
What is (6, 16)?
According to the table, the graph of the polynomial function is doing this on the interval x<-1
x -2 -1 0 1 2 3 4 5
y 8 3 0 -1 0 3 8 15
What is decreasing?
If two values are separated by 8 units, then their product is P(x)=x2+8x. This is the least product those values can possibly have.
What is -16?
It is the minimum possible degree of a polynomial graph that has 5 extrema.
What is 6?
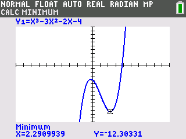 The real zero for this function is closest to this integer.
The real zero for this function is closest to this integer.
What is 4?
According to the table, the ordered pair (0, -8) would be classified as this.
x -2 -1 0 1 2 3 4 5 6
y 24 0 -8 -6 0 4 0 -18 -56
What is a relative minimum?
According to the table, this is the x-interval for which this function is decreasing.
x -2 -1 0 1 2 3 4 5
y -18 0 4 0 -6 -8 0 24
What is 0<x<3?
A store's profit on sunglasses sold in thousands of dollars is modeled by P(x)=-x2+30x-12 where x is the cost of a pair of sunglasses. This is the price that would maximize the store's profit.
What is $15.00
 It is the end behavior of this function.
It is the end behavior of this function.
As x -> 00, f(x) -> 00 and as x -> -00, f(x) -> -00
Based on the following table the zeroes of the function are located in these integer intervals.
x -4 -3 -2 -1 0 1 2 3
y 155 52 -21 -64 -77 -60 -13 64
What are -3<x<-2 and 2<x<3
It is the absolute maximum of f(x)=-4x2+6x-3.
What is (0.75, -0.75)?
This is what the function f(x)=x2+2x-8 is doing for the interval x>-1.
What is increasing?
A store's profit on sunglasses sold in thousands of dollars is modeled by P(x)=-x2+30x-12 where x is the cost of a pair of sunglasses. This is the maximum profit they can earn.
What is $213,000
It is the leading coefficient of f(x)=2x7-5x3-8x9+1.
What is -8?
They are the zeroes of f(x)=3x2-8x-3. Round if necessary.
What are x=-1/3 and x=-3?
This would be the classification of (2, -9) in the function f(x)=-x3+10x2-28x+15.
What is a relative minimum?
This is the interval for which the function f(x)=x3+2x2-8x-2 is decreasing. Round to the nearest tenth.
What is -2.4<x<1.1?
A welder is going to create a box without a lid by cutting a square out of each corner of a rectangular piece of sheet metal with dimensions of 90 cm x 60 cm and folding up the flaps to weld the edges of the box. If x represents the side length of the square he cuts out, this would be the formula for volume in terms of x.
What is V(x)=x(90-2x)(60-2x)
or
V(x)=4x3-300x2+5400x?
It is the maximum number of turning points for a polynomial of nth degree.
What is n-1?
It is the maximum number of real zeroes in an nth degree polynomial.
What is n?
The product of two consecutive odd integers can be represented by P(x)=4x2 -1. This is the minimum possible product of two consecutive odd integers.
What is -1?
This is the term for a function that increases over its whole domain (or decreases over its whole domain).
What is monotonic?
A company knows that if they sell baseball bats for $30, they will sell 850 bats. For every dollar they increase the price, they will sell 5 fewer bats. Let x be the number of $1 increases that the company raises the price of their bats. This is the formula for their profit in terms of x.
What is P(x)=(-5x+1000)(x+30)
or
P(x)=-5x2+850x+30000?