Angle Vocab
Name Angles
Angle Addition
Angle Pairs
Parallel and Perpendicular
100
Name and describe the 4 types of angles
Acute - less than 90 degrees
Right - 90 degrees
Obtuse - 90 to 179 degrees
Straight - 180 degrees
100
Name the rays that form the angle.
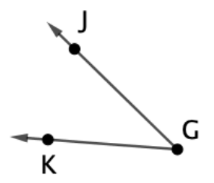
Ray GJ and Ray GK
100
Jesus made a mistake when finding m∠ABC below. Explain his error.
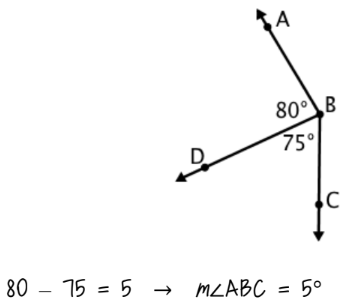
Jesus subtracted when he should have added. Since ∠ABC is made up of ∠ABD and ∠DBC, its measure is the sum of those parts. So m∠ABC should be bigger than 80° and 75°, but Jesus’s answer is not.
100
a. Which diagram shows ∠1 and ∠2 as vertical angles?
b. Explain why the other answer choices are not an example of vertical angles.
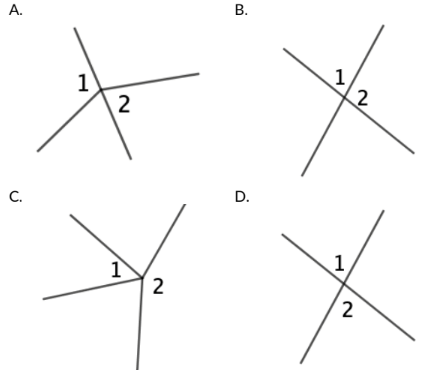
D
Answer choices A and C do not show two intersecting lines, and B shows adjacent angles.
100
Find the opposite reciprocal of each number.
4
3/10
-2
8
-1/4
-10/3
1/2
-1/8
200
Define parallel and perpendicular lines
Parallel - Teo or more lines that never intersect.
Perpendicular - Lines that intersect at a right angle.
200
Name the angle below in three different ways.
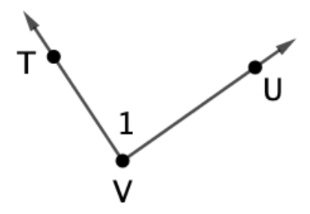
angle TVU
angle UVT
angle V
angle 1
200
If m∠MLR = 23° and m∠KLR = 15°, what is m∠MLK?
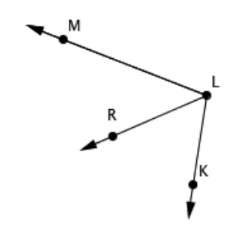
m∠MLK = 38°
200
In the figure below, the measure of angle 4 is 108°. Find m∠1 + m∠3. Explain how you reached your answer.
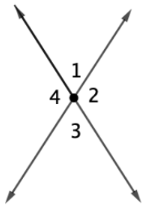
144°
200
Which pair of equations would represent lines that are perpendicular to each other?
a. 2x – 8y = 16
b. 2x + 8y = -16
c. 8x – 2y = -16
a and b
300
Define Complementary, Supplementary, and Vertical angles
Complementary - Two angles whose measurements sum to 90 degrees.
Supplementary - Two angles whose measurements sum to 180 degrees.
Vertical -A pair of opposite angles that form when two lines intersect and are always equal.
300
a. Name the angle below that has vertex T.
b. Why can't we name the angles in this figure using numbers?
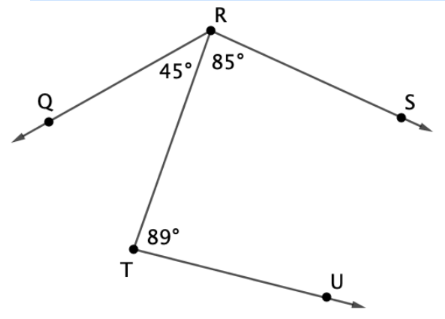
a. angle RTU, angle UTR, or angle T
b. The numbers are angle measurements.
300
The measure of ∠JKL is 125°. Natalie wrote the equation 3x + 5 – 40 = 125 to find the value of x. Is this correct? Explain.
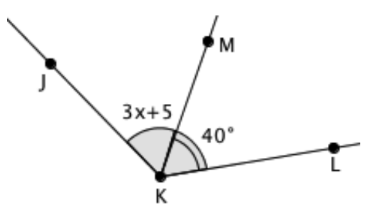
No. She should have added the adjacent angles, since 125 represents the measure of ∠JKL, which is the whole angle the two parts create together.
3x + 5 + 40 = 125
300
In the figure below, all lines intersect at point R with angle measures as marked. Find the measure of ∠LRM.
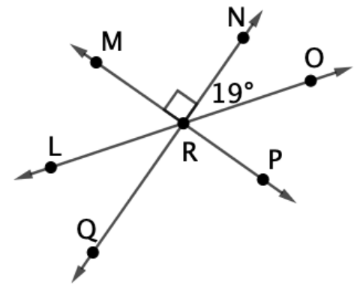
180 – 90 – 19 = 71
m∠LRM = 71°
300
Are the lines parallel, perpendicular, or neither? Justify your answer.
Neither. Counting rise run on the graph or using the points on each line and the slope formula, we see slope m1 = 3/2 and slope m2 = -3/5. These are neither the same (parallel) nor opposite reciprocals (perpendicular).
400
Define opposite rays
A pair of rays that share an endpoint and extend in opposite directions, forming a line.
400
Name ∠RSW without using R or W.
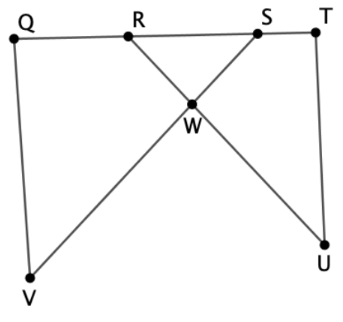
angle QSV or angle VSQ
400
Daniel says that the problem above cannot be solved. Is he correct? Explain your reasoning.
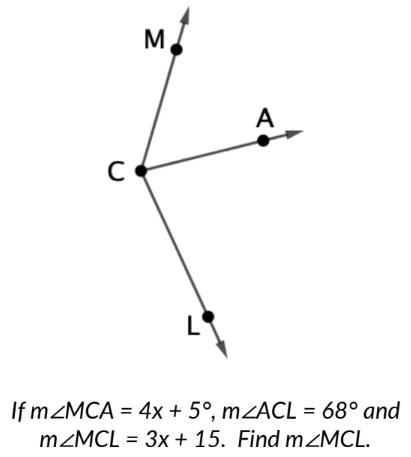
Yes. When you solve for x using the information given, x results in a negative number. When that negative number is plugged in to find ∠MCL, the result is a negative angle, which is impossible.
4x + 5 + 68 = 3x + 15
4x + 73 = 3x + 15
x = -58
m∠MCL = 3(-58) + 12
m∠MCL = -162°
400
Find the value of n.
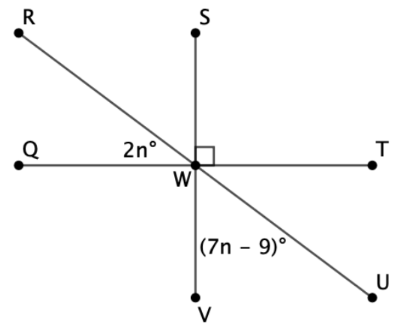
m∠RWS = m∠VWU = (7n – 9)°
2n + 7n – 9 = 90
9n = 81
n = 9
400
Line n goes through the point (7, 10) and is parallel to the line y = 2x + 8. Name another point n passes through.
(6, 8)
(8, 12)
etc.
500
What is being described?
Two angles with a common vertex and side, but do not overlap.
Adjacent Angles
500
Is it possible for two angles to share two common sides but not share a vertex? Explain.
No. Two angles that share two common sides must be the same angle, because the sides will only intersect once. Therefore, they must have the same vertex.
500
The measure of ∠TYW in the figure below is 147°. The measures of the three angles are given in terms of x in degrees. What is the measure of ∠RYW?
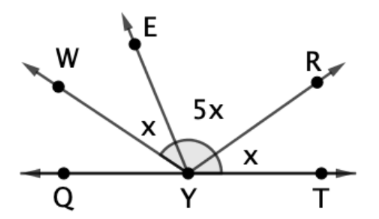
126°
500
Find the values of x and y. Round your answers to the nearest tenth.
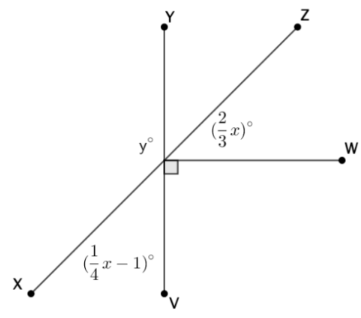
2/3x + 90 + 1/4x – 1 = 180
8/12 x + 3/12 x – 1 = 90
11/12 x = 91
x = 99.3
1/4(99.3) – 1 + y = 180
y = 156.2
500
What is the slope of a line perpendicular to y = 15? Explain.
The slope of y = 15 is 0 so the negative reciprocal would be -1/0, which is undefined. Any line perpendicular to y = 15 would have undefined slope.